Materi Matematika Wajib - Sistem Persamaan Linear Tiga Variabel Kelas 10 MIA - Belajar Pintar
BelajarPintarV3
Peta Belajar Bersama
Hai, Sobat Pintar!
Sebelum kalian belajar tentang Sistem Persamaan Linier Tiga Variabel (SPLTV), coba kalian simak Peta Belajar Bersama ini dulu ya!
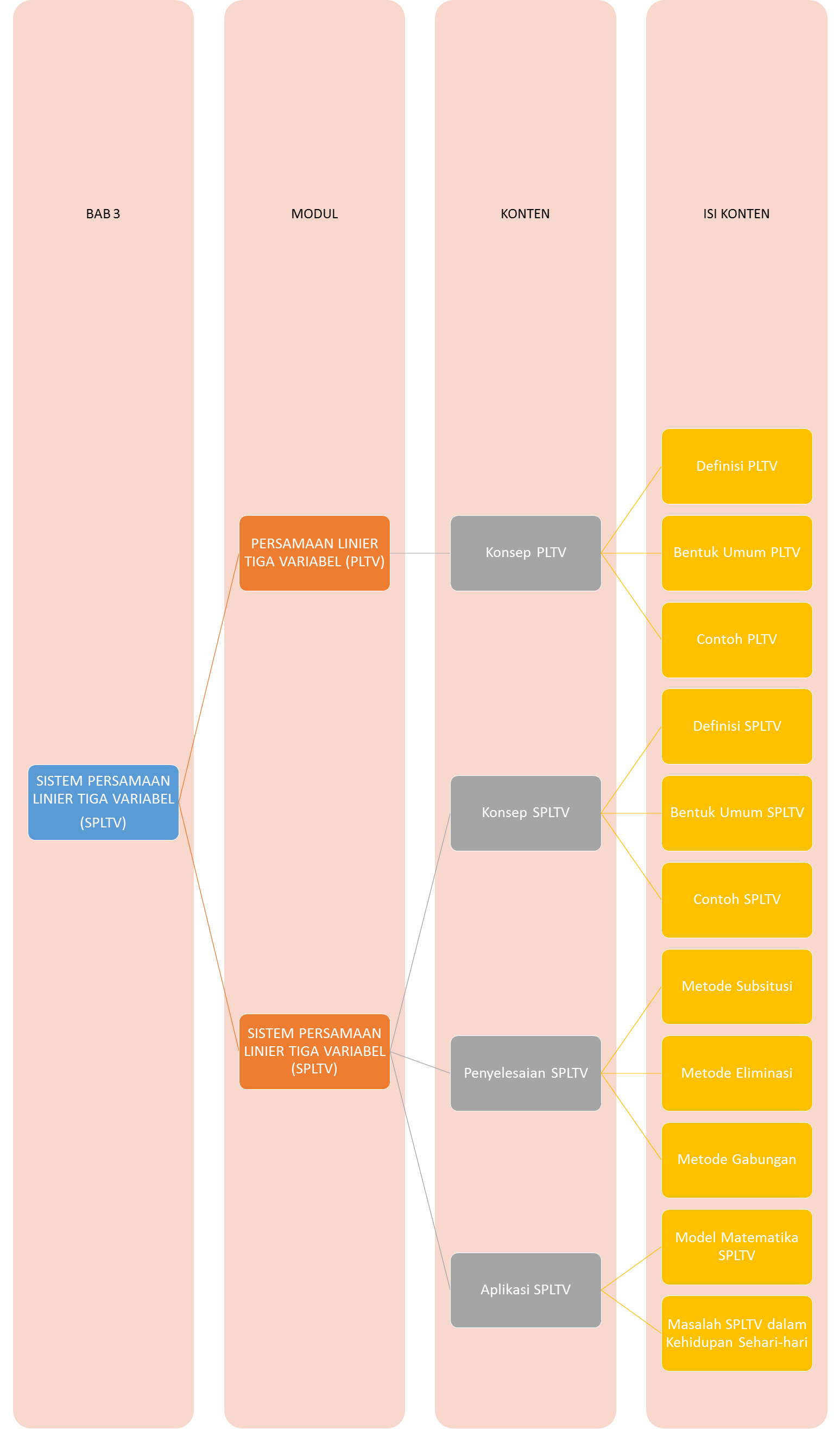
Yuk, mulai belajar bersama !
Konsep Persamaan Linear Tiga Variabel (PLTV)


Sumber : Indonesian.alibaba.com
Halo, Sobat Pintar!
Kalian pasti pernah membeli buku tulis, pensil dan penghapus sekaligus, bukan?
Jika kalian membelinya secara langsung dalam jumlah yang banyak, apakah kalian tahu harga satuan dari buku tulis, pensil, maupun penghapus?
Kalian bisa mencari tahu harga satuannya dengan menggunakan persamaan linear dengan variabel sebanyak 3 macam, yaitu buku tulis, pensil, dan penghapus.
Nah! Kalau kalian ingat mengenai materi SPLDV, materi kali ini hampir sama dengan SPLDV lho, Sobat! Yuk kita belajar tentang Sistem Persamaan Linear Tiga Variabel!
Konsep Persamaan Linear Tiga Variabel
Persamaan Linear Tiga Variabel merupakan suatu persamaan berderajat satu yang memiliki tiga variabel. Bentuk umum dari persamaan linear tiga variabel yaitu
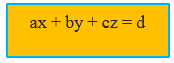
dengan a,b,c,d anggota bilangan real
x, y, z = variabel
a = koefisien dari variabel x
b = koefisien dari variabel y
c = koefisien dari variabel z
d = konstanta
Contoh dari persamaan linear tiga variabel:
- x + 2y – z + 6 = 0
- 5p – 7q + r = 8
- 3a – 2 = b + 9c
Contoh dari Bukan persamaan linear tiga variabel:
- u – 3v = 2u + 1
- 1 - 3k = 2m
- 22j + 32k + 52 = 0
Sistem Persamaan Linear Tiga Variabel

Sistem Persamaan Linear Tiga Variabel (SPLTV) terdiri dari dua atau lebih persamaan linear tiga variabel. SPLTV memenuhi dua syarat : variabel-variabelnya saling terkait dan variabel yang sama memiliki nilai yang sama sebagai penyelesaian dari setiap persamaan pada sistem tersebut.
Bentuk umum dari SPLTV:
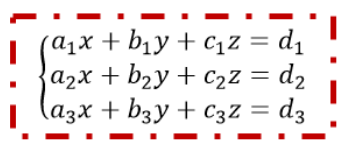
Keterangan :

Contoh dari SPLTV:
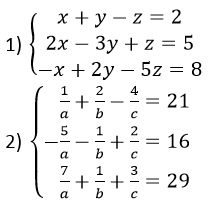
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar adalah perusahaan teknologi informasi yang bergerak dibidang pendidikan, nama perusahaan kami adalah PT. Aku Pintar Indonesia
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved









