Materi Fisika - Dinamika Rotasi dan Kesetimbangan Benda Tegar Kelas 11 MIA - Belajar Pintar
BelajarPintarV3
Peta Belajar Bersama

Yuk, mulai belajar bersama!
Pengertian Dinamika Benda Tegar
A. Pengertian Dinamika Benda Tegar

Buku kelas X anda telah mempelajari tentang dinamika partikel. Dimana suatu benda (dianggap sebagai suatu titik materi) mengalami gerak translasi (bisa lurus atau melengkung) jika resultan gaya pada benda itu tidak nol (F tidak sama dengan 0). Untuk menyelesaikan masalah dinamika partikel, anda harus mahir menggambar diagram benda bebas, kemudian menggunakan F=m.a.
Dalam sub bab ini anda akan mempelajari dinamika benda tegar (benda yang ukurannya tidak diabaikan), dimana resultan gaya dapat menyebabkan gerak translasi dan juga rotasi (berputar dalam poros tertentu). Rotasi disebabkan oleh adanya torsi, yakni ukuran kecenderungan sebuah gaya untuk memutar suatu benda tegar terhadap titik poros tertentu. Tampak ada analogi antara besaran translasi dan besaran rotasi. Gaya F mirip dengan torsi, massa m mirip dengan momen inersia I, dan percepatan linear a mirip dengan percepatan sudut alfa. Ternyata masalah gerak rotasi tertentu seperti menggelinding dapat diselesaikan dengan mudah hukum kekekalan energi mekanik daripada dinamika partikel:
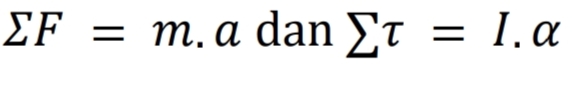
Keterangan:

Pengantar Momen Inersia dan Teorema Sumbu Sejajar

A. Pengertian Momen Inersia
Inersia adalah kecenderungan benda untuk mempertahankan keadaannya naik itu tetap diam atau bergerak. Benda yang sukar bergerak dikatakan memiliki inersia yang besar. Bumi yang selalu dalam keadaan rotasi memiliki inersia rotasi. Jadi, Momen Inersia adalah ukuran besarnya kecenderungan berotasi yang ditentukan oleh keadaan benda atau partikel penyusunnya. Kecenderungan sebuah benda untuk mempertahankan keadaan diam atau bergerak lurus beraturan disebut dengan Inersia.
Inersia disebut juga dengan lembam. Keadaan alami benda ini berkaitan erat dengan hukum I Newton. Oleh karena itu, Hukum I Newton disebut juga hukum inersia atau hukum kelembaman. Momen inersia dari sebuah partikel bermassa m didefinisikan sebagai hasil kali massa partikel dengan kuadrat jarak tegak lurus dari titik poros (r^2). Momen inersia sebuah partikel dirumuskan sebagai berikut:
I=m.r2
Keterangan:
I = Momen Inersia (Kg.m2)
m = Massa (kg)
r = Jari-jari (m)
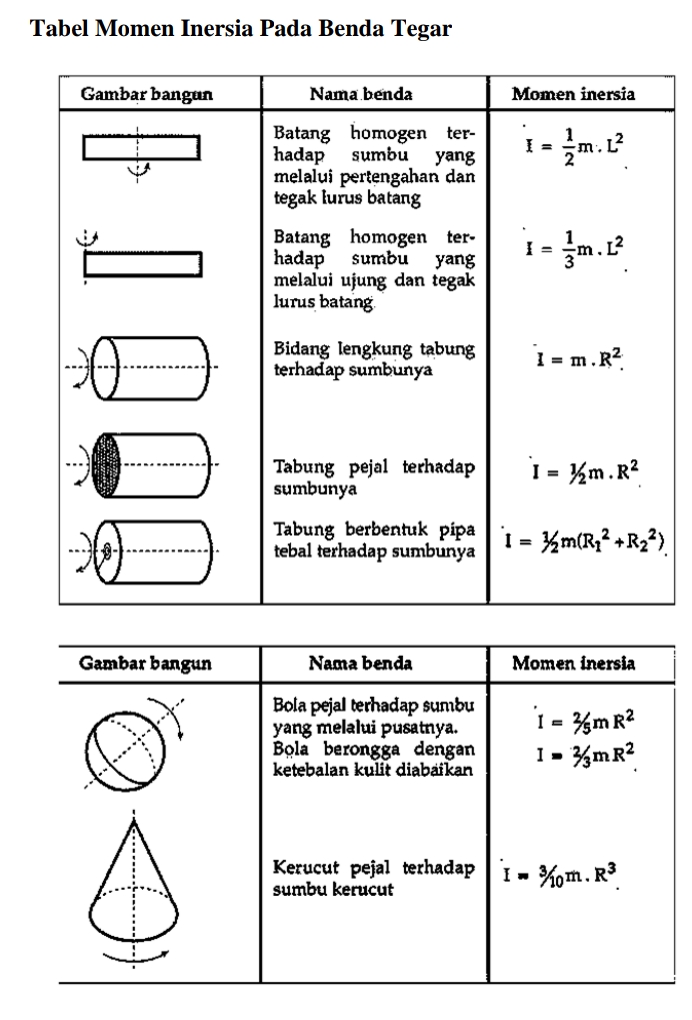

B.Teorema Rumus Sumbu Sejajar
Kita sudah dapat menentukan momen inersia batang bermassa M dan panjang L terhadap poros melalui pusat massanya, yaitu Bagaimana jika kita diminta untuk menentukan Momen inersia ini terhadap poros melalui salah satu ujung batang. Jika momen inersia terhadap pusat massa adalah Ipm maka momen inersia terhadap poros sejajar melalui titik sembarang (titik s), Is ,yang berjarak d dari pusat massa bisa dihitung dengan rumus:
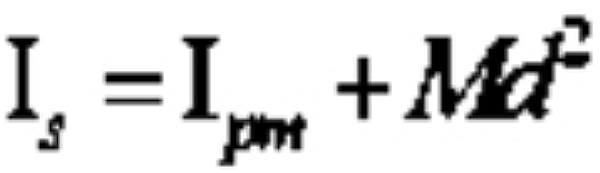
Keterangan:

Pengertian dan Rumus Hukum Kekekalan Momentum

A. Pengertian Hukum Kekekalan Momentum
Anda telah mengenal besaran momentum linear yang dinyatakan oleh p = m.v, pada gerak rotasi, yang analogi dengan momentum linear adalah momentum sudut. Seperti momentum linear, momentum sudut juga merupakan suatu besaran vektor. Arah momentum sudut dari suatu benda yang berputar diberikan oleh aturan tangan kanan. Pada keempat jari yang dirapatkan sesuai dengan arah gerak rotasi, maka arah tunjuk ibu jari menyatakan arah vektor momentum sudut. Momentum sudut dirumuskan:
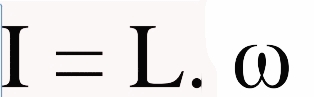
Keterangan:

Kekekalan momentum sudut dapat didemonstrasikan dengan baik oleh seorang penari es.
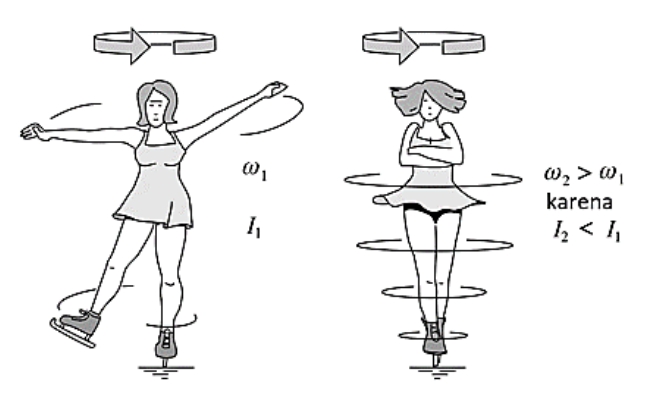
Sumber: Modul Fisika kelas 11 (Doc.Kemdikbud)
Pada gambar di atas penari diperlihatkan memulai rotasinya dengan kedua lengan terentang. Dengan melipat kedua lengannya, penari itu memperkecil momen inersianya terhadap poros (untuk mengecil maka juga mengecil) dan sebagai akibatnya, dia berputar lebih cepat (kecepatan sudut bertambah besar).
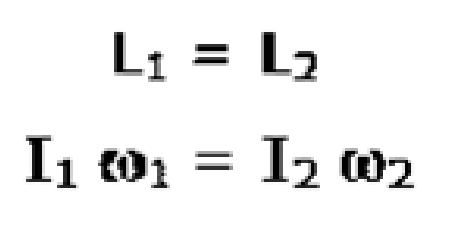
Perbandingan antara energi kinetik sebelum dan sesudah kedua lengan anak direntangkan memberikan hasil bahwa energi kinetik sistem berkurang (tidak kekal). Dapatkah kita simpulkan bahwa pada kasus dimana hukum kekekalan momentum sudah berlaku, hukum kekekalan energi tidak berlaku.
Pengantar Kesetimbangan, Macam-Macam Kesetimbangan Benda Tegar dan Kesetimbangan Partikel

A. Pengertian Kesetimbangan

Korsel gantung dikatakan melakukan gerak rotasi karena lintasannya berbentuk lingkaran dan ada sumbu sebagai pusatnya. Nah sobat pintar, wahana korsel gantung tersebut menerapkan konsep kesetimbangan loh!
Sobat pintar, coba perhatikan tempat duduk para penumpang wahana korsel gantung. Terbuat dari apakah tempat duduk tersebut? Apakah mungkin terbuat dari karet? Jelas tidak mungkin, ya. Jika terbuat dari karet, kemungkinan besar akan putus. Akibatnya, penumpang bisa jatuh. Ini tentunya sangat berbahaya sobat pintar! Itulah mengapa tempat duduk para penumpang terbuat dari logam yang sangat kuat agar menjaga keseimbangan. Para penumpang akan tetap seimbang jika dikenai gaya dari luar. Ingin tahu selengkapnya tentang keseimbangan benda tegar? Simak pembahasan berikut!
Dilihat dari kata yang menyusunnya, kesetimbangan benda tegar tersusun atas dua bagian, yaitu kesetimbangan dan benda tegar. Kesetimbangan menunjukkan suatu keadaan yang berada dalam kondisi setimbang atau seimbang. Sedangkan benda tegar merupakan kata yang digunakan untuk menunjukkan suatu benda yang bentuk atau geometrinya akan selalu tetap meskipun diberikan gaya. Sehingga dapat dikatakan bahwa suatu benda tegar akan mempertahan bentuknya dari pengaruh gaya. Hal inilah yang menyebabkan bentuknya selalu tetap meskipun gaya telah diberikan kepadanya. Jika suatu benda tegar mengalami gerak translasi atau gerak rotasi sekalipun, bentuknya tidak akan mengalami perubahan. Artinya, benda tegar memiliki bentuk tetap.
Maka Kesetimbangan Benda Tegar dapat diartikan sebagai suatu benda yang berada dalam keadaan yang setimbang atau seimbang. Kesetimbangan benda tegar merupakan suatu keadaan dimana momentum sebuah benda tegar bernilai nol.
Adapun syarat yang harus dipenuhi benda tegar agar mencapai kesetimbangan adalah sebagai berikut :
1. Total gaya yang bekerja pada benda sama dengan nol (F = 0)
2. Total momen gaya yang bekerja pada benda sama dengan nol (Torsi = 0)

B. Macam-macam Kesetimbangan
Keseimbangan stabil/mantap adalah keseimbangan suatu benda di mana setelah gangguan yang diberikan pada benda dihentikan, benda akan kembali ke posisi keseimbangan semula. Contoh: Keseimbangan stabil dapat dipandang sebagai keseimbangan yang dimiliki benda jika gangguan yang dialaminya menaikkan titik beratnya (energi potensialnya).
Keseimbangan labil/goyah adalah keseimbangan pada suatu benda di mana setelah gangguan yang diberikan/dialami benda dihentikan, maka benda tidak kembali ke posisi keseimbangan semula, tetapi bahkan memperbesar gangguan tersebut. Contoh: Keseimbangan pada suatu benda dipandang sebagai keseimbangan yang dimiliki benda jika gangguan yang dialaminya menurunkan titik beratnya (energi potensialnya).
Keseimbangan indeferen/netral adalah keseimbangan pada suatu benda di mana setelah gangguan yang diberikan tidak mengubah posisi benda. Contoh : Keseimbangan indiferen dapat dipandang sebagai keseimbangan yang dimiliki benda dimana jika gangguan yang dialaminya tidak menyebabkan perubahan titik beratnya (energi potensialnya).image widgetmage widget
Pengertian dan Rumus Titik Berat

A. Pengertian Titik Berat
Pusat berat/ titik berat adalah suatu titik tempat berpusatnya massa/berat dari benda tersebut.Tinjaulah sebuah benda tiga dimensi berukuran, berbentuk, dan ber massa m sembarang.
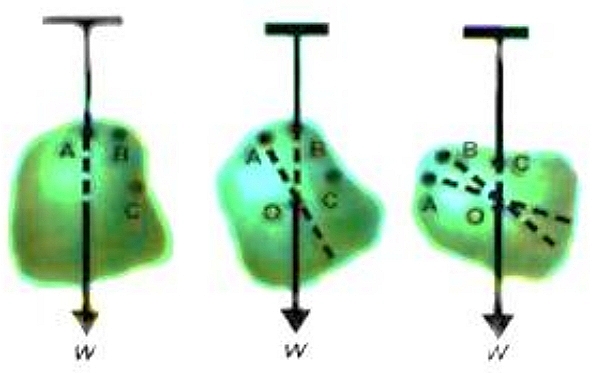
Sumber: Modul Kemdikbud
Jika kita gantung benda tersebut seperti pada gambar di atas, dari sembarang titik seperti A, maka benda akan berada pada kesetimbangan dibawah aksi tarikan pada tali dan resultan W dari gaya gravitasi yang bereaksi pada semua partikel benda tersebut. Resultan ini jelas kolinier dengan tali, dan misalkan kita menandai posisinya.
B. Cara Menghitung Titik Berat
Tabel benda dan letak titik beratnya
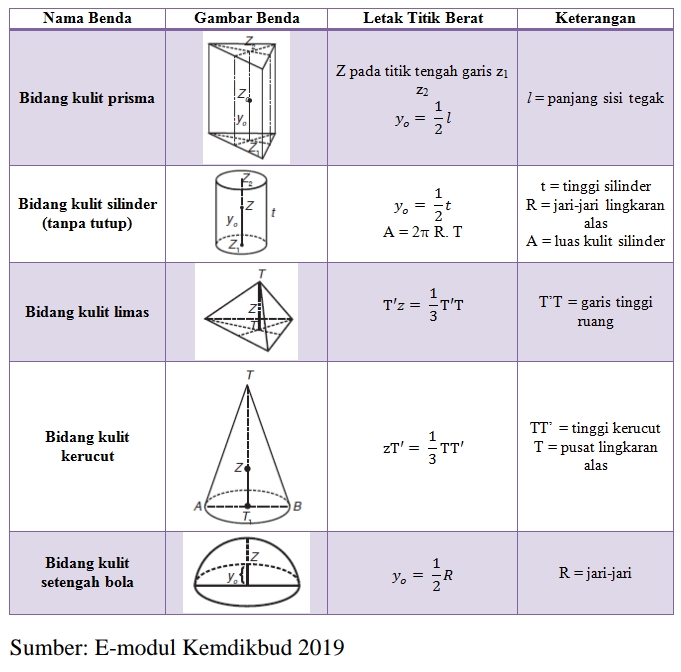
Apabila sistem benda terdiri dari beberapa benda partikel titik digabung menjadi satu, maka koordinat titik beratnya dirumuskan:
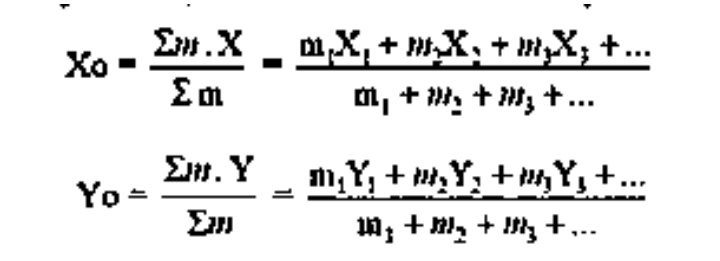
Benda berbentuk garis/kurva: Daftar titik beberapa benda berbentuk garis dapat dilihat dalam lampiran. Apabila sistem benda terdiri dari beberapa benda garis digabung menjadi satu, maka koordinat titik beratnya dirumuskan:
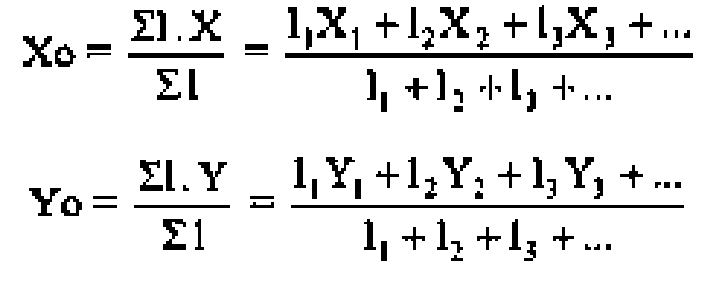
Benda berbentuk luas: Daftar titik beberapa benda berbentuk luas dapat dilihat dalam lampiran. Apabila sistem benda terdiri dari beberapa benda luasan digabung menjadi satu, maka koordinat titik beratnya dirumuskan:
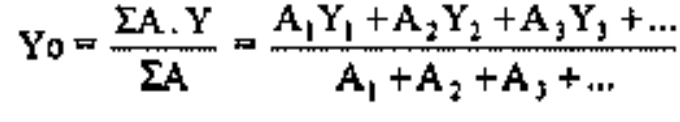
Benda berbentuk ruang/volume: Daftar titik beberapa benda bervolume dapat dilihat dalam lampiran. Apabila sistem benda terdiri dari beberapa benda luasan digabung menjadi satu, maka koordinat titik beratnya dirumuskan:
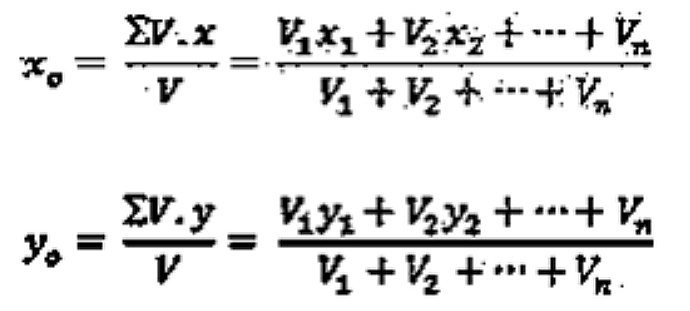
Beberapa contoh penerapan titik berat antara lain permainan akrobat. Ide pada permainanacrobat adalah bagaimana mengatur titik berat gabungan mereka segaris dengan titik tumpu pada lantai (poros). Ini menyebabkan berat total w yang bekerja pada titik berat tidak memiliki lengan momen atau sama dengan nol, sehingga menghasilkan torsi sama dengan nol. Akibatnya sistem seimbang dan pemain acrobat tidak memiliki torsi putar terhadap titik poros yang dapat menyebabkan mereka jatuh ke lantai.
Materi Fisika SMA - 11 MIA Lainnya

Elastisitas dan Hukum Hooke
5 Sub Bab Materi

Fluida Statis
3 Sub Bab Materi

Fluida Dinamis
3 Sub Bab Materi

Suhu dan Kalor
3 Sub Bab Materi

Teori Kinetik Gas
4 Sub Bab Materi

Termodinamika
5 Sub Bab Materi

Karakteristik Gelombang Mekanik
4 Sub Bab Materi

Gelombang Berjalan dan Stasioner
3 Sub Bab Materi

Gelombang Bunyi
4 Sub Bab Materi

Gelombang Cahaya
7 Sub Bab Materi

Alat - Alat Optik
3 Sub Bab Materi

Gejala Pemanasan Global
3 Sub Bab Materi
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar adalah perusahaan teknologi informasi yang bergerak dibidang pendidikan, nama perusahaan kami adalah PT. Aku Pintar Indonesia
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved








