Materi Matematika Minat - Limit Fungsi Trigonometri Kelas 12 MIA - Belajar Pintar
BelajarPintarV3
Peta Belajar Bersama
Halo, Sobat!
Sebelum kita belajar tentang Limit Fungsi Trigonometri, coba kalian perhatikan Peta Belajar Bersama ini dulu, ya!
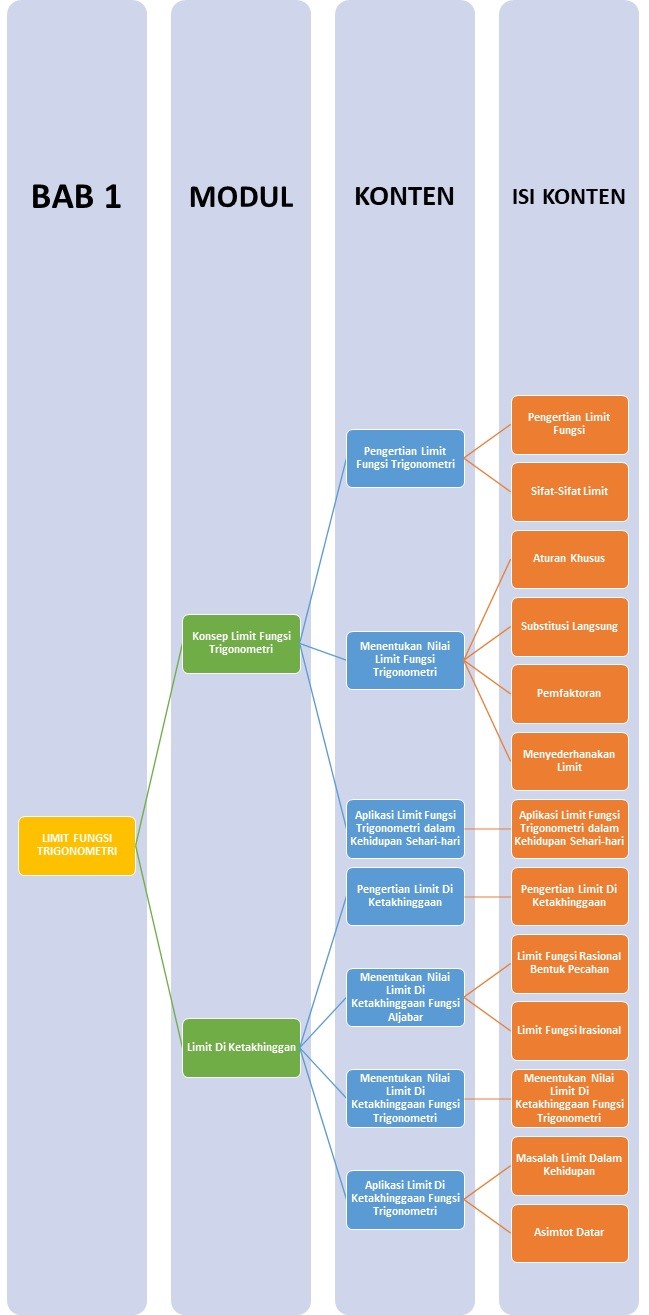
Yuk, kita mulai belajar Bersama!
Pengertian Limit Fungsi Trigonometri

Masih ingat dengan materi limit fungsi yang pernah kalian pelajari saat kelas 11 kemarin?
Nah, masih dalam pokok bahasan limit, kali ini kita akan belajar mengenai limit fungsi trigonometri.
Jadi, fungsinya berupa trigonometri.
Buat sobat pintar yang lupa apa itu limit, akan sedikit dijelaskan pengertian dan konsep umum dari limit suatu fungsi.
Limit memiliki arti mendekati. Oleh karena itu, pernyataan “x mendekati 1” berarti x hanya mendekati 1, tetapi tidak pernah bernilai 1.
Limit secara matematis dapat didefinisikan:
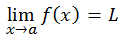
Suatu fungsi dikatakan memiliki limit di titik a jika dan hanya jika limit dari kiri dan limit dari kanan bernilai SAMA, dapat dituliskan:
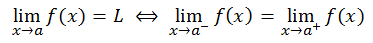
Jika f dan g merupakan fungsi-fungsi yang memiliki limit di c, k = konstanta dan n bilangan positif, maka berlaku sifat-sifat limit berikut:
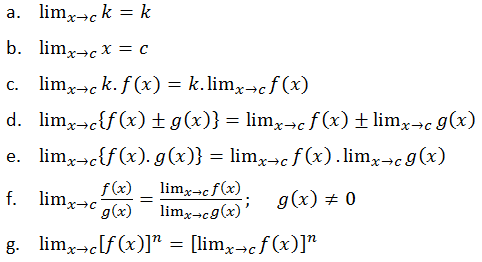
Jadi, limit fungsi trigonometri yaitu limit dari fungsi-fungsi yang memuat perbandingan geometri.
Pengertian Limit di Ketakhinggaan

Kita telah mempelajari limit fungsi untuk suatu nilai yang mendekati bilangan real tertentu, bagaimana jika suatu fungsi didekati dengan tak hingga bilangan?
Nah! Materi kali ini akan membahas mengenai konsep limit di ketakhinggaan.
Suatu limit dikatakan mendekati tak hingga jika dan hanya jika

Catatan:
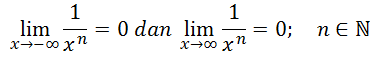
Materi Matematika Minat SMA - 12 MIA Lainnya
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar adalah perusahaan teknologi informasi yang bergerak dibidang pendidikan, nama perusahaan kami adalah PT. Aku Pintar Indonesia
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved









