Belajar Pintar Materi SMP, SMA, SMK

Distribusi Peluang Acak Kontinu

Variabel Acak Kontinu

Sobat pintar sebelumnya sudah tau kan soal variabel acak diskrit?

Berbeda dengan variabel acak diskrit variabel acak kontinu menggunakan bilangan riil untuk menyatakan hasil suatu percobaan.

Variabel acak kontinu diperoleh dari hasil mengukur dan nilainya berupa bilangan riil.

Nilai-nilai variabel acak kontinu jika digambarkan pada garis interval berupa deretan titik-titik yang saling tersambung membentuk garis.

Sebagai contoh hasil pengukuran tinggi badan, hasil pengukuran suhu tubuh, dan lain-lain.

Contoh:
Pada suatu kelas yang beranggotakan 35 siswa dilakukan pengukuran tinggi badan siswa. Dari data hasil pengukuran tinggi badan tersebut diperoleh tinggi badan siswa tertinggi yaitu 175 cm dan terpendek 150 cm. Tentukan variabel acak yang menyatakan hasil pengukuran tinggi badan tersebut!

Pembahasan:
Tinggi badan siswa tertinggi adalah 175 cm dan terpendek adalah 150 cm.
Jika tinggi badan siswa dinyatakan dalam t maka nilainya adalah 150 < t < 175.
Variabel acak t menyatakan tinggi badan siswa. maka T = {t| 150 < t < 175 }.

Distribusi Peluang Variabel Acak Kontinu

Variabel acak kontinu berupa interval bilangan pada garis bilangan riil.

Keempat syarat tersebut harus terpenuhi ya! Jika salah satu dari empat syarat tersebut tidak terpenuhi maka fungsi peluang variabel acak kontinu bukan merupakan fungsi f(x).

Contoh:

Pembahasan:

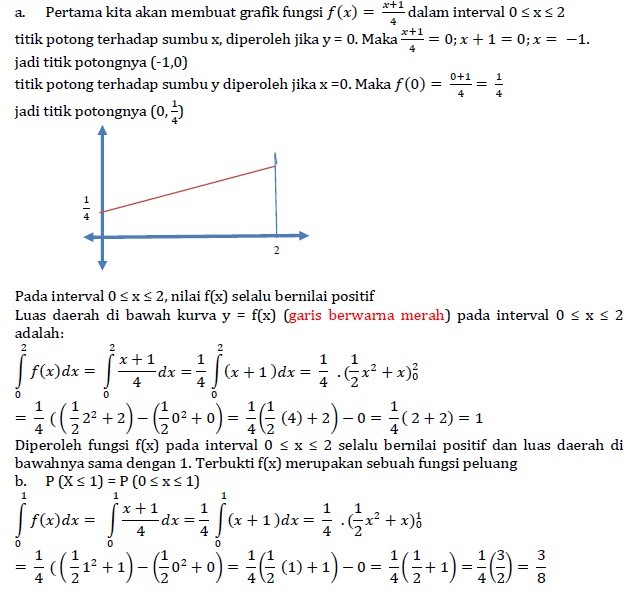
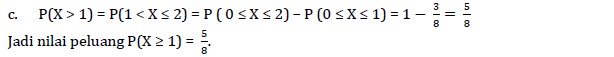
Distribusi Normal

Grafik Distribusi Normal

Pada suatu data frekuensi tertinggi biasanya berada di sekitar nilai rata-rata data (Mean).

Semakin jauh nilai data dari rata-rata (mean), frekuensinya akan semakin rendah.

Misalkan rata-rata data µ sebaran data secara umum dapat digambarkan sebagai berikut:

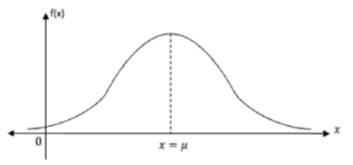
Kurva di atas dikenal dengan nama kurva normal atau kurva lonceng karena bentuknya yang seperti lonceng. Persamaan dari kurva tersebut dinamakan fungsi distribusi normal atau distribusi Gauss.

Fungsi distribusi normal dengan variabel acak X didefinisikan sebagai berikut:

Jika nilai rata-rata = 0 dan simpangan baku = 1 diperoleh distribusi normal baku (standar) yaitu N(0,1).

Rumus fungsi variabel acak Z yang berdistribusi normal baku adalah sebagai berikut:

Nilai Peluang Variabel Acak Berdistribusi Normal Baku N(0,1)

Luas daerah yang dibatasi kurva normal baku N(0,1) dan sumbu mendatar adalah 1.

Hal ini dapat dituliskan sebagai berikut:

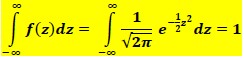
Grafik distribusi normal baku N(0,1) bersifat simetris terhadap garis Z = 0 maka luas daerah di kiri dan kanan garis Z adalah sama, yaitu:

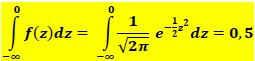
Menghitung luas daerah di bawah kurva normal tidaklah mudah karena harus melakukan pengintegralan terhadap fungsi eksponen.

Misalnya integral berikut untuk menentukan luas daerah di bawah kurva normal baku pada interval Z kurang dari sama dengan z seperti tampak pada gambar di bawah ini:

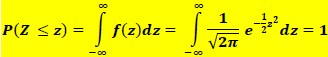
Perubahan bentuk dari normal umum menjadi normal baku dilakukan dengan Langkah-langkah sebagai berikut:

Cari Z_hitung dengan rumus:
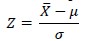
Gambar kurvanya.
Tuliskan nilai Z_hitung pada sumbu x di kurva diatas dan tarik garis dari titik Z_hitung ke atas sehingga memotong garis kurva.
Luas yang terdapat dalam tabel merupakan luas daerah antara garis tegak ke titik 0 di tengah kurva.
Carilah tempat nilai z dalam tabel normal.
Luas kurva normal = 1, karena µ=0 , maka luas dari 0 ujung ke kiri = 0,5. Luas dari 0 ke titik kanan = 0,5.
Luas daerah kurva normal dicari dengan menggunakan tabel kurva normal baku.

Contoh:

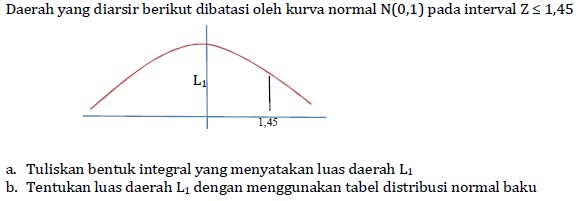
Pembahasan:

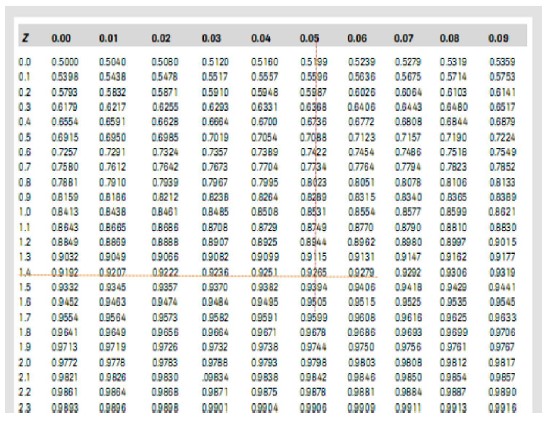
Dari tabel distribusi normal baku diperoleh luas daerah di bawah kurva normal baku pada interval Z kurang dari sama dengan 1,45 adalah 0,9265. Jadi luas daerah L1 adalah 0,9265.

Kerjakan soal berikut dengan benar!

Luas daerah yang dibatasi kurva normal N(0,1) pada interval Z < -0,42 adalah….

A. 0,0567
B. 0,3372
C. 0,5832
D. 0,6628
E. 0,7939

JAWABAN BENAR

0,3372

PEMBAHASAN

Kurva normal N(0,1) pada interval Z < - 0,42 .Lihat gambar tabel z berikut:

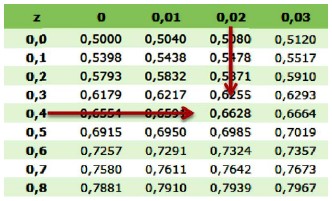
Memeriksa P(Z < 0,42), fokus ke 0,42 = 0,4 + 0,02, periksa “0,4” pada kolom pertama, “z”, dan “0,02” pada baris teratas, dari “0,4” telusuri ke kanan, dari “0,02” telusuri ke bawah, persikuannya didapat 0,6628. Luas (Z < 0,42) = 0,6628.
Luas (Z < -0,42) = 1 – Luas (Z < 0,42) = 1 – 0,6628 = 0,3372.

Kerjakan soal berikut dengan benar!

Dalam suatu perguruan tinggi diperoleh data distribusi berat badan 8500 orang mahasiswa, diketahui mendekati normal dengan mean 53 kg dan deviasi standar 3 kg. Berapa persentase banyak mahasiswa yang berat badannya antara 50 kg dan 55 kg?

A. 33,33%
B. 58,99%
C. 67,89%
D. 89,99%
E. 167,0%

JAWABAN BENAR

58,99%

PEMBAHASAN

rata-rata = 53
simpangan baku = 3
banyak mahasiswa = 8500
Akan dicari P(50 < X < 85) maka
P ( 50 < X < 55 ) = P (X < 55) – P (X < 50)
= P (Z<55 – 53/3) – P (Z<50 – 53/3)
= P (Z < 0,67) – P (Z < -1)
Nilai Z untuk 0,67 adalah 0,7486 dan nilai Z untuk -1 adalah 0,1587 sehingga
= 0,7486 – 0,1587
= 0,5899
= 58,99%