Belajar Pintar Materi SMP, SMA, SMK
BelajarPintarV3
Matematika Minat
Distribusi Peluang
MATERI
Konsep Variabel Acak

Halo Sobat Pintar! Ada yang tau sebelumnya apa itu variabel?
Nah variabel merupakan suatu besaran yang memiliki nilai tidak tunggal, misalnya bilangan asli kurang dari 10, bilangan bulat kurang dari 3, dan waktu tempuh kendaraan.
Jenis variabel ada dua yaitu variabel diskrit dan variabel kontinu.
Variabel diskrit memiliki nilai-nilai yang dapat dihitung, sedangkan variabel kontinu memiliki nilai-nilai yang tidak dapat dihitung.
Variabel acak merupakan variabel yang nilainya ditentukan oleh hasil percobaan, Variabel acak pun sama ada variabel acak diskrit dan ada variabel acak kontinu.
- Variabel acak diskrit diperoleh dari hasil menghitung/membilang, nilainya berupa bilangan bulat.
- Variabel acak kontinu diperoleh dari hasil mengukur dan nilainya berupa bilangan riil.
Contoh soal:
1. Widi melakukan pelemparan sebuah dadu satu kali. Hasil yang mungkin diperoleh Widi adalah....
Pembahasan:
Misalkan X = mata dadu yang muncul sehingga dapat anda nyatakan bahwa X = {1,2,3,4,5,6}.
2. Irwan melemparkan satu keping uang logam sebanyak dua kali. Irwan mengamati banyak hasil angka yang diperoleh adalah….
Pembahasan:
Misalkan X = banyak hasil angka yang diperoleh sehingga X = {0, 1,2}
Fungsi Probabilitas

Distribusi peluang variabel acak diskrit
Nilai pada variabel acak diskrit memiliki peluang.
Peluang nilai variabel acak X dinotasikan dengan f(x)=P(X=x).
Bentuk penyajian peluang nilai-nilai variabel acak diskrit disebut dengan distribusi peluang variabel acak.
Distribusi peluang dapat dinyatakan dalam bentuk tabel, grafik, atau fungsi.
Distribusi peluang disebut juga distribusi probabilitas atau fungsi peluang atau fungsi probabilitas.
Contoh soal:
Diana melakukan pelemparan sebuah dadu. Variabel X menyatakan mata dadu yang muncul.
Pembahasan:
X = mata dadu yang muncul sehingga dapat dinyatakan X = {1, 2, 3, 4, 5, 6}
- Peluang diperoleh hasil mata dadu 1 yaitu f(1)= P (X=1) = 1/6
- Peluang diperoleh hasil mata dadu 2 yaitu f(2)= P (X=2) = 1/6
- Peluang diperoleh hasil mata dadu 3 yaitu f(3)= P (X=3) = 1/6
- Peluang diperoleh hasil mata dadu 4 yaitu f(4)= P (X=4) = 1/6
- Peluang diperoleh hasil mata dadu 5 yaitu f(5)= P (X=5) = 1/6
- Peluang diperoleh hasil mata dadu 6 yaitu f(6)= P (X=6) = 1/6
Distribusi peluang kumulatif variabel acak diskrit
Peluang variabel acak X yang lebih kecil atau sama dengan suatu nilai x, ditulis dengan F(x) = P (X=x).
Nilai F(x) tersebut dinamakan peluang kumulatif.
Misalkan x = c merupakan salah satu nilai variabel acak X yang memiliki peluang F(x), maka nilai F(c) dinyatakan dengan :
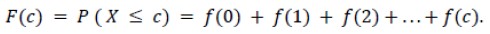
Contoh soal:
Farhan melakukan pelemparan sebuah dadu. Variabel X menyatakan mata dadu yang muncul. Tentukan nilai dari
a. F(1)
b. F(3)
c. F(5)
Pembahasan:
Ruang sampel dari pelemparan sebuah dadu adalah S = {1, 2, 3, 4, 5, 6}
X = mata dadu yang muncul sehingga dapat dinyatakan X = {1, 2, 3, 4, 5, 6}
a. F(1) = P(X < 1) = f(1) = 1/6
b. F(3) = P(X < 3) = f(1) + f(2) + f(3) = 1/6 + 1/6 + 1/6 = 3/6 = 1/2
c. F(5) = P(X < 5) = f(1) + f(2) + f(3) + f(4) + f(5) = 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 5/6
Sifat-Sifat Distribusi Peluang
Misalkan x adalah variabel acak diskrit yang bernilai x1,x1,x1,…,x1 dan f(x1) merupakan peluang nilai-nilai variabel acak X dengan i=1,2,3,4,…,n maka f(x1) memenuhi dua sifat berikut:
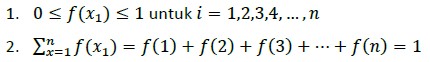
Fungsi Distribusi Binomial

Variabel Acak Binomial
Variabel acak binomial merupakan variabel acak yang nilai-nilainya ditentukan oleh hasil percobaan binomial.
Beberapa syarat pada percobaan binomial sebagai berikut:
- Percobaan dilakukan berulang-ulang.
- Percobaan bersifat saling bebas atau dengan pengembalian. Hasil percobaan yang satu tidak mempengaruhi hasil percobaan yang lain.
- Setiap percobaan memiliki dua macam kejadian yaitu kejadian yang diharapkan disebut sukses dan kejadian yang tidak diharapkan disebut gagal.
- Peluang setiap kejadian tetap dalam setiap percobaan.
Percobaan binomial dapat diamati melalui percobaan pelambungan uang logam.
Perhatikan contoh berikut!
Raka melambungkan sekeping uang logam sebanyak 3 kali. Pada setiap pelemparan dilakukan pencatatan terhadap sisi angka. Percobaan ini merupakan percobaan binomial dengan alasan sebagai berikut:
- Percobaan dilakukan secara berulang-ulang.
- Percobaan saling bebas.
- Percobaan memiliki dua macam ekjadian yaitu keluar sisi angka atau keluar sisi gambar.
Karena uang logam dilambungkan lagi, maka peluang sisi angka dalam setiap percobaan selalu sama yaitu 1/2.
Fungsi Distribusi Binomial
Telah dibahas tadi bahwa setiap percobaan memiliki dua macam kejadian yaitu sukses dan gagal.
Oleh karena itu jumlah peluang kedua kejadian dalam setiap percobaan akan sama dengan satu karena nilai yang berimbang.
Peluang nilai-nilai variabel acak binomial dapat disusun dalam bentuk tabel atau grafik sehingga diperoleh distribusi peluang variabel acak binomial.
Distribusi peluang variabel acak binomial disebut distribusi binomial. Peluang suatu nilai variabel acak binomial dinamakan peluang binomial.
Secara umum rumus peluang binomial x kejadian yang diharapkan dari n percobaan binomial dinyatakan:

Contoh:
Irwan melakukan latihan tendangan penalti sebanyak 3 kali. Peluang sukses melakukan tendangan sebesar 4/5 . Peluang Irwan mencetak tepat dua gol adalah….
Penyelesaian:
p = peluang sukses mencetak gol, maka p = 4/5
q = peluang gagal mencetak gol, maka q = 1 – p = 1 – 4/5 = 1/5
Tanpa rumus distribusi binomial:
Misalkan M = tendangan masuk dan G = tendangan gagal
Tepat mencetak dua gol yaitu MMG, MGM, GMM
1. Peluang hasil tendangan MMG maka peluangnya = 4/5 . 4/5 . 1/5 = 16/125
2. Peluang hasil tendangan MGM maka peluangnya = 4/5 . 1/5 . 4/5 = 16/125
3. Peluang hasil tendangan GMM maka peluangnya = 1/5 . 4/5 . 4/5 = 16/125
Jadi, peluang Irwan mencetak tepat dua gol yakni 16/125 + 16/125 + 16/125 = 48/125 = 0,384
Menggunakan rumus distribusi binomial:
n = 3
x = 2
p = 4/5
q = 1/5

Fungsi Distribusi Binomial Kumulatif
Peluang paling banyak x kejadian yang diharapkan dinamakan fungsi distribusi binomial kumulatif.
Misalkan x = t, maka peluang paling banyak t kejadian yang diharapkan dinyatakan dengan:

Contoh:
Rudi melakukan latihan tendangan penalti sebanyak tiga kali. Peluang sukses melakukan tendangan sebesar 4/5. Peluang Rudi mencetak paling banyak satu gol adalah….
Penyelesaian:
p = peluang sukses melakukan gol = 4/5
q = peluang gagal mencetak gol = 1/5
Tanpa rumus distribusi binomial:
Misalkan M = tendangan masuk dan G = tendangan gagal
Mencetak paling banyak satu gol MGG, GMG, GGM, GGG
1) Peluang hasil tendangan MGG maka peluangnya = 4/5 .1/5 .1/5 = 4/125
2) Peluang hasil tendangan GMG maka peluangnya = 1/5 .4/5 .1/5 = 4/125
3) Peluang hasil tendangan GGM maka peluangnya = 1/5 .1/5 .4/5 = 4/125
4) Peluang hasil tendangan GGG maka peluangnya = 1/5 .1/5 .1/5 = 1/125
Jadi, peluang Rudi mencetak tepat dua gol yaitu 4/125 + 4/125 + 4/125 + 1/125 = 13/125 = 0,104
Menggunakan rumus distribusi binomial:
n = 3
x = 1
p = 4/5
q = 1/5
Karena diharapkan mencetak paling banyak satu gol artinya bisa 0 gol atau 1 gol.


1.
Kerjakan soal berikut dengan benar!
Hammas mengerjakan 6 soal matematika. Variabel acak X menyatakan banyak soal yang dikerjakan dengan benar. Hasil yang mungkin untuk X adalah….
A. (0,1,2,3,4,5,6)
B. (1,2,3,4,5,6)
C. (0,1,2,3,4,5)
D. (0,6)
E. (6)
JAWABAN BENAR
A.
(0,1,2,3,4,5,6)
PEMBAHASAN
Dari 6 soal yang Hammas kerjakan, maka banyaknya soal yang dikerjakan dengan benar bisa saja salah semua atau benar 0 (nol), atau bisa saja benar 1, atau benar 2, atau benar 3, atau benar 4, atau benar 5, atau bahkan benar semua yaitu 6.
Jadi, jika X = banyak soal yang dikerjakan dengan benar adalah X = (0,1,2,3,4,5,6 )
2.
Kerjakan soal berikut dengan benar!
Udin mengerjakan 10 soal dengan pilihan jawaban benar dan salah. Peluang Udin menjawab dengan benar sebanyak 6 soal adalah….
A. 0,1816
B. 0,2051
C. 0,2672
D. 0,3145
E. 0,3264
JAWABAN BENAR
B.
0,2051
PEMBAHASAN
n = 10 ( banyak soal )
x = 6 ( soal yang diharapkan benar )
p = 1/2 ( pilihan jawaban benar )
q = 1/2 ( pilihan jawaban salah )
Peluang Udin menjawab benar sebanyak 6 soal dapat dinotasikan dengan P(B=6), dimana
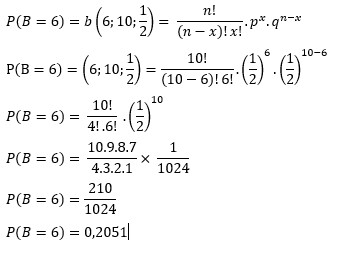

Oops!!!
Yah, jawaban kamu meleset nih. Ingin melihat pembahasan soal ini?

BENAR!!!
Selamat!
Jawaban kamu benar. Ingin lihat pembahasan soal ini?
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved

