Belajar Pintar Materi SMP, SMA, SMK
BelajarPintarV3
Matematika Minat
Limit Fungsi Trigonometri
MATERI
Pengertian Limit Fungsi Trigonometri

Masih ingat dengan materi limit fungsi yang pernah kalian pelajari saat kelas 11 kemarin?
Nah, masih dalam pokok bahasan limit, kali ini kita akan belajar mengenai limit fungsi trigonometri.
Jadi, fungsinya berupa trigonometri.
Buat sobat pintar yang lupa apa itu limit, akan sedikit dijelaskan pengertian dan konsep umum dari limit suatu fungsi.
Limit memiliki arti mendekati. Oleh karena itu, pernyataan “x mendekati 1” berarti x hanya mendekati 1, tetapi tidak pernah bernilai 1.
Limit secara matematis dapat didefinisikan:
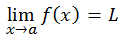
Suatu fungsi dikatakan memiliki limit di titik a jika dan hanya jika limit dari kiri dan limit dari kanan bernilai SAMA, dapat dituliskan:
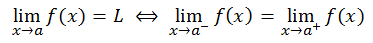
Jika f dan g merupakan fungsi-fungsi yang memiliki limit di c, k = konstanta dan n bilangan positif, maka berlaku sifat-sifat limit berikut:
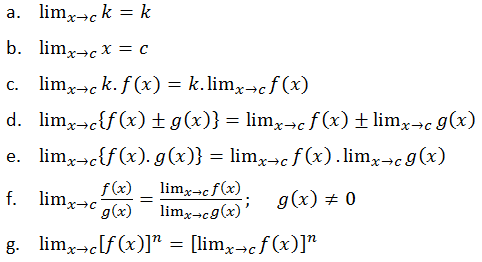
Jadi, limit fungsi trigonometri yaitu limit dari fungsi-fungsi yang memuat perbandingan geometri.
Menentukan Nilai Limit Fungsi Trigonometri

Sobat Pintar, ada beberapa Aturan khusus yang berlaku untuk membantu menyelesaikan masalah limit fungsi trigonometri, diantaranya:
- Nilai Limit Fungsi Sinus
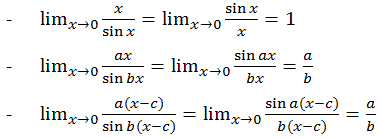
- Nilai Limit Fungsi Tangen
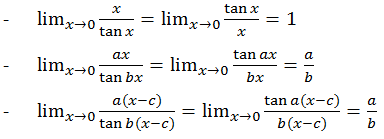
- Nilai Limit Fungsi Sinus dan Tangen
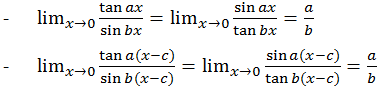
Dalam menyelesaikan masalah limit fungsi trigonometri sama dengan menyelesaikan limit dari suatu fungsi aljabar, yaitu:
- Substitusi langsung : Penerapan metode substitusi langsung dalam menentukan atau menyelesaiakan limit fungsi trigonometri yakni dengan langsung mengganti x dengan angka yang tertera di soal atau
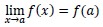
Contoh:
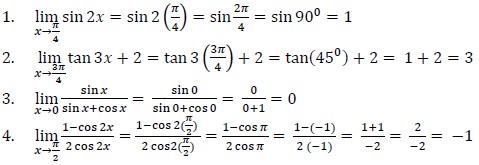
- Pemfaktoran : Penerapan metode pemfaktoran dilakukan ketika kita menemukan jawaban dengan bentuk tak tentu atau (0/0), trik metode pemfaktoran adalah kita harus membuang si pembuat nol dalam fungsi tersebut.
Contoh:
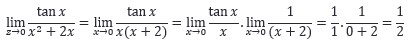
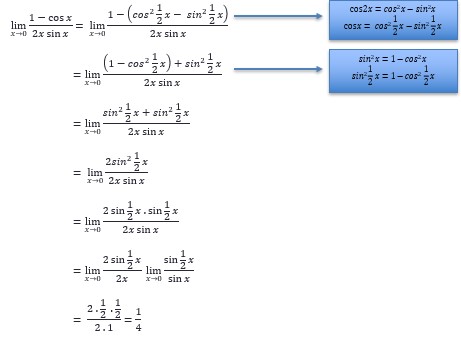
- Menyederhanakannya terlebih dahulu : Jika substitusi nilai yang didekati x ke f(x) menghasilkan bentuk tak tentu (0/0). Selain dengan cara pemfaktoran dapat juga disederhanakan bentuknya dengan menggunakan identitas trigonometri.
Contoh:
Aplikasi Limit Fungsi Trigonometri dalam Kehidupan Sehari-hari


Limit fungsi trigonometri sering diterapkan dalam berbagai bidang di kehidupan sehari-hari, seperti bidang fisika, bidang kedokteran, ataupun bidang astronomi.
Dalam bidang kedokteran, limit trigonometri digunakan untuk mengukur rabun dekat atau rabun jauh dari seorang pasien.
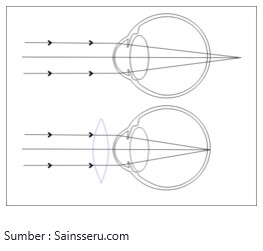
Seseorang yang mengalami rabun jauh akan menggunakan lensa cekung untuk membantunya dalam melihat. Sedangkan seseorang yang mengalami rabun dekat akan menggunakan lensa cembung.
Setelah mengetahui seberapa parah rabun yang diderita pasiennya, dokter akan menentukan jarak fokus lensa cekung maupun lensa cembung pada kacamata yang akan digunakan oleh pasiennya.
Jarak fokus lensa dapat ditentukan dengan menerapkan konsep dari limit trigonometri.
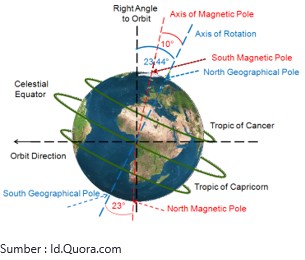
Selain dalam bidang kedokteran, limit fungsi trigonometri juga diterapkan dalam bidang astronomi.Limit trigonometri digunakan untuk menghitung rotasi bumi saat mengelilingi matahari, maupun rotasi bulan saat mengelilingi bumi.
Limit fungsi trigonometri juga dapat membantu ilmuan fisika dalam menghitung gelombang bunyi.
1.
Jawablah soal berikut!

A.

B.

C.

D.

E.

JAWABAN BENAR
E.

PEMBAHASAN
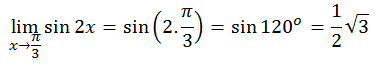
2.
Jawablah soal berikut!
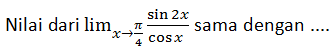
A.

B.

C.

D.

E.

JAWABAN BENAR
A.

PEMBAHASAN
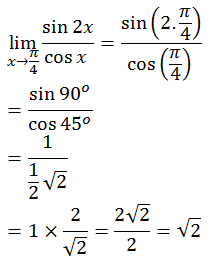
3.
Jawablah soal berikut!
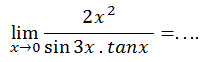
A. -1
B. 0
C. 2/3
D. 1
E. 3/2
JAWABAN BENAR
C.
2/3
PEMBAHASAN
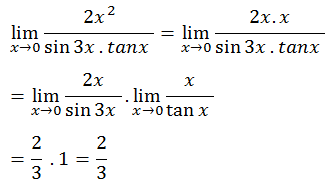
4.
Jawablah soal berikut!
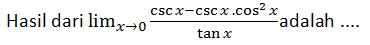
A. 2
B. 1
C. 0
D. -1
E. -2
JAWABAN BENAR
B.
1
PEMBAHASAN
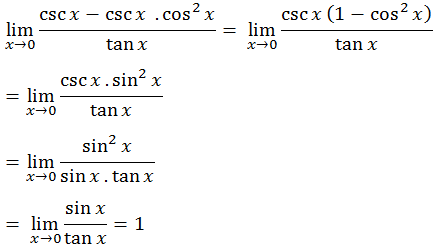
5.
Jawablah soal berikut!
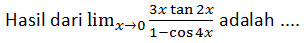
A. 4
B. 3
C. 2
D. 1/2
E. 3/4
JAWABAN BENAR
E.
3/4
PEMBAHASAN

6.
Jawablah soal berikut!
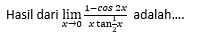
A. 0
B. 1
C. 2
D. 3
E. 4
JAWABAN BENAR
E.
4
PEMBAHASAN
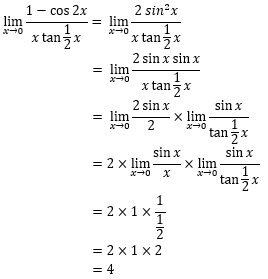
7.
Jawablah soal berikut!
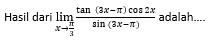
A.

B.

C.

D.

E.

JAWABAN BENAR
B.

PEMBAHASAN
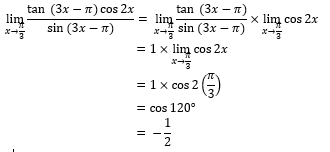

Oops!!!
Yah, jawaban kamu meleset nih. Ingin melihat pembahasan soal ini?

BENAR!!!
Selamat!
Jawaban kamu benar. Ingin lihat pembahasan soal ini?
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved

