Belajar Pintar Materi SMP, SMA, SMK
BelajarPintarV3
Matematika Minat
Turunan Fungsi Trigonometri
MATERI
Persamaan Garis Singgung Suatu Kurva

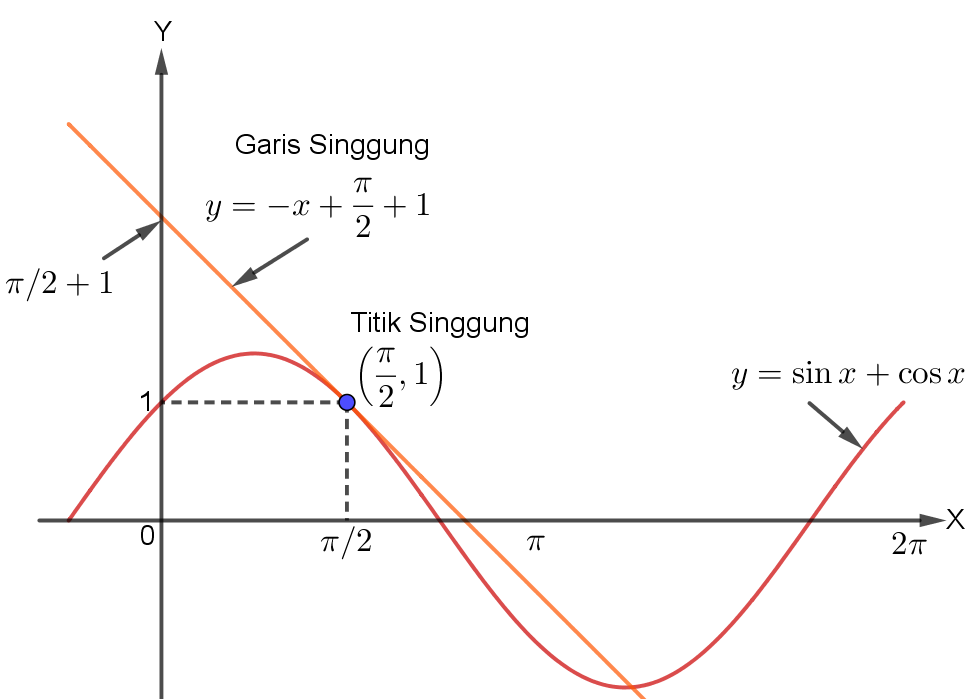
Sumber : mathcyber1997.com
Hubungan turunan dengan kurva fungsi trigonometri hampir sama dengan aplikasi turunan dalam fungsi aljabar lho, Sobat!
Kalian sudah tahu kurva dari fungsi trigonometri, kan?
Nah, berdasarkan kurva-kurva trigonometri, kita bisa mencari tahu persamaan garis singgung, nilai maksimum dan minimum, titik belok, selang kemonotonan, serta selang kecekungan.
Langsung kita bahas aja yuk!
PERSAMAAN GARIS SINGGUNG KURVA
Sobat Pintar masih ingat cara mencari persamaan garis singgung dari sebuah kurva?
Yap! Kita membutuhkan gradien serta sebuah titik singgung pada kurva tersebut untuk mencari persamaan garis singgungnya.
Nah, dalam menentukan gradien dari persamaan garis singgung, kita bisa memanfaatkan aplikasi turunan, Sobat.
Masih ingat tidak ya?
Jadi, gradien garis singgung kurva y = f(x) di titik (x1, y1) adalah m = f’(x1).
Sehingga persamaan garis singgungnyaa adalah y – y1 = m (x – x1).
Pada fungsi trigonometri, konsep untuk mencari gradien dari kurva trigonometri juga sama, yaitu dengan memanfaatkan aplikasi turunan fungsi trigonometri.
Titik Stasioner Fungsi Trigonometri

TITIK STASIONER
Selanjutnya, aplikasi turunan fungsi trigonometri pada titik stasioner.
Titik stasioner (titik belok/titik balik) merupakan suatu titik pada kurva sehingga gradien pada titik tersebut bernilai nol.
Jenis-jenis dari titik stasioner dapat ditentukan dengan memperhatikan tanda pada f’(x), diantaranya:
Titik Balik Minimum
Syarat dari titik balik minimum, yaitu:
- f’(x) bernilai negatif jika x < a
- f’(x) = 0 jika x = a
- f’(x) benilai positif jika x > a
Tanda pada f’(x) berubah dari negatif ke nol, kemudian ke positif.
Perhatikan garis bilangan berikut!
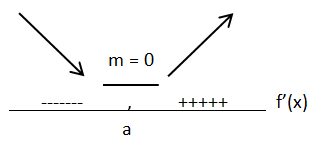
Titik Balik Maksimum
Syarat dari titik balik maksimum, yaitu:
- f’(x) bernilai positif jika x < a
- f’(x) = 0 jika x = a
- f’(x) benilai negatif jika x > a
Tanda pada f’(x) berubah dari positif ke nol, kemudian ke negatif.
Perhatikan garis bilangan berikut!

Titik Belok
Syarat dari titik belok, yaitu:
- f’(x) bernilai positif jika x < a
- f’(x) = 0 jika x = a
- f’(x) benilai positif jika x > a
Tanda pada f’(x) berubah dari positif ke nol, kemudian ke positif lagi
atau
- f’(x) bernilai negatif jika x < a
- f’(x) = 0 jika x = a
- f’(x) benilai negatiff jika x > a
Tanda pada f’(x) berubah dari negatif ke nol, kemudian ke negatif lagi
Perhatikan garis bilangan berikut!
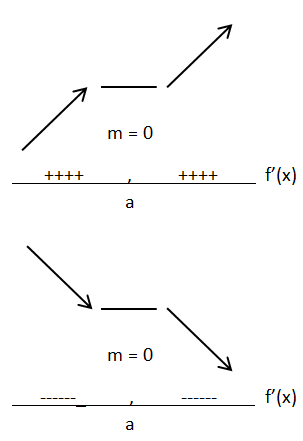
Nilai Maksimum dan Minimum fungsi y = A sin x + B cos x

NILAI MAKSIMUM DAN MINIMUM FUNGSI y = A sin x + B cos x
Nilai maksimum dan minimum dari kurva y = A sin x + B cos x dapat diperoleh apabila mencapai titik ekstrem.
Dalam aplikasi turunan, titik ekstrem dari suatu kurva dapat ditentukan dengan turunan pertama kurva bernilai nol (y’ = 0).
Sehingga diperoleh :
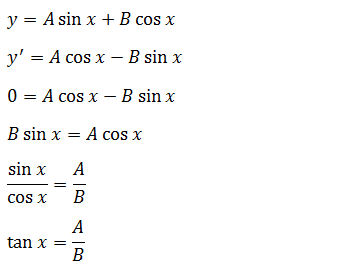
Karena nilai tangen bernilai positif, maka x terletak pada kuadran I atau III.
Sehingga terdapat dua kemungkinan, yaitu : A dan B bernilai positif atau A dan B bernilai negatif.
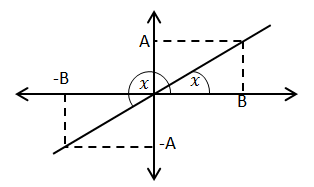
Pada Kuadran I

Pada Kuadran III

Selang Kemonotonan Fungsi Trigonometri

SELANG KEMONOTONAN FUNGSI TRIGONOMETRI
Selang kemonotonan suatu fungsi trigonometri terbagi menjadi dua, yaitu grafik fungsi naik dan grafik fungsi turun.
Dalam hal ini, kenaikan atau penurunan grafik suatu fungsi dapat ditentukan dengan turunan pertama kurva tersebut.
Secara sistematis dapat dituliskan:
- Fungsi f(x) dikatakan naik jika f’(x) > 0
- Fungsi f(x) dikatakan turun jika f’(x) < 0
Selang Kecekungan Fungsi Trigonometri

SELANG KECEKUNGAN FUNGSI TRIGONOMETRI
Selang kecekungan fungsi trigonometri terbagi menjadi dua, yaitu grafik fungsi cekung ke atas atau cekung ke bawah.
Nah, dalam menentukan kecekungan dari suatu fungsi dapat memanfaatkan turunan kedua dari kurva tersebut.
Jika suatu fungsi trigonometri mempunyai turunan kedua pada selang (a,b), berlaku aturan berikut:
- Grafik fungsi f(x) cekung ke atas jika f’’(x) > 0, x berada pada selang (a,b)
- Grafik fungsi f(x) cekung ke bawah jika f’’(x) < 0, x berada pada selang (a,b)
1.
Kerjakan soal berikut dengan tepat!

A.

B.
C.
D.
E.
JAWABAN BENAR
B.
![]()
PEMBAHASAN

2.
Kerjakan soal berikut dengan tepat!
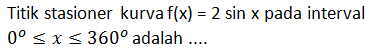
A. (90o, 2)
B. (90o, -2)
C. (180o, 2)
D. (180o, -2)
E. (270o, 2)
JAWABAN BENAR
A.
(90o, 2)
PEMBAHASAN

3.
Kerjakan soal berikut dengan tepat!
Nilai minimum dari fungsi y = 5 cos x – 4 sin x adalah ....
A.

B.

C.

D.

E.

JAWABAN BENAR
B.

PEMBAHASAN
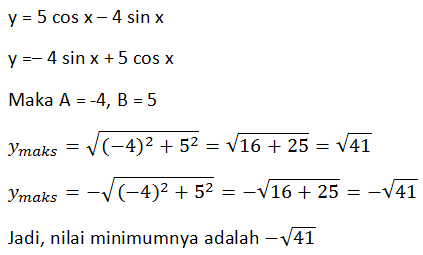
4.
Kerjakan soal berikut dengan tepat!
Pada grafik fungsi f(x) = 7 sin (x – 15), fungsi tersebut akan naik pada salah satu interval berikut, yaitu ....
A. 0o < x < 45o
B. 0o < x < 90o
C. 45o < x < 90o
D. 0o < x < 105o
E. 105o < x < 285o
JAWABAN BENAR
D.
0o < x < 105o
PEMBAHASAN

5.
Kerjakan soal berikut dengan tepat!
Grafik suatu fungsi f(x) = 1 - sin x, akan cekung ke atas pada saat interval ....
A. 0o < x < 90o
B. 45o < x < 180o
C. 0o < x < 180o
D. 90o < x < 270o
E. 180o < x < 360o
JAWABAN BENAR
C.
0o < x < 180o
PEMBAHASAN

6.
Kerjakan soal berikut dengan tepat!
Grafik fungsi f(x) = cos 2x akan naik pada interval….
A.

B.

C.

D.

E.

JAWABAN BENAR
E.

PEMBAHASAN


7.
Kerjakan soal berikut dengan tepat!
Grafik fungsi f(x) = cos2 ( x + 10º ) pada interval 0º < x < 90º adalah....
A. Turun
B. Naik
C. Turun – naik – turun
D. Turun kemudian naik
E. Naik kemudian turun
JAWABAN BENAR
D.
Turun kemudian naik
PEMBAHASAN


Oops!!!
Yah, jawaban kamu meleset nih. Ingin melihat pembahasan soal ini?

BENAR!!!
Selamat!
Jawaban kamu benar. Ingin lihat pembahasan soal ini?
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved

