Belajar Pintar Materi SMP, SMA, SMK
BelajarPintarV3
Matematika Minat
Turunan Fungsi Trigonometri
MATERI
Turunan Fungsi Trigonometri Dasar

Masih ingat dengan materi turunan fungsi yang pernah kalian pelajari saat kelas 11 kemarin?
Nah, masih dalam pokok bahasan turunan, kali ini kita akan belajar mengenai turunan pada fungsi trigonometri. Jadi, fungsinya mencakup perbandingan trigonometri seperti : sinus, cosinus, tangen, cosecan, secan, dan cotangen.
Buat sobat pintar yang lupa apa itu turunan, akan sedikit dijelaskan konsep umum dari turunan suatu fungsi.
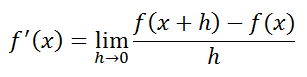
Definisi tersebut dapat digunakan dalam fungsi trigonometri, baik itu fungsi sinus, cosinus, tangen, cosecan, secan, dan cotangen yang akan dijabarkan sebagai berikut.
TURUNAN FUNGSI SINUS
Turunan fungsi sinus dapat ditentukan dengan cara berikut:
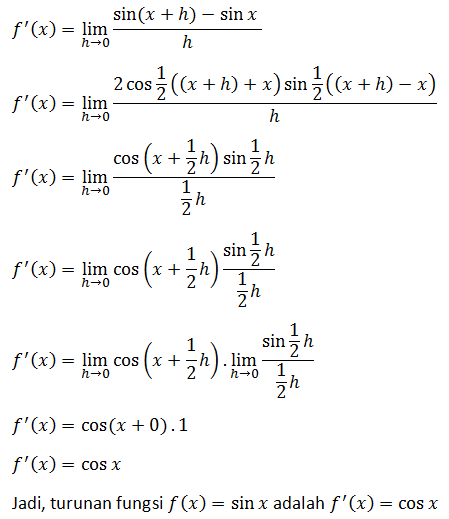
TURUNAN FUNGSI COSINUS
Turunan fungsi cosinus dapat ditentukan dengan cara berikut:
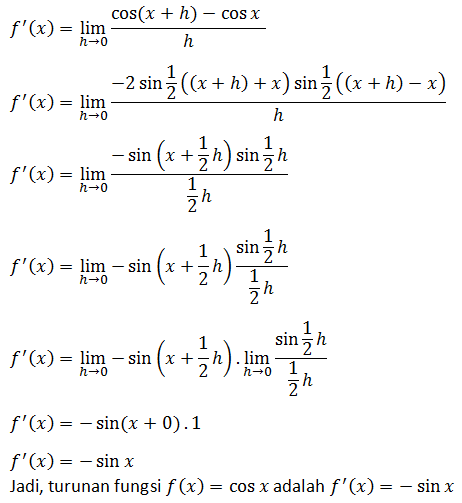
TURUNAN FUNGSI TANGEN

TURUNAN FUNGSI COSECAN
Turunan fungsi cosec dapat ditentukan dengan cara berikut;

TURUNAN FUNGSI SECAN
Turunan fungsi secan dapat ditentukan dengan cara berikut;

TURUNAN FUNGSI COTANGEN
Turunan fungsi cotan dapat ditentukan dengan cara berikut;


Berdasarkan penjabaran di atas, turunan dasar dari fungsi trigonometri, yaitu:

Turunan Fungsi Trigonometri Untuk Sudut ax + b

Oh iya Sobat, Dalam menentukan turunan fungsi trigonometri untuk sudut ax + b dibutuhkan aturan rantai.
Apakah Sobat Pintar masih ingat dengan aturan rantai pada turunan suatu fungsi?
Nah, kalau Sobat belum ingat, akan sedikit dijelaskan mengenai aturan rantai pada turunan suatu fungsi sebagai berikut.
Jika y dinyatakan dalam u, dan u dinyatakan dalam x, maka turunan y terhadap x dapat dinyatakan:
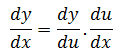
Nah, sekarang akan kita gunakan aturan rantai tersebut untuk menentukan turunan fungsi trigonometri pada sudut ax + b.

Aturan yang sama juga berlaku pada fungsi sinus, cosinus, tangen, cotangen, secan, dan cosecan yang ditunjukkan pada tabel berikut

Turunan Kedua

Jika f fungsi yang terturunkan, maka turunannya f' juga berupa fungsi, sehingga f' boleh jadi mempunyai turunan tersendiri, yang dinyatakan oleh (f')' = f''. Fungsi f'' yang baru ini disebut turunan kedua dari f karena dia berupa turunan dari turunan f.

Contoh:
1. Turunan kedua dari y = x cos x adalah….
Penyelesaian:
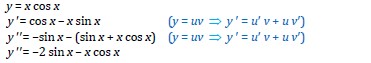
2. Turunan kedua dari y = (cos)2x adalah….
Penyelesaian:

Laju Yang Berkaitan

Hal utama dalam persoalan laju yang berkaitan adalah menghitung laju perubahan suatu besaran dalam bentuk laju perubahan besaran lain ( yang boleh jadi jauh lebih mudah diukur).
Jika variabel y tergantung kepada waktu, maka turunannya dy/dx disebut Laju Sesaat Perubahan.
Tentu saja, jika y mengukur jarak, maka laju sesaat perubahan ini juga disebut kecepatan (v). Laju sesaat dari perubahan kecepatan akan menghasilkan percepatan (a).
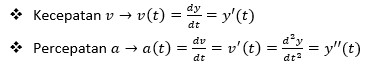
Banyak contoh dari laju sesaat dalam kehidupan sehari-hari, misalnya laju air mengalir ke dalam ember, laju membesarnya luas pencemaran minyak, laju bertambahnya nilai kapling tanah, dan lain-lain.
Strategi untuk pemecahan masalah khususnya mengenai laju yang berkaitan, adalah:
1. Baca masalah secara seksama.
2. Gambarkan diagram jika mungkin.
3. Perkenalkan notasi. Berikan lambing kepada semua besaran yang merupakan fungsi waktu.
4. Nyatakan informasi yang diketahui dan laju yang diperlukan dalam bentuk turunan.
5. Tuliskan persamaan yang mengaitkan beragam besaran dari masalah tersebut. Jika perlu, gunakan geometri untuk menghilangkan satu peubah melalui substitusi.
6. Gunakan aturan rantai untuk menurunkan kedua ruas persamaan terhadap t.
7. Substitusikan informasi yang diketahui ke dalam persamaan yang dihasilkan dan pecahkan untuk laju yang tidak diketahui tersebut.
Contoh:
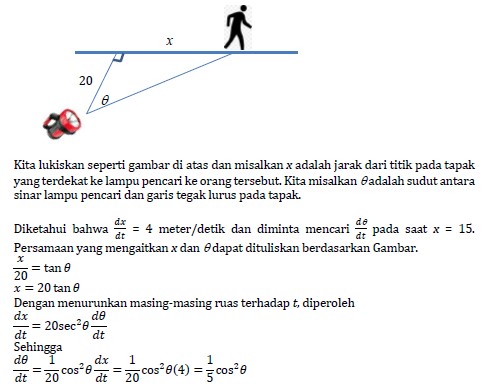
Seseorang berjalan menurut tapak lurus pada kecepatan 4 meter/detik. Lampu pencari terletak di tanah sejauh 20 meter dari tapak dan tetap dipusatkan pada orang itu. Pada laju berapa lampu pencari berputar jika orang itu berada 15 meter dari titik pada tapak yang terdekat ke lampu pencari?
Penyelesaian:

1.
Kerjakan soal berikut dengan tepat!
Turunan dari y = sin x + cos x adalah ....
A. 2 sin x
B. 2 cos x
C. sin x - cos x
D. cos x - sin x
E. 0
JAWABAN BENAR
D.
cos x - sin x
PEMBAHASAN
y = sin x + cos x
y = cos x – sin x
2.
Kerjakan soal berikut dengan tepat!
Jika f(x) = tan(3x2 + x – 1), nilai dari f’(x) sama dengan ....
A. (6x+1) sec2 (3x2 + x – 1)
B. (6x - 1) sec2 (3x2 + x – 1)
C. (6x) sec2 (3x2 + x – 1)
D. sec2 (3x2 + x – 1)
E. sec2 (6x+1)
JAWABAN BENAR
A.
(6x+1) sec2 (3x2 + x – 1)
PEMBAHASAN
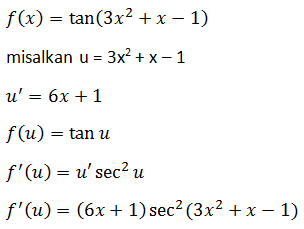
3.
Kerjakan soal berikut dengan tepat!
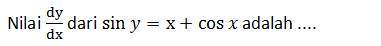
A.

B.

C.

D.

E.

JAWABAN BENAR
E.

PEMBAHASAN
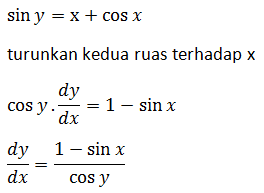
4.
Kerjakan soal berikut dengan tepat!
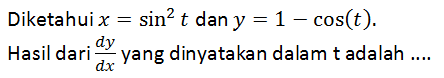
A.

B.

C.

D.

E.

JAWABAN BENAR
B.

PEMBAHASAN
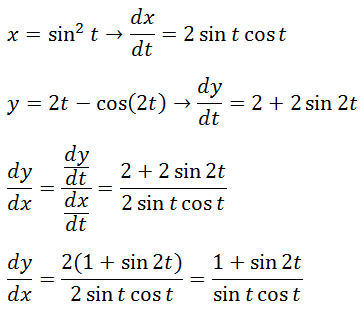
5.
Kerjakan soal berikut dengan tepat!
Turunan dari xy - cos xy = 1 adalah ....
A.

B.

C.

D.

E.

JAWABAN BENAR
E.

PEMBAHASAN
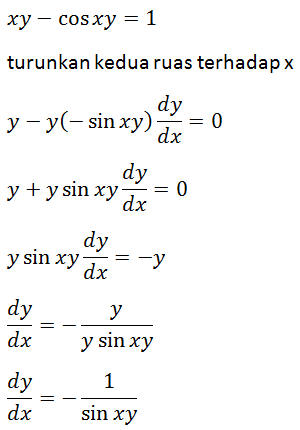
6.
Kerjakan soal berikut dengan tepat!
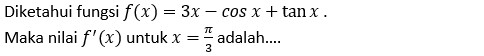
A.

B.

C.

D.

E.

JAWABAN BENAR
C.

PEMBAHASAN
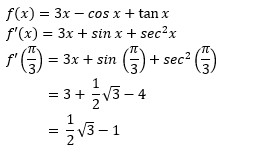
7.
Kerjakan soal berikut dengan tepat!
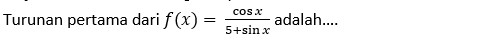
A.

B.

C.

D.

E.

JAWABAN BENAR
C.

PEMBAHASAN


Oops!!!
Yah, jawaban kamu meleset nih. Ingin melihat pembahasan soal ini?

BENAR!!!
Selamat!
Jawaban kamu benar. Ingin lihat pembahasan soal ini?
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved

