Belajar Pintar Materi SMP, SMA, SMK
BelajarPintarV3
Matematika Wajib
Statistika
MATERI
Penyajian Data dalam Bentuk Diagram

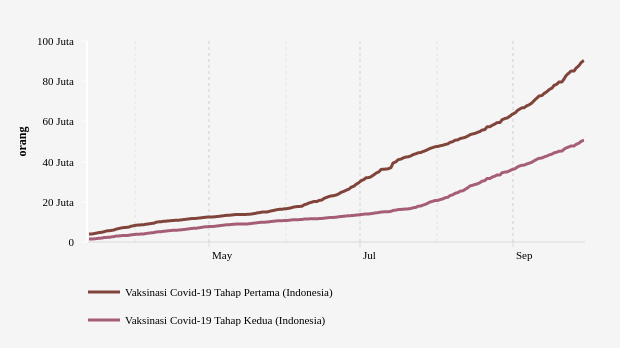
Sumber: databoks.katadata.co.id
Halo, Sobat Pintar! Apakah Sobat Pintar mengikuti perkembangan vaksinisasi yang sedang gencar diadakan oleh pemerintah?
Gambar diatas merupakan grafik perkembangan warga Indonesia yang sudah di vaksinisasi Covid-19 baik tahap 1 atau tahap 2 sampai dengan pertengahan bulan september 2021. Menurut sobat, berapa rata-rata warga Indonesia yang memperoleh vaksin tahap 1 setiap bulannya? Dan berapa rata-rata warga Indonesia yang memperoleh vaksin tahap 2 setiap bulannya? Kedua pertanyaan tersebut dapat kita jawab dengan memahami statistika lhoo, Sobat!
Yuk kita belajar bersama tentang statistika agar kita paham mengenai penyajian data.
Sobat Pintar sudah tau definisi Statistika belum?
Statistika ialah ilmu yang mempelajari tentang bagaimana merencanakan, menganalisis, menginterpretasi, mengumpulkan dan mempresentasikan data sehingga bisa dikatakan bahwa statistika merupakan ilmu yang berhubungan dengan data.
Terdapat banyak cara dalam menyajikan data dalam statistika, salah satunya penyajian data dalam bentuk diagram.
Berikut berbagai contoh diagram untuk menyajikan data dalam statistika
DIAGRAM GARIS
Penyajian data statistik dengan menggunakan diagram berbentuk garis lurus disebut diagram garis lurus atau diagram garis. Diagram garis biasanya digunakan untuk menyajikan data statistik yang diperoleh berdasarkan pengamatan dari waktu ke waktu secara berurutan.
Berikut contoh dari diagram garis:
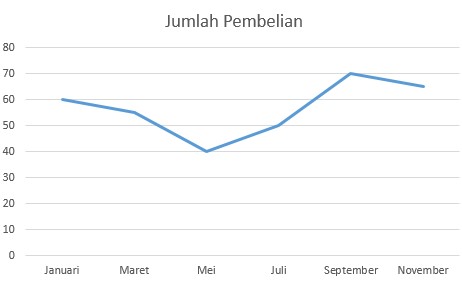
DIAGRAM BATANG
Diagram batang umumnya digunakan untuk menggambarkan perkembangan nilai suatu objek penelitian dalam kurun waktu tertentu. Diagram batang menunjukkan keterangan-keterangan dengan batang-batang tegak atau mendatar dan sama lebar dengan batang-batang terpisah.
Berikut contoh dari diagram batang:
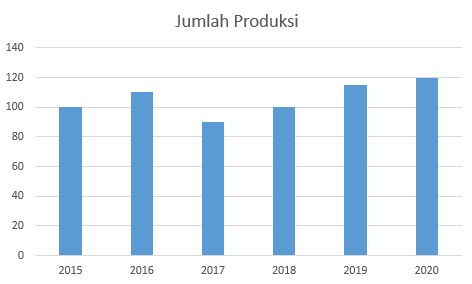
DIAGRAM LINGKARAN
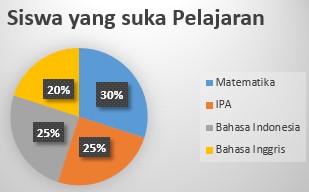
Diagram lingkaran adalah penyajian data statistik dengan menggunakan gambar yang berbentuk lingkaran. Bagian-bagian dari daerah lingkaran menunjukkan bagian-bagian atau persen dari keseluruhan. Untuk membuat diagram lingkaran, terlebih dahulu ditentukan besarnya persentase tiap objek terhadap keseluruhan data dan besarnya sudut pusat sektor lingkaran.
Berikut contoh dari diagram lingkaran:
Penyajian Data dengan Distribusi Frekuensi

Selain menyajikan data dengan diagram, terdapat cara penyajian data yang lain lho, Sobat Pintar. Apakah itu?
Yaa, tepat sekali, Penyajian Data dengan Distribusi Frekuensi. Yuk kita pelajari Penyajian Data dengan Distribusi Frekuensi!
DISTRIBUSI FREKUENSI TUNGGAL
Data tunggal seringkali dinyatakan dalam bentuk daftar bilangan, namun kadangkala dinyatakan dalam bentuk tabel distribusi frekuensi. Tabel Distribusi Frekuensi Tunggal merupakan cara untuk menyusun data yang relatif sedikit.
Berikut contoh dari penyajian data distribusi frekuensi tunggal:
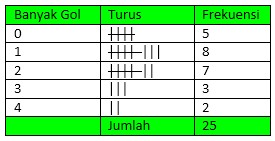
DISTRIBUSI FREKUENSI BERKELOMPOK
Data yang berukuran besar (n > 50) lebih tepat disajikan dalam Tabel Distribusi Frekuensi Kelompok, yaitu cara penyajian data yang datanya disusun dalam kelas-kelas tertentu.
Langkah-langkah penyusunan tabel distribusi frekuensi adalah sebagai berikut:
1. Menentukan Jangkauan (J) = Xmax - Xmin
2. Menentukan banyak interval (K) dengan rumus "Sturgess" yaitu: K= 1 + 3,3 log n dengan n adalah banyak data. Banyak kelas harus merupakan bilangan bulat positif hasil pembulatan ke bawah.
3. Menentukan panjang interval kelas (I) dengan menggunakan rumus : I=J/K
4. Menentukan batas-batas kelas. Data terkecil harus merupakan batas bawah interval kelas pertama atau data terbesar adalah batas atas interval kelas terakhir.
5. Memasukkan data ke dalam kelas-kelas yang sesuai dan menentukan nilai frekuensi setiap kelas.
Daftar distribusi kumulatif ada dua macam, yaitu:
• Daftar distribusi kumulatif kurang dari (menggunakan tepi atas).
• Daftar distribusi kumulatif lebih dari (menggunakan tepi bawah).
Berikut contoh dari penyajian data distribusi frekuensi kelompok :
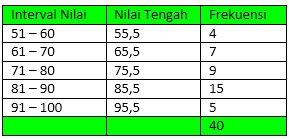
Histogram dan Poligon Frekuensi

Setelah kita mempelajari penyajian data dengan diagram dan distribusi frekuensi, selanjutnya kita akan membahas Penyajian Data dengan Histogram dan Poligon Frekuensi. Daripada penasaran, langsung simak materinya ya Sobat!!
HISTOGRAM
Dari suatu data yang diperoleh dapat disusun dalam tabel distribusi frekuensi dan disajikan dalam bentuk diagram yang disebut histogram. Jika pada diagram batang, gambar batang-batangnya terpisah maka pada histogram gambar batang-batangnya berimpit.
Berikut contoh dari histogram:
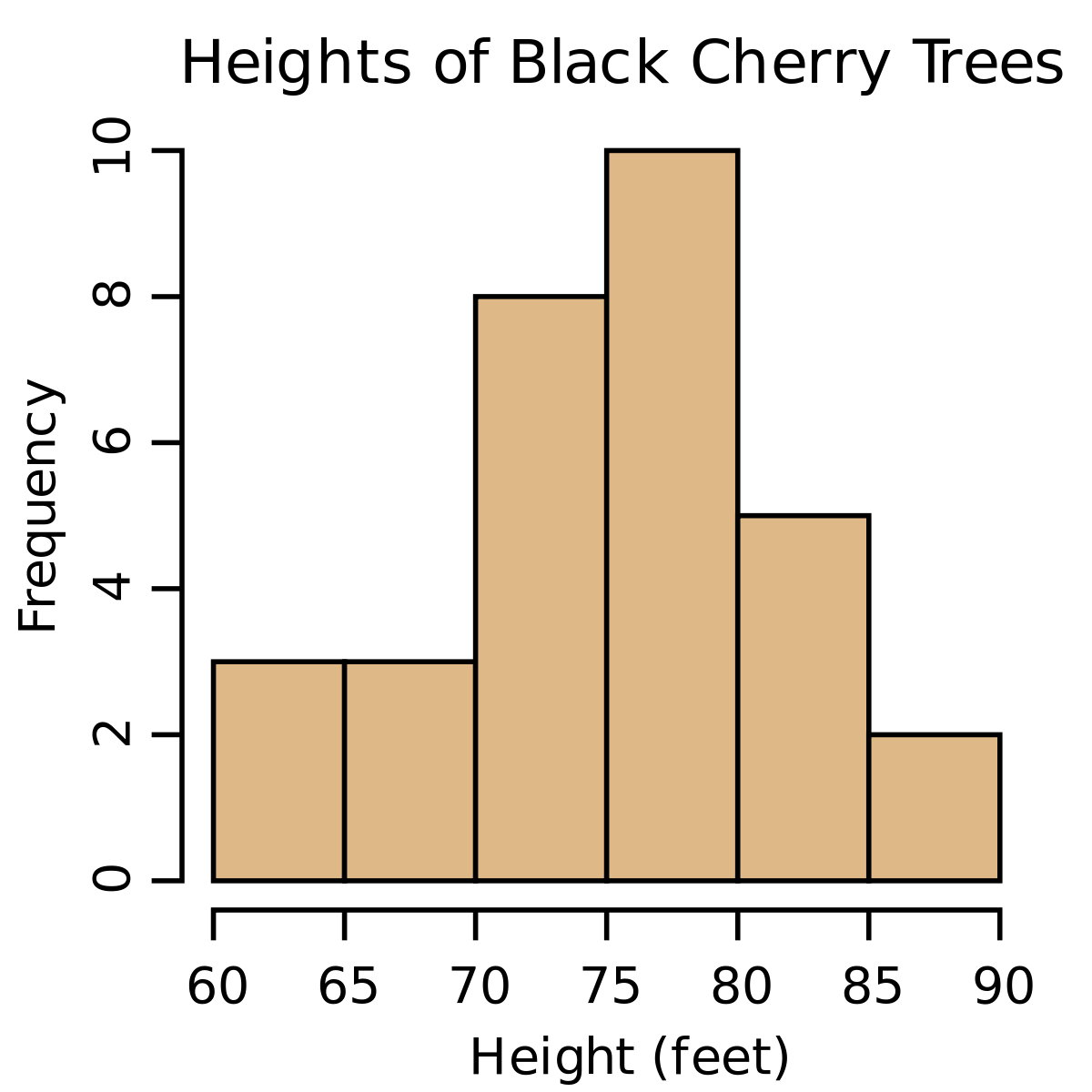
POLIGON FREKUENSI
Apabila pada titik-titik tengah dari histogram dihubungkan dengan garis dan batang-batangnya dihapus, maka akan diperoleh poligon frekuensi.
Berikut contoh dari poligon frekuensi:
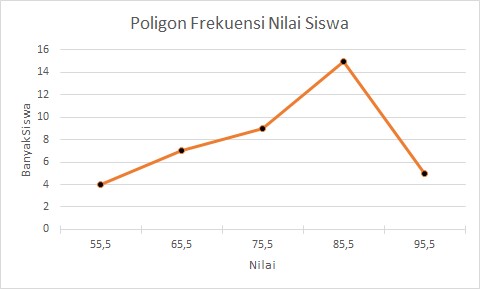
Ogive

Selanjutnya, kita akan membahas mengenai penyajian data dengan menggunakan Ogive. Apakah kalian pernah mendengar istilah ogive?
Ogive ternyata merupakan salah satu bentuk penyajian data dalam statistika loh! Yuk simak penjelasannya sebagai berikut!
Grafik yang menunjukkan frekuensi kumulatif kurang dari atau frekuensi kumulatif lebih dari disebut poligon kumulatif. Poligon kumulatif yang dibuat mulus hasilnya disebut ogive. Ada dua macam ogive, yaitu Ogive frekuensi kumulatif kurang dari disebut ogive positif dan Ogive frekuensi kumulatif lebih dari disebut ogive negatif.
Berikut contoh dari Ogive:
Diagram Pencar (Scatter Plot)
Diagram pencar termasuk salah satu bentuk penyajian data dalam statistika lho! Yuk simak penjelasannya sebagai berikut!
Scatter plot atau diagram pencar merupakan cara yang paling sederhana untuk menentukan hubungan antara sebab dan akibat dari dua variabel yang saling mempengaruhi atau tidak. Skala data yang digunakan harus menggunakan skala interval dan rasio.
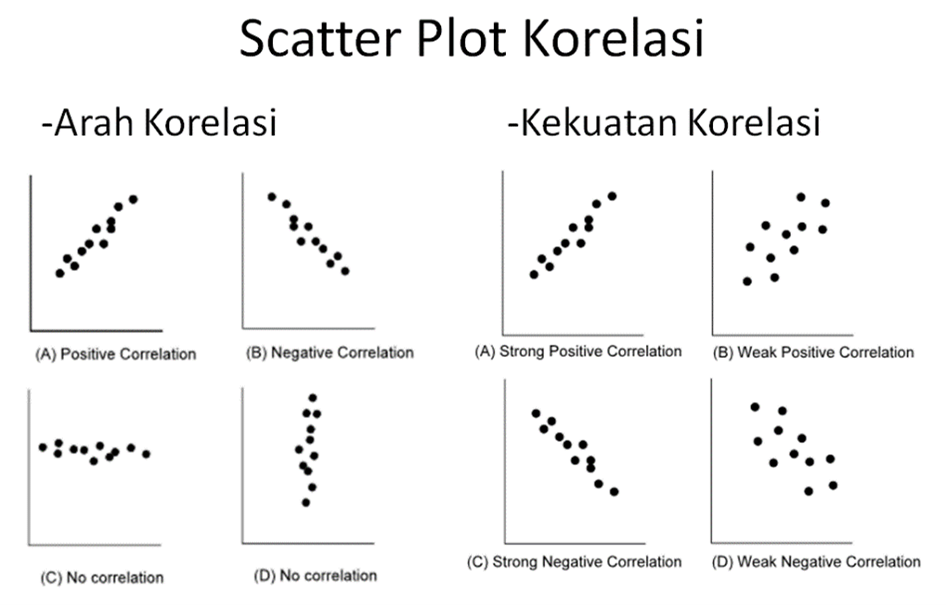
Hasil dari hubungan dua variabel pada diagram pencar memiliki beberapa makna ditinjau dari 2 segi, yaitu segi arah dan kekuatannya. Pola dari hubungan (korelasi) dua variabel berdasarkan arah korelasinya terbagi menjadi 3, yaitu korelasi positif, korelasi negatif, dan tidak ada korelasi. Sedangkan pola korelasi yang didasarkan pada kekuatan korelasinya terbagi menjadi 2, yaitu korelasi kuat dan korelasi lemah.
Berikut contoh diagram pencar berdasarkan pembagian pola korelasinya.
Contoh dari diagram pencar mengenai hubungan antara biaya iklan dengan penjualan produk :
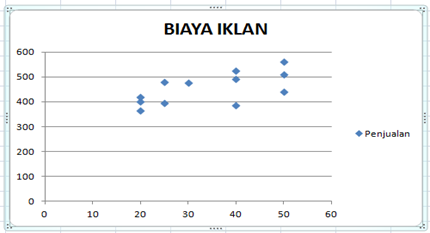
Diagram Titik (Dot Plot)
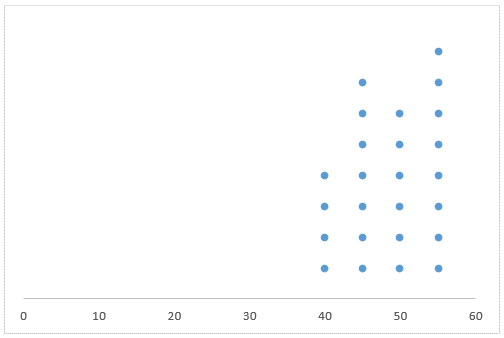
Diagram titik sebenarnya hampir sama dengan diagram batang. Namun dalam penyajiannya tidak berupa batang, melainkan titik-titik secara vertikal. Sumbu garis horizonal pada diagram titik menyatakan skala, sedangkan nilai pengamatan dinyatakan dalam titik di atas skala tersebut. Diagram titik dapat dimanfaatkan untuk mengetahui distribusi dari satu variabel. Contoh diagram titik :
Dalam sebuah kelas yang terdiri dari 20 anak, diperoleh data berat badan anak yang akan disajikan dalam diagram titik berikut
Box and Whisker Plot
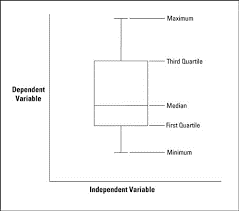
Box and Whisker Plot terdiri dari box yang berarti kotak dan whisker yang berarti kumis. Maksudnya adalah diagram ini dinyatakan dalam bentuk kotak persegi panjang dengan kanan dan kiri (maupun atas dan bawah) kotak tersebut terdapat garis yang menyerupai kumis. Diagram jenis ini digunakan untuk menampilkan distribusi nilai dari suatu data.
Data yang dapat dibaca dari box and whisker plot, yaitu nilai minimal, kuartil atas, median, kuartil bawah, serta nilai maksimal. Posisi dari ukuran penyebaran data tersebut bisa kalian perhatikan pada gambar berikut
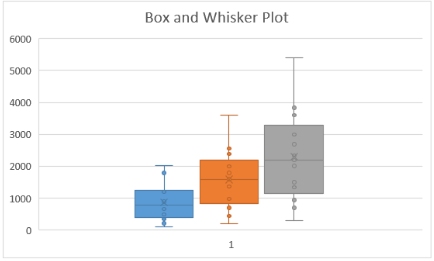
Contoh dari box and whisker plot:
1.
Perhatikan diagram lingkaran berikut!
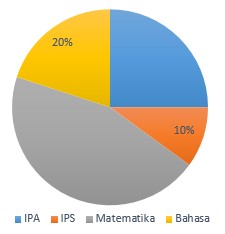
Jika diketahui jumlah siswa dari suatu kelas A ada sebanyak 200 siswa, jumlah siswa yang suka pelajaran matematika ada sebanyak ....
A. 45
B. 50
C. 90
D. 100
E. 110
JAWABAN BENAR
C.
90
PEMBAHASAN
Diketahui :
Siswa yang suka pelajaran IPS (IPS) = 10%
Siswa yang suka pelajaran Bahasa (Bahasa) = 20%
Siswa yang suka pelajaran IPA (IPA) = 25%
Jumlah Siswa kelas A (n) = 200
Menghitung berapa persen siswa yang suka pelajaran Matematika
100% = IPS% + Bahasa% + IPA% + Matematika%
100% = 10% + 20% + 25% + Matematika%
Matematika% = 100% – (10% + 20% + 25%)
Matematika% = 100% – 55%
Matematika% = 45%
Menghitung total siswa yang suka pelajaran Matematika
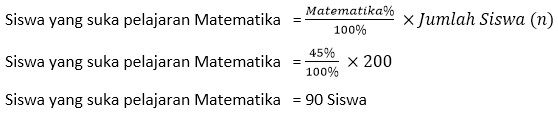
Jadi, total siswa yang suka pelajaran Matematika ada sebanyak 90 Siswa
2.
Perhatikan Diagram Garis berikut!
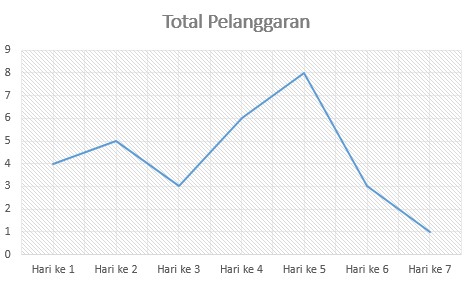
Bentuk tabel yang sesuai dengan diagram garis diatas adalah ....
A.

B.

C.

D.

E.

JAWABAN BENAR
E.

PEMBAHASAN
Dari gambar, bisa kita lihat jumlah pelanggar pada hari ke 1 ialah 4, pada hari ke 2 ialah 5, pada hari ke 3 ialah 3, pada hari ke 4 ialah 6, pada hari ke 5 ialah 8, pada hari ke 6 ialah 3, dan pada hari ke 7 ialah 1.
Jadi, jawaban yang sesuai pada tabel ialah E.

Oops!!!
Yah, jawaban kamu meleset nih. Ingin melihat pembahasan soal ini?

BENAR!!!
Selamat!
Jawaban kamu benar. Ingin lihat pembahasan soal ini?
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved

