Belajar Pintar Materi SMP, SMA, SMK
BelajarPintarV3
Matematika
Lingkaran
MATERI
Garis Singgung Persekutuan Luar Dua Lingkaran

Perhatikan gambar di bawah ini!
Lingkaran A berpusat di A dengan jari-jari AD = r1. Lingkaran B berpusat di B dengan jari-jari BE = r2.
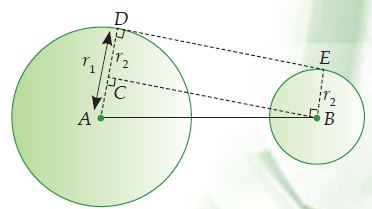
AB adalah jarak kedua titik pusat lingkaran (s). DE adalah garis singgung persekutuan luar dua lingkaran, dimana DE tegak lurus dengan AD. Melalui titik B, dapat ditarik garis BC yang sejajar garis DE (BC//DE), sehingga BE = CD = r2, dan sudut ACB = 90o.
Maka segitiga ACB adalah segitiga siku-siku, sehingga berlaku teorema Phythagoras,
AB2 = AC2 + BC2
BC2 = AB2 – AC2
= AB2 – (AD – CD)2
= s2 – (r1 – r2)2
Karena BC//DE dan sudut ACB = sudut ADE = 90o, maka DE = BC. Jadi, DE2 = s2 – (r1 – r2)2. Maka panjang garis singgung persekutuan luar dua lingkaran dirumuskan:
l2 = s2 – (r1 – r2)2
dengan r1 > r2, dan
l : panjang garis singgung persekutuan luar dua lingkaran
s : jarak antara kedua pusat dua lingkaran
r1: jari-jari lingkaran pertama
r2: jari-jari lingkaran kedua
Garis Singgung Persekutuan Dalam Dua Lingkaran

Perhatikan gambar di bawah ini!
Lingkaran A berpusat di A dengan jari-jari AC = r1. Lingkaran B berpusat di B dengan jari-jari BE = r2
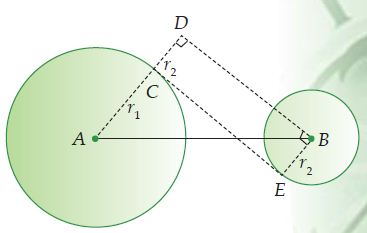
AB adalah jarak kedua titik pusat lingkaran (s). CE adalah garis singgung persekutuan dalam dua lingkaran, dimana CE tegak lurus dengan AC. Melalui titik B, kita dapat menarik garis BD yang sejajar dengan garis CE. (BD//CE), sehingga CD = BE = r2, dan sudut ADB = 90o.
Maka segitiga ADB adalah segitiga siku-siku, sehingga berlaku teorema Phythagoras, yaitu:
AB2 = AD2 + BD2
BD2 = AB2 – AD2
= AB2 – (AC + CD)2
= s2 – (r1 + r2)2
Karena BD//CE dan sudut ADB = sudut ACE = 90o, maka CE = BD. Jadi, CE2 = s2 – (r1 + r2)2. Sehingga, dapat kita simpulkan bahwa panjang garis singgung persekutuan dalam dua lingkaran adalah:
d2 = s2 – (r1 + r2)2
dengan r1 > r2, dan
d : panjang garis singgung persekutuan dalam dua lingkaran
s : jarak antara kedua pusat dua lingkaran
r1 : jari-jari lingkaran pertama
r2 : jari-jari lingkaran kedua
1.
Kerjakan soal dibawah ini dengan benar!
Diketahui dua buah lingkaran dengan pusat M dan N, dengan panjang jari-jari berturut-turut adalah 10 cm dan 25 cm. Jika jarak titik M dan N adalah 17 cm, maka panjang garis singgung persekutuan luar kedua lingkaran tersebut adalah …
A. 7
B. 8
C. 49
D. 64
JAWABAN BENAR
B.
8
PEMBAHASAN
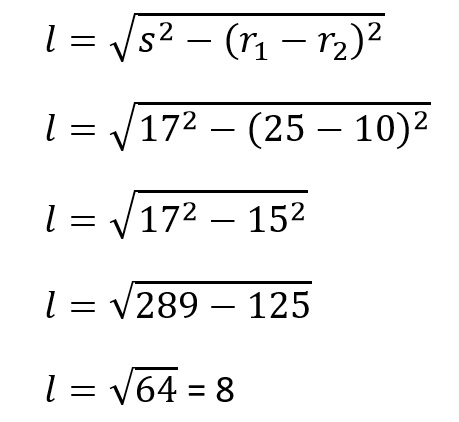
2.
Kerjakan soal dibawah ini dengan benar!
Panjang garis singgung persekutuan dalam dua lingkaran adalah 15 cm. Panjang jari-jari lingkaran yang besar adalah 6 cm. Jika jarak antara kedua titik pusat sama dengan 17 cm, berapa panjang jari-jari yang lingkaran kecil?
A. 2
B. 4
C. 6
D. 8
JAWABAN BENAR
A.
2
PEMBAHASAN
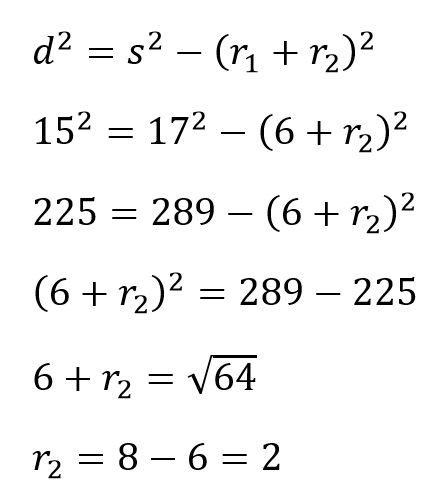
3.
Kerjakan soal dibawah ini dengan benar!
Diketahui dua buah lingkaran dengan pusat M dan N, dengan panjang jari-jari berturut-turut adalah 15 cm dan 27 cm. Jika jarak titik M dan N adalah 13 cm, maka panjang garis singgung persekutuan luar kedua lingkaran tersebut adalah …
A. 5
B. 8
C. 49
D. 64
JAWABAN BENAR
A.
5
PEMBAHASAN
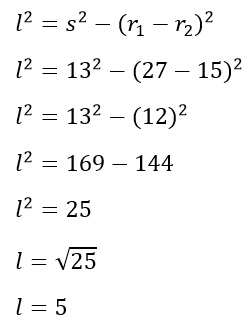
4.
Kerjakan soal dibawah ini dengan benar!
Panjang garis singgung persekutuan dalam dua lingkaran adalah 12 cm. Panjang jari-jari lingkaran yang besar adalah 3cm. Jika jarak antara kedua titik pusat sama dengan 13 cm, berapa panjang jari-jari yang lingkaran kecil?
A. 2
B. 4
C. 6
D. 8
JAWABAN BENAR
A.
2
PEMBAHASAN
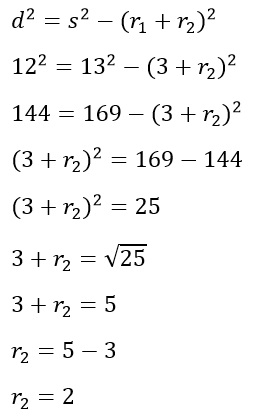

Oops!!!
Yah, jawaban kamu meleset nih. Ingin melihat pembahasan soal ini?

BENAR!!!
Selamat!
Jawaban kamu benar. Ingin lihat pembahasan soal ini?
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved

