Materi Matematika Minat - Turunan Fungsi Trigonometri Kelas 12 MIA - Belajar Pintar
BelajarPintarV3
Peta Belajar Bersama
Hai, Sobat!
Sebelum kamu belajar tentang Turunan Fungsi Trigonometri, coba kalian perhatikan Peta Belajar Bersama ini dulu, ya!
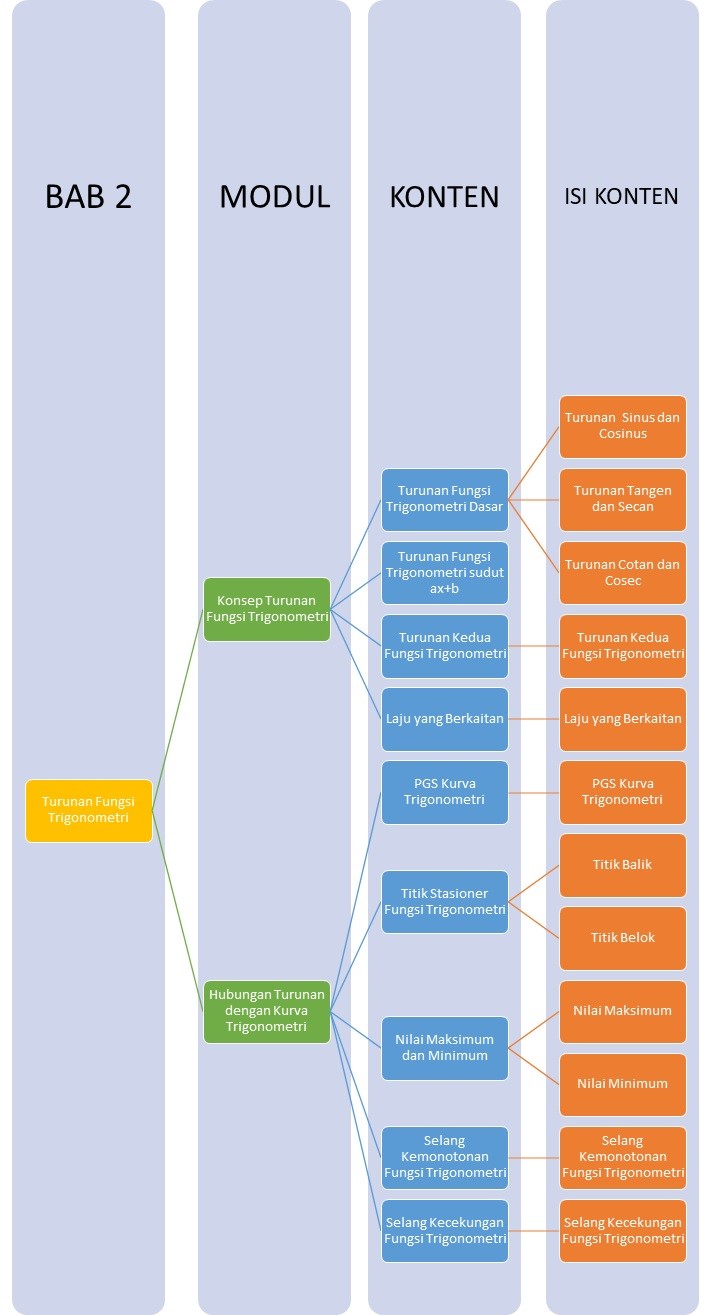
Yuk, kita mulai belajar Bersama!
Turunan Fungsi Trigonometri Dasar

Masih ingat dengan materi turunan fungsi yang pernah kalian pelajari saat kelas 11 kemarin?
Nah, masih dalam pokok bahasan turunan, kali ini kita akan belajar mengenai turunan pada fungsi trigonometri. Jadi, fungsinya mencakup perbandingan trigonometri seperti : sinus, cosinus, tangen, cosecan, secan, dan cotangen.
Buat sobat pintar yang lupa apa itu turunan, akan sedikit dijelaskan konsep umum dari turunan suatu fungsi.
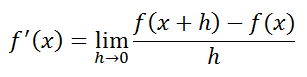
Definisi tersebut dapat digunakan dalam fungsi trigonometri, baik itu fungsi sinus, cosinus, tangen, cosecan, secan, dan cotangen yang akan dijabarkan sebagai berikut.
TURUNAN FUNGSI SINUS
Turunan fungsi sinus dapat ditentukan dengan cara berikut:
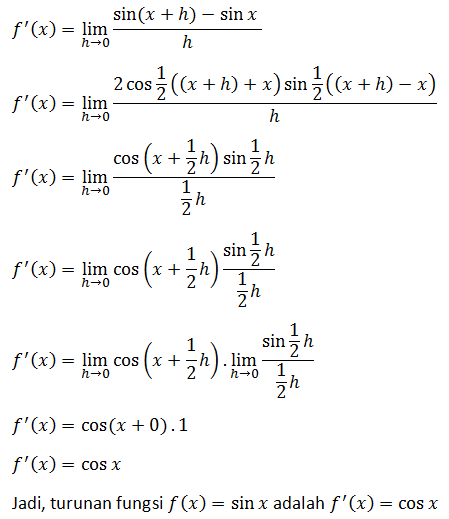
TURUNAN FUNGSI COSINUS
Turunan fungsi cosinus dapat ditentukan dengan cara berikut:
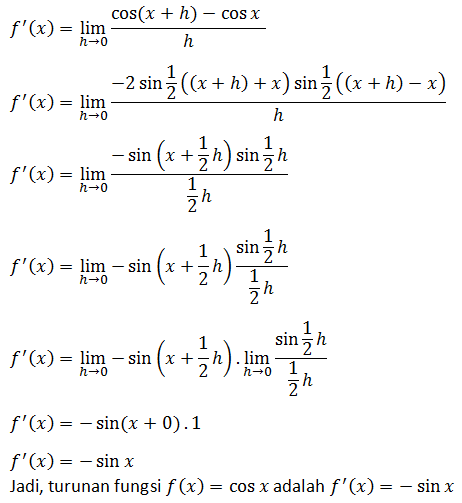
TURUNAN FUNGSI TANGEN

TURUNAN FUNGSI COSECAN
Turunan fungsi cosec dapat ditentukan dengan cara berikut;

TURUNAN FUNGSI SECAN
Turunan fungsi secan dapat ditentukan dengan cara berikut;

TURUNAN FUNGSI COTANGEN
Turunan fungsi cotan dapat ditentukan dengan cara berikut;


Berdasarkan penjabaran di atas, turunan dasar dari fungsi trigonometri, yaitu:

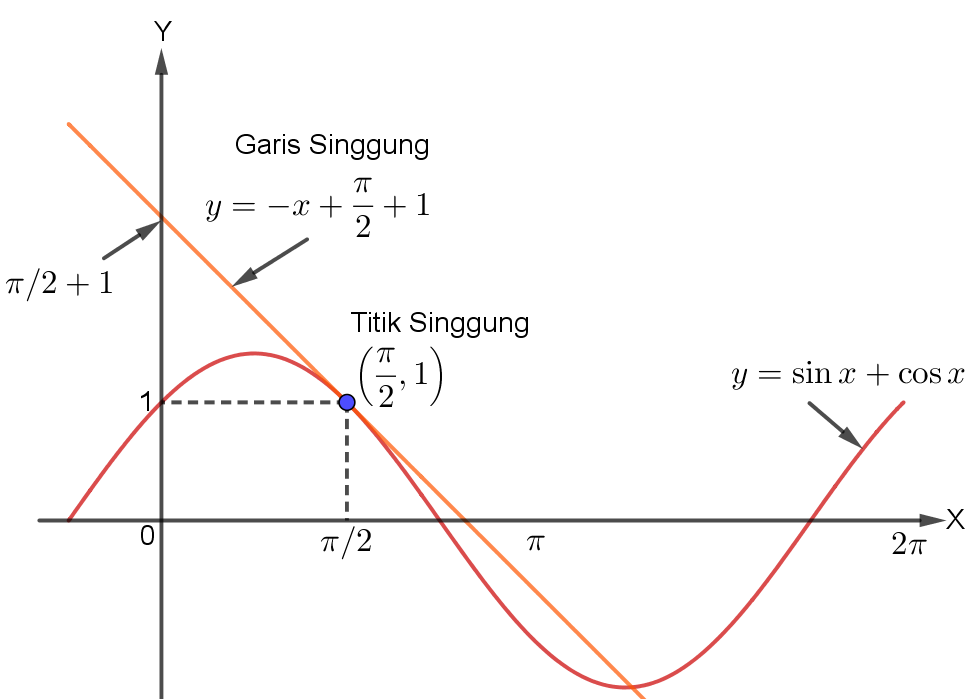
Persamaan Garis Singgung Suatu Kurva

Sumber : mathcyber1997.com
Hubungan turunan dengan kurva fungsi trigonometri hampir sama dengan aplikasi turunan dalam fungsi aljabar lho, Sobat!
Kalian sudah tahu kurva dari fungsi trigonometri, kan?
Nah, berdasarkan kurva-kurva trigonometri, kita bisa mencari tahu persamaan garis singgung, nilai maksimum dan minimum, titik belok, selang kemonotonan, serta selang kecekungan.
Langsung kita bahas aja yuk!
PERSAMAAN GARIS SINGGUNG KURVA
Sobat Pintar masih ingat cara mencari persamaan garis singgung dari sebuah kurva?
Yap! Kita membutuhkan gradien serta sebuah titik singgung pada kurva tersebut untuk mencari persamaan garis singgungnya.
Nah, dalam menentukan gradien dari persamaan garis singgung, kita bisa memanfaatkan aplikasi turunan, Sobat.
Masih ingat tidak ya?
Jadi, gradien garis singgung kurva y = f(x) di titik (x1, y1) adalah m = f’(x1).
Sehingga persamaan garis singgungnyaa adalah y – y1 = m (x – x1).
Pada fungsi trigonometri, konsep untuk mencari gradien dari kurva trigonometri juga sama, yaitu dengan memanfaatkan aplikasi turunan fungsi trigonometri.
Materi Matematika Minat SMA - 12 MIA Lainnya
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved








