Materi Matematika Minat - Distribusi Peluang Kelas 12 MIA - Belajar Pintar
BelajarPintarV3
Peta Belajar Bersama
Halo, Sobat Pintar!
Sebelum kita mempelajari tentang DISTRIBUSI PELUANG, coba perhatikan Peta Belajar Bersama berikut ya!
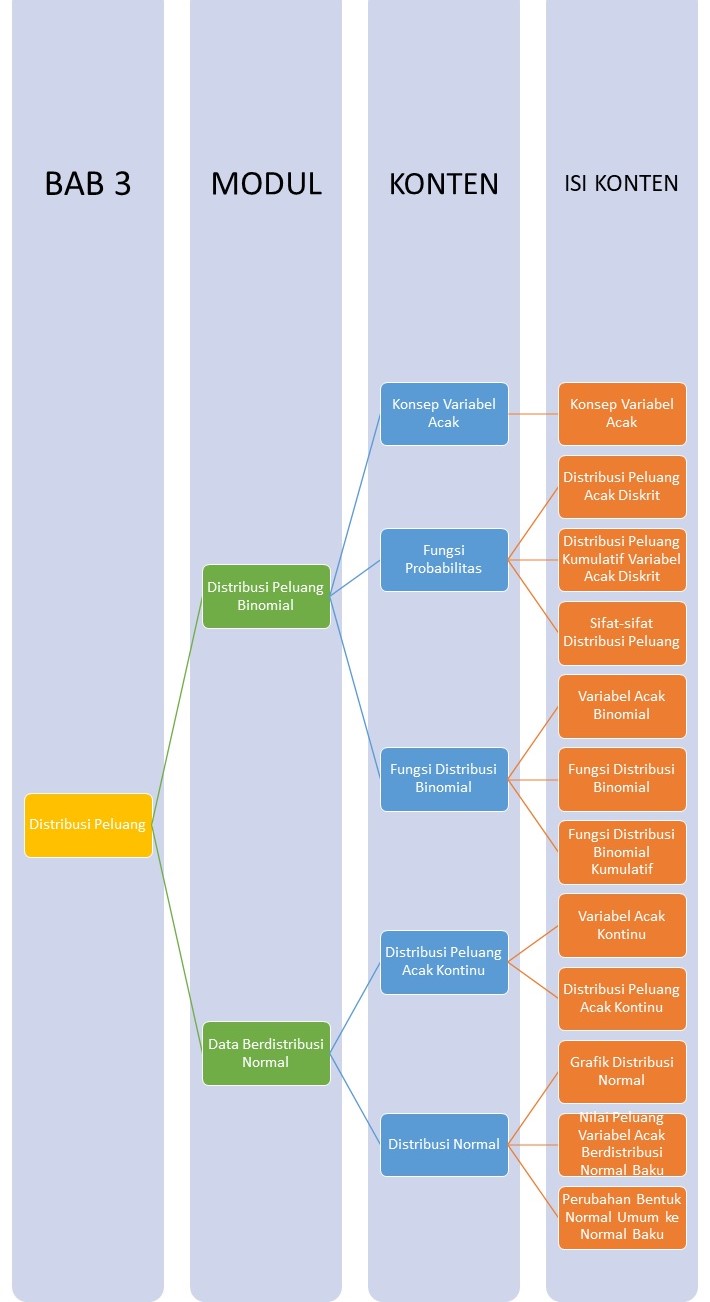
Yuk, kita mulai belajar Bersama!
Konsep Variabel Acak

Halo Sobat Pintar! Ada yang tau sebelumnya apa itu variabel?
Nah variabel merupakan suatu besaran yang memiliki nilai tidak tunggal, misalnya bilangan asli kurang dari 10, bilangan bulat kurang dari 3, dan waktu tempuh kendaraan.
Jenis variabel ada dua yaitu variabel diskrit dan variabel kontinu.
Variabel diskrit memiliki nilai-nilai yang dapat dihitung, sedangkan variabel kontinu memiliki nilai-nilai yang tidak dapat dihitung.
Variabel acak merupakan variabel yang nilainya ditentukan oleh hasil percobaan, Variabel acak pun sama ada variabel acak diskrit dan ada variabel acak kontinu.
- Variabel acak diskrit diperoleh dari hasil menghitung/membilang, nilainya berupa bilangan bulat.
- Variabel acak kontinu diperoleh dari hasil mengukur dan nilainya berupa bilangan riil.
Contoh soal:
1. Widi melakukan pelemparan sebuah dadu satu kali. Hasil yang mungkin diperoleh Widi adalah....
Pembahasan:
Misalkan X = mata dadu yang muncul sehingga dapat anda nyatakan bahwa X = {1,2,3,4,5,6}.
2. Irwan melemparkan satu keping uang logam sebanyak dua kali. Irwan mengamati banyak hasil angka yang diperoleh adalah….
Pembahasan:
Misalkan X = banyak hasil angka yang diperoleh sehingga X = {0, 1,2}
Distribusi Peluang Acak Kontinu

Variabel Acak Kontinu
Sobat pintar sebelumnya sudah tau kan soal variabel acak diskrit?
Berbeda dengan variabel acak diskrit variabel acak kontinu menggunakan bilangan riil untuk menyatakan hasil suatu percobaan.
Variabel acak kontinu diperoleh dari hasil mengukur dan nilainya berupa bilangan riil.
Nilai-nilai variabel acak kontinu jika digambarkan pada garis interval berupa deretan titik-titik yang saling tersambung membentuk garis.
Sebagai contoh hasil pengukuran tinggi badan, hasil pengukuran suhu tubuh, dan lain-lain.
Contoh:
Pada suatu kelas yang beranggotakan 35 siswa dilakukan pengukuran tinggi badan siswa. Dari data hasil pengukuran tinggi badan tersebut diperoleh tinggi badan siswa tertinggi yaitu 175 cm dan terpendek 150 cm. Tentukan variabel acak yang menyatakan hasil pengukuran tinggi badan tersebut!
Pembahasan:
Tinggi badan siswa tertinggi adalah 175 cm dan terpendek adalah 150 cm.
Jika tinggi badan siswa dinyatakan dalam t maka nilainya adalah 150 < t < 175.
Variabel acak t menyatakan tinggi badan siswa. maka T = {t| 150 < t < 175 }.
Distribusi Peluang Variabel Acak Kontinu
Variabel acak kontinu berupa interval bilangan pada garis bilangan riil.

Keempat syarat tersebut harus terpenuhi ya! Jika salah satu dari empat syarat tersebut tidak terpenuhi maka fungsi peluang variabel acak kontinu bukan merupakan fungsi f(x).
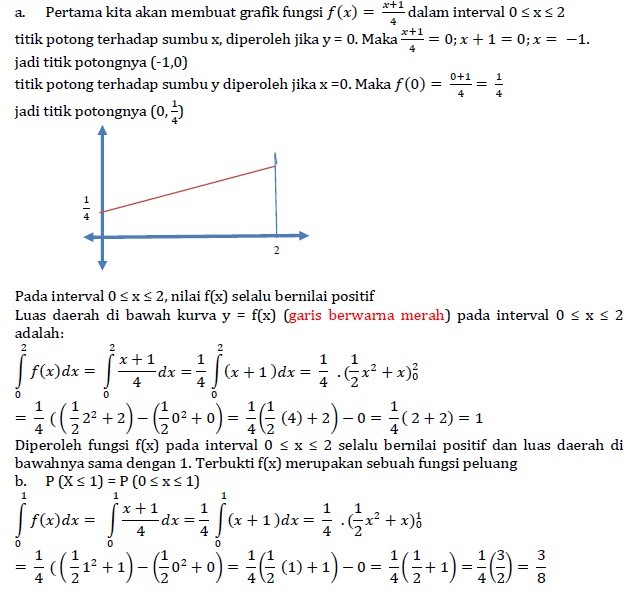
Contoh:

Pembahasan:
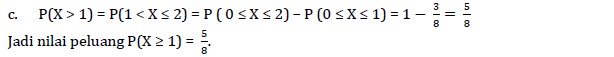
Materi Matematika Minat SMA - 12 MIA Lainnya
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved








