Materi Matematika IPA - Fungsi Komposisi dan Fungsi Invers Kelas Persiapan SBMPTN - Belajar Pintar
BelajarPintarV3
Pengertian Fungsi
Amati gambar berikut !
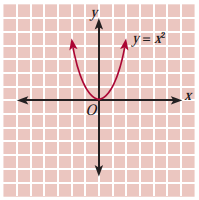
Pada gambar tersebut, relasi {(x, y)|y = x2; x, y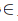 R}, setiap unsur pada daerah asal dihubungkan dengan satu dan hanya satu unsur pada daerah hasil; –2 dihubungan dengan 4, –1 dengan 1, 0 dengan 0, 1 dengan 1, 2 dengan 4, dan seterusnya. Relasi {(x, y)|y = 2x; x, y
R}, setiap unsur pada daerah asal dihubungkan dengan satu dan hanya satu unsur pada daerah hasil; –2 dihubungan dengan 4, –1 dengan 1, 0 dengan 0, 1 dengan 1, 2 dengan 4, dan seterusnya. Relasi {(x, y)|y = 2x; x, y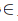 R} dan relasi {(x, y)|y = x2; x, y
R} dan relasi {(x, y)|y = x2; x, y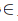 R} disebut fungsi.
R} disebut fungsi.
Kesimpulan :
Fungsi ialah relasi dengan setiap unsur dari daerah asalnya dipasangkan dengan tepat satu unsur dari daerah kawannya.
Contoh
Diketahui fungsi f : R—R dan f(x) = x2 – 1. Hitunglah f(–3), f(–1), f(0), f(2), dan f(3).
Jawab :
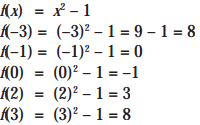
Penjumlahan Fungsi
Jika ada dua buah fungsi f dan g maka berlaku :
(f + g)(x) = f(x) + g(x)
Contoh :
f(x) = x + 2
g(x) = x2 - 4
Tentukan (f + g)(x) = ....
(f + g)(x) = f(x) + g(x)
(f + g)(x) = x + 2 + x2 - 4
(f + g)(x) = x2 + x - 2
Pengertian Fungsi Invers
1. f-1(x) adalah invers dari fungsi f(x)
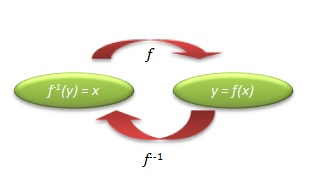
2. Menentukan fungsi invers : mengganti "f(x) = y = ... " menjadi "f-1(y) = x = ... "
3. Hubungan sifat fungsi invers dengan fungsi komposisi :
a. (f o f-1)(x) = (f-1 o f)(x) = I(x)
b. (f o g)-1(x) = (g-1 o f-1)(x)
3. (f o g)(x) = h(x) maka f(x) = (h o g-1)(x)

Materi Matematika IPA SMA - Persiapan SBMPTN Lainnya

Persamaan Kuadrat
0 Sub Bab Materi

Fungsi Kuadrat
0 Sub Bab Materi

Pertidaksamaan
0 Sub Bab Materi

Program Linier
0 Sub Bab Materi

Relasi dan Fungsi
0 Sub Bab Materi

Statistika
1 Sub Bab Materi

Limit dan Deferensial
0 Sub Bab Materi

Eksponen dan Logaritma
0 Sub Bab Materi

Barisan dan Deret
0 Sub Bab Materi

Sistem Persamaan Linier
0 Sub Bab Materi

Permutasi dan Kombinasi
0 Sub Bab Materi

Logika
0 Sub Bab Materi

Antar Ruang Lingkup
0 Sub Bab Materi

Bangun Ruang
0 Sub Bab Materi

Permutasi dan Kombinasi
2 Sub Bab Materi
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved







