Belajar Pintar Materi SMP, SMA, SMK
BelajarPintarV3
Matematika
Barisan, Deret dan Notasi Sigma
MATERI
Barisan Geometri
berbeda dengan deret geometri, kali ini kita akan bahas tentang barisan geometri. Barisan Geometri Merupakan suatu barisan bilangan yang setiap sukunya diperoleh dengan cara mengalikan suku di depannya dengan bilangan yang tetap (konstan).
U1, U2, U3, U4, ……. Un
jika ditulis bahasa matematikanya adalah sebagai berikut
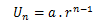
Dengan keterangan sebagai berikut :
Un = Suku ke- n
a = U1 = Suku Pertama
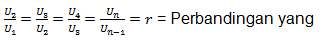 berdekatan = ratio
berdekatan = ratio
n = bilangan suku
Jika sobat pintar masih kurang paham, yuk sobat pintar simak soal latihan berikut
Diketahui barisan geometri: 2, 4, 6, 8, 10, …..
Tentukanlah suku ke 7
Penyelesaian :
a = 2, r = 2 dan n = 7
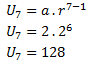
bagaimana sobat pintar? mudah dipahami bukan?
Deret Geometri
Sub bab selanjutnya, yuk kita pelajari deret geometri. Deret geometri terbagi menjadi 2 yaitu deret divergen dan deret konvergen.
Deret Divergen merupakan Deret yang tidak memiliki limit jumlah, kemudian Deret Konvergen merupakan Deret yang memiliki limit jumlah.
jika ditulis dalam kalimat matematika adalah sebagai berikut :
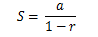
Dengan :
S = Limit jumlah deret
a = suku pertama
r = rasio
Deret Geometri Tak Terhingga
Deret geometri tak hingga adalah deret geometri dengan |r| < 1. Jumlah S dari dert geometri tak hingga adalah
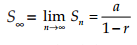
Rumus pada deret geometri berlaku juga untuk n tak terhingga. Adapun untuk n tak terhingga terdapat dua kasus yang harus kalian perhatikan, yaitu:
Kasus 1
Jika 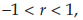 maka
maka 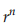 menuju 0.
menuju 0.
Sehingga, 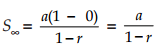
Deret geometri dengan 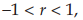 ini disebut deret geometri konvergen (memusat).
ini disebut deret geometri konvergen (memusat).
Kasus 2
Jika r< -1 atau r>1, maka untuk 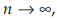 nilai
nilai 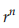 makin besar.
makin besar.
untuk r< -1, 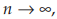 dengan n ganjil didapat
dengan n ganjil didapat 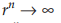
untuk r<-1, 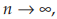 dengan n genap didapat
dengan n genap didapat 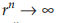
untuk r> 1, 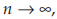 didapat
didapat 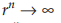
Akibatnya , 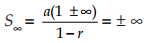
Deret geometri dengan r <-1 atau r > 1 ini disebut deret geometri divergen
(memencar).
1. Jumlah deret geometri tak hingga 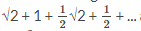 adalah
adalah
A. 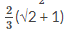
B. 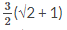
C. 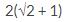
D. 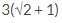
E. 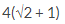
JAWABAN BENAR
C.
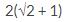
PEMBAHASAN
Jumlah deret geometri tak hingga dengan  maka
maka
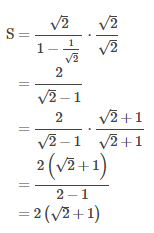
2. Barisan geometri dengan suku ke-5 adalah 1/3 dan rasio = 1/3, maka suku ke-9 barisan geometri tersebut adalah
A. 27
B. 9
C. 1/27
D. 1/81
E. 1/243
JAWABAN BENAR
E.
1/243
PEMBAHASAN
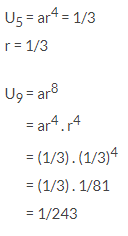

Oops!!!
Yah, jawaban kamu meleset nih. Ingin melihat pembahasan soal ini?

BENAR!!!
Selamat!
Jawaban kamu benar. Ingin lihat pembahasan soal ini?
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved

