Belajar Pintar Materi SMP, SMA, SMK
BelajarPintarV3
Matematika Wajib
Pertidaksamaan Rasional dan Irasional
MATERI
Konsep Pertidaksamaan Rasional Satu Variabel

Setelah membahas mengenai pertidaksamaan nilai mutlak, pernahkah kalian menemukan soal pertidaksamaan dengan bentuk pecahan atau bahkan bentuk akar?
Wah, kelihatannya sulit ya untuk diselesaikan. Eitss.. ternyata mudah kok menyelesaikannya jika kalian tahu triknya!
Yuk kita pelajari bersama mengenai pertidaksamaan rasional dan pertidaksamaan irasional.
Pertidaksamaan rasional adalah bentuk pertidaksamaan yang memuat fungsi rasional, yaitu fungsi yang dapat dinyatakan dalam bentuk

Bentuk umum dari pertidaksamaan rasional dapat dituliskan:
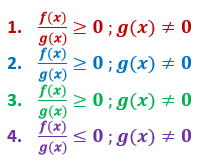
Note: Next untuk memahami contoh soal dari bentuk pertidaksamaan rasional di atas, ya, Sobat!
Langkah-langkah untuk menentukan himpunan penyelesaian pertidaksamaan rasional yaitu:
- Nyatakan fungsi dalam bentuk umum
- Tentukan pembuat nol pada pembilang dan penyebut, misal f(x)=0 dan g(x)=0
- Perhatikan syarat bahwa penyebut tidak boleh sama dengan nol
- Buat garis bilangan, kemudian tuliskan pembuat nol sesuai urutan pada garis bilangan
- Tentukan tanda pada untuk tiap interval pada garis bilangan
- Tentukan daerah penyelesaiannya dengan ketentuan :
- pertidaksamaan > atau >, daerah penyelesaiannya berada pada interval bertanda positif
- pertidaksamaan < atau <, daerah penyelesaiannya berada pada interval bertanda negatif
7. Himpunan penyelesaiannya adalah interval yang memuat daerah penyelesaian
LARANGAN!!!
Hal-hal yang tidak dibenarkan dalam menyelesaikan pertidaksamaan rasional, yaitu:
- Kali silang,
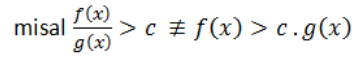
- Mencoret fungsi ataupun faktor yang sama pada pembilang dan penyebut
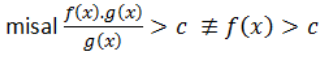
Contoh Pertidaksamaan Rasional Satu Variabel

Berikut merupakan contoh dan pembahasan soal pertidaksamaan rasional satu variabel:

Pembahasan:
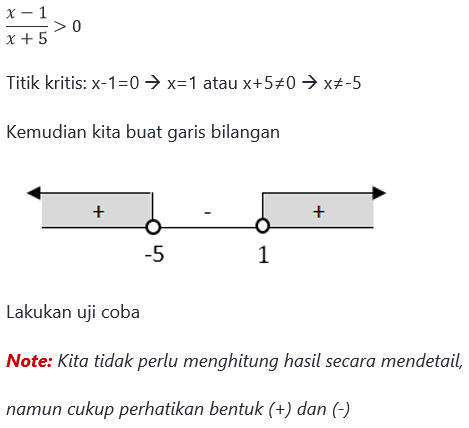
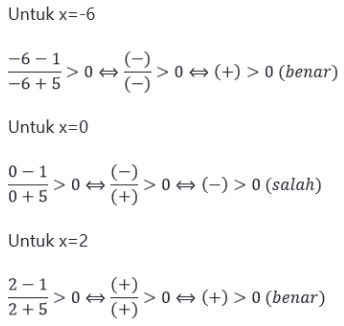
Lalu kita perhatikan tanda pertidaksamaan yaitu lebih dari sehingga arsir daerah penyelesaian bertanda positif.
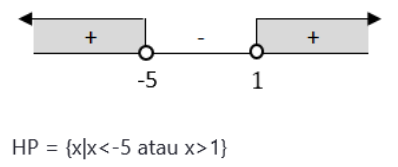

Pembahasan:


Lalu kita perhatikan tanda pertidaksamaan yaitu kurang dari sehingga arsir daerah penyelesaian bertanda negatif.
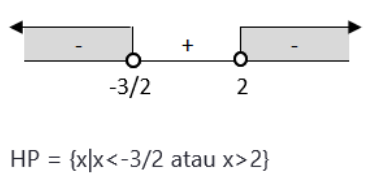
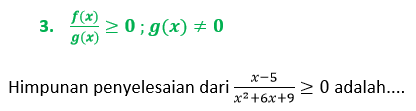
Pembahasan:

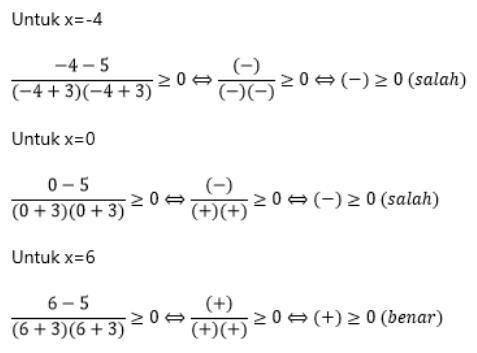
Lalu kita perhatikan tanda pertidaksamaan yaitu lebih dari sehingga arsir daerah penyelesaian bertanda positif.
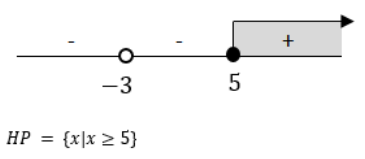

Pembahasan:


1.
Jawablah soal berikut ini!
![]()
A. x < 5/2
B. x > -3
C. -3 < x < 5/2
D. x < -3 atau x > 5/2
E. x < -3
JAWABAN BENAR
D.
x < -3 atau x > 5/2
PEMBAHASAN
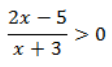
2x-5=0 x+3=0
2x=5 x=-3
x=5/2
Syarat :
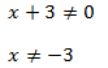
Menguji simbol + / – jika x<-3 dengan x= – 4 pada pertidaksamaan awal
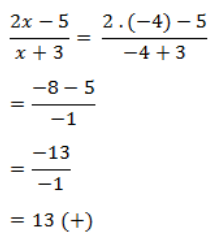
Menguji simbol + / – jika -3<x<5/2 dengan x= –0 pada pertidaksamaan awal
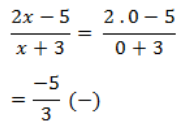
Menguji simbol + / – jika x>5/2 dengan x= 5 pada pertidaksamaan awal
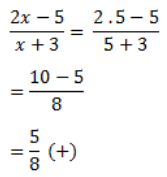
Diperoleh garis bilangan sebagai berikut:

Karena pada soal diminta simbol “>” jadi HP={x<-3 atau x>5/2}
2.
Jawablah soal berikut ini!

A.

B.

C.

D.

E.

JAWABAN BENAR
D.

PEMBAHASAN
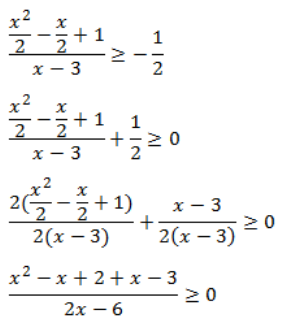
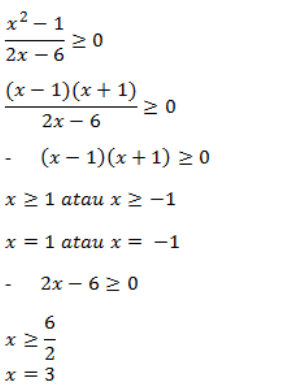
Syarat :
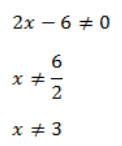
Menguji simbol + / – jika x < -1 dengan x= – 2 pada pertidaksamaan awal
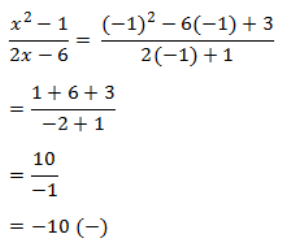
Menguji simbol + / – jika -1 < x < 1 dengan x = 0 pada pertidaksamaan awal
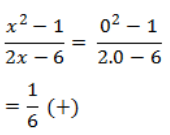
Menguji simbol + / – jika 1 < x < 3 dengan x = 2 pada pertidaksamaan awal
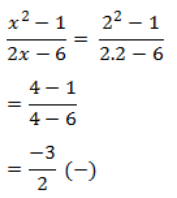
Menguji simbol + / – jika x > 3 dengan x = 4 pada pertidaksamaan awal
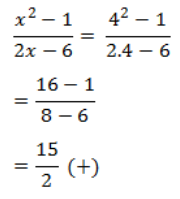
Diperoleh garis bilangan sebagai berikut:
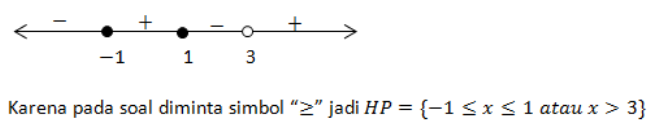
3.
Jawablah soal berikut ini!
![]()
A.

B.

C.

D.

E.

JAWABAN BENAR
B.

PEMBAHASAN
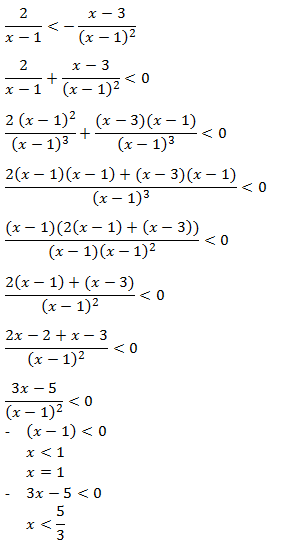
Syarat :
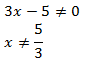
Menguji simbol + / – jika x < 1 dengan x = 0 pada pertidaksamaan
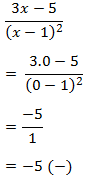
Menguji simbol + / – jika 1 < x < 5/3 dengan x = 1/2 pada pertidaksamaan awal
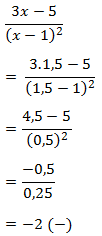
Menguji simbol + / – jika x > 5/3 dengan x = 2 pada pertidaksamaan awal
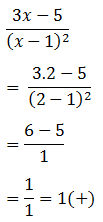
Diperoleh garis bilangan sebagai berikut:
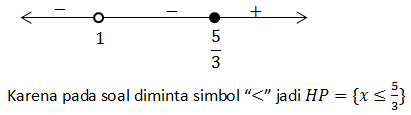
4.
Jawablah soal berikut ini!
![]()
A.

B.

C.

D.

E.

JAWABAN BENAR
B.

PEMBAHASAN


Lalu kita perhatikan tanda pertidaksamaan yaitu lebih dari sehingga arsir daerah penyelesaian bertanda positif.
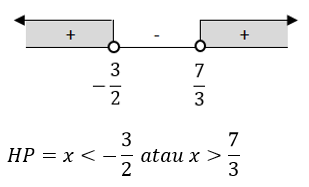
5.
Jawablah soal berikut ini!
![]()
A.

B.

C.

D.

E.

JAWABAN BENAR
A.

PEMBAHASAN


Oops!!!
Yah, jawaban kamu meleset nih. Ingin melihat pembahasan soal ini?

BENAR!!!
Selamat!
Jawaban kamu benar. Ingin lihat pembahasan soal ini?
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved

