Daftar Materi
MATERI
Luas Segitiga Tanpa Perbandingan Trigonometri
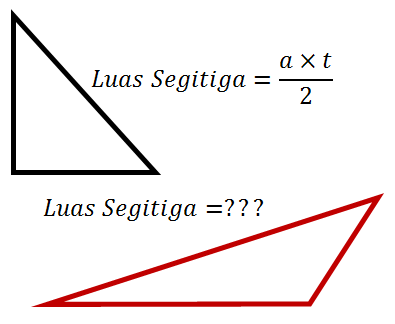
Setelah melihat gambar segitiga di atas, menurut kalian bagaimana cara kita mencari luasnya?
Dalam mencari luas segitiga, rumus apa yang kalian gunakan, Sobat?
Sobat Pintar tahu tidak bahwa dalam mencari luas segitiga, terdapat beberapa rumus lain selain rumus setengah kali luas alas kali tinggi lho!
Kira-kira apa saja ya rumusnya?
Simak baik-baik penjelasan berikut yuk!
RUMUS LUAS SEGITIGA JIKA DIKETAHUI PANJANG ALAS DAN TINGGINYA
Rumus luas segitiga ini pasti sudah diketahui oleh Sobat Pintar semuanya. Rumus ini digunakan jika sebuah segitiga diketahui panjang alas dan tingginya.
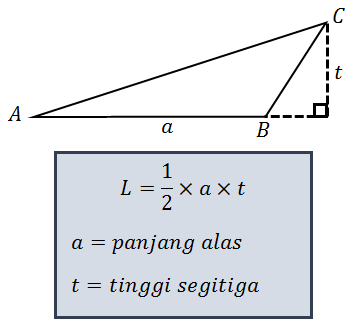
Contoh Soal
Nilai luas segitiga yang memiliki alas 12 cm dan tingginya 16 cm adalah....
Pembahasan:
Untuk menyelesaikan permasalahn tersebut, kita harus ingat
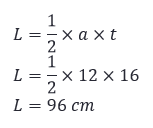
Jadi, luas segitiga adalah 96 cm.
RUMUS LUAS SEGITIGA JIKA DIKETAHUI KETIGA SISINYA
Jika sebuah segitiga diketahui panjang ketiga sisinya tanpa diketahui tinggi dapat dicari luasnya dengan rumus berikut:
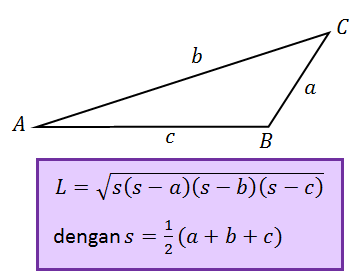
Contoh Soal
Perhatikan segitiga berikut!
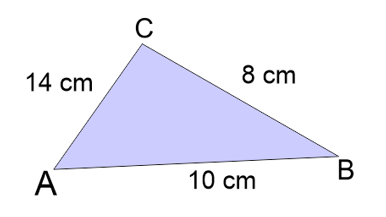
Luas segitiga adalah….
Pembahasan:
Dengan menggunakan rumus luas segitiga sebarang
Luas Segitiga Dengan Perbandingan Trigonometri
Nah selain dua rumus luas segitiga sebelumnya, kita juga dapat mencari luas segitiga jika diketahui sudutnya lho, Sobat!
Dengan menggunakan perbandingan trigonometri, kita dapat mengetahui luas segitiga sebarang. Yuk kita simak bersama!
RUMUS LUAS SEGITIGA JIKA DIKETAHUI PANJANG DUA SISI DAN BESAR SUDUT APITNYA
Jika sebuah segitiga diketahui panjang dua sisi dan besar sudut yang diapit oleh kedua sisi tersebut, kita dapat menggunakan rumus luas segitiga berikut:
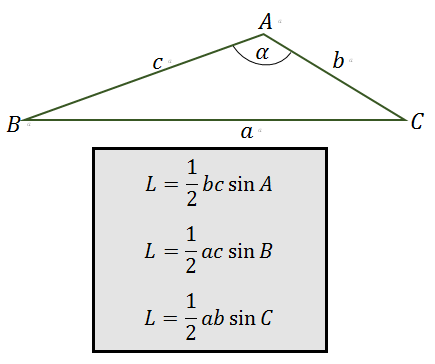
Contoh Soal
Perhatikan segitiga berikut!
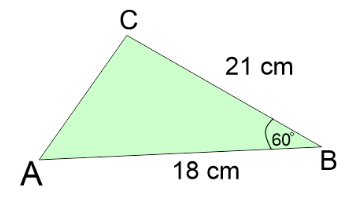
Luas segitiga ABC adalah….
Pembahasan:
Untuk mencari luas maka:
RUMUS LUAS SEGITIGA JIKA DIKETAHUI PANJANG SISI DAN DUA SUDUTNYA
Kebalikan dari rumus sebelumnya, jika diketahui besar dua sudut dan panjang sisi yang diapit kedua sudut tersebut dapat digunakan rumus luas segitiga berikut:
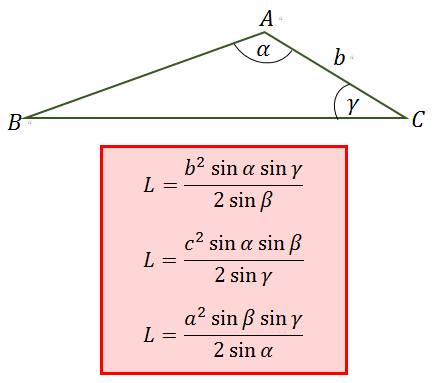
Contoh Soal
Perhatikan segitiga berikut!
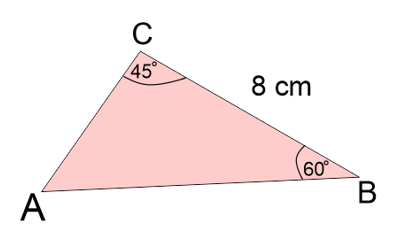
Luas segitiga ABC adalah….
Pembahasan:
Diketahui panjang BC = 8 cm
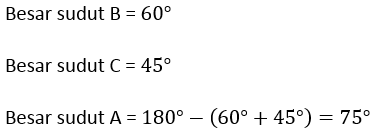
Untuk menyelesaikan luas segitiga tersebut, maka gunakan rumus:
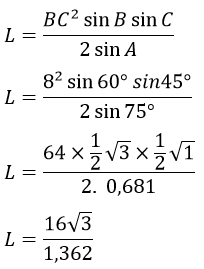
1.
Kerjakan soal berikut ini!
Diketahui segitiga ABC dengan panjang AB = 4cm, AC= 3cm, sudut A= 135o. Luas segitiga tersebut adalah ....
A.
B.
C.
D.
E.
JAWABAN BENAR
C.
PEMBAHASAN
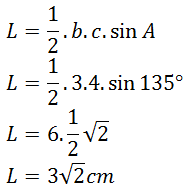
2.
Kerjakan soal berikut ini!
A. 22,5 cm
B. 20 cm
C. 18 cm
D. 15,5 cm
E. 12 cm
JAWABAN BENAR
A.
22,5 cm
PEMBAHASAN
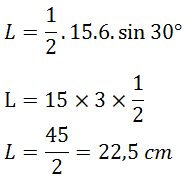
3.
Kerjakan soal berikut ini!
Diketahui segitiga ABC dengan panjang AB adalah 6 cm, BC = 8 cm. Besar sudut B, jika luas segitiga ABC = 12 cm2 adalah ....
A. 180o
B. 90o
C. 60o
D. 45o
E. 30o
JAWABAN BENAR
E.
30o
PEMBAHASAN
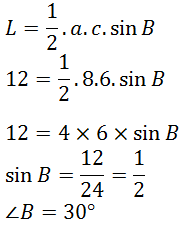
4.
Kerjakan soal berikut ini!
A. 0o
B. 30o
C. 45o
D. 60o
E. 90o
JAWABAN BENAR
D.
60o
PEMBAHASAN
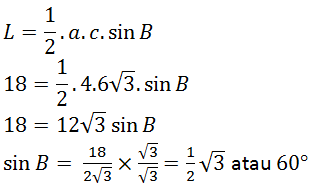
5.
Kerjakan soal berikut ini!
Luas segitiga PQR, jika diketahui panjang PQ = 5 cm, PR = 7 cm dan QR = 8 cm adalah ....
A.
B.
C.
D.
E.
JAWABAN BENAR
B.
PEMBAHASAN
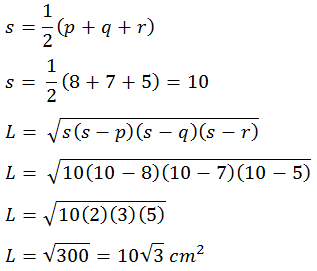
6.
Kerjakan soal berikut ini!
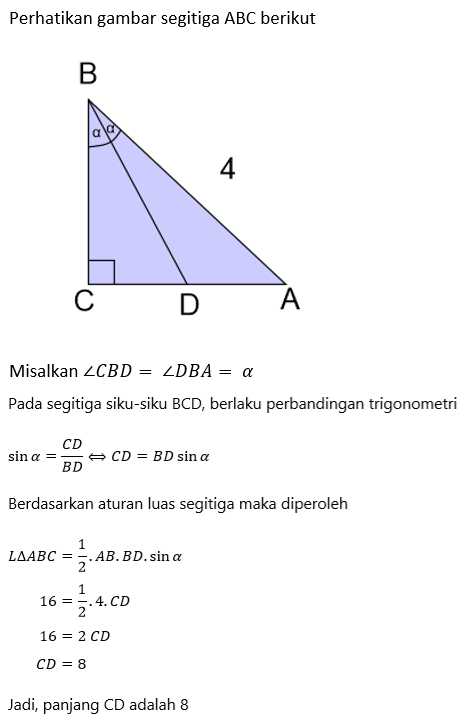
Diberikan segitiga ABC siku-siku di C. Titik D terletak pada sisi AC sedemikian sehingga garis BD membagi dua sudut ABC sama besar. Diketahui panjang AB= 4 dan luas segitiga ABD sama dengan 16. Panjang sisi CD adalah….
A. 4
B. 6
C. 8
D. 10
E. 12
JAWABAN BENAR
C.
8
PEMBAHASAN
7.
Perhatikan jajargenjang berikut ini!
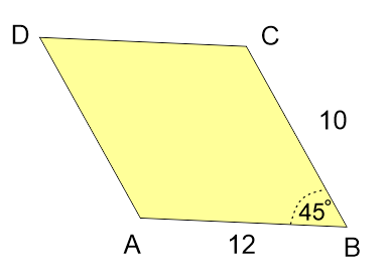
Panjang PQ adalah 12 cm dan QR adalah 10 cm. Sudut PQR adalah….
A.
B.
C.
D.
E.
JAWABAN BENAR
A.
PEMBAHASAN
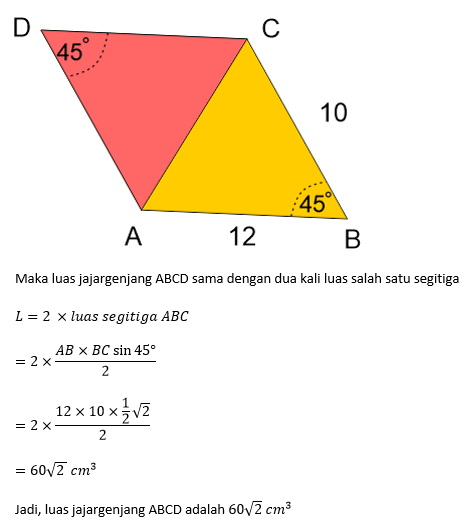
Jajar genjang tersusun dari dua buah segitiga, yaitu segitiga ABC dan segitiga ADC dengan luas yang sama
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
Ikuti Kami
Download Aku Pintar
