APSiswaNavbarV2

redesain-navbar Portlet

BelajarPintarV3

Matematika Wajib

Sistem Pertidaksamaan Linear Dua Variabel

Daftar Materi

MATERI

Konsep Sistem Pertidaksamaan Linear Kuadrat

Dalam sistem pertidaksamaan kuadrat dua variabel terdapat 2 macam sistem, yaitu

  • Sistem pertidaksamaan linear-kuadrat
  • Sistem pertidaksamaan kuadrat-kuadrat

Sistem Pertidaksamaan Linear Kuadrat

Sistem pertidaksamaan linear-kuadrat berarti suatu sistem pertidaksamaan yang terdiri atas pertidaksamaan linear dan pertidaksamaan kuadrat.
Bentuk umum Pertidaksamaan linear Kuadrat

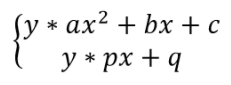
Dengan * merupakan tanda pertidaksamaan

Langkah-langkah membuat sketsa grafik sistem pertidaksamaan linear-kuadrat sebagai berikut: 

  1. Sketsa grafik masing-masing persamaan persamaan linear dan persamaan kuadrat 
  2. Beri arsiran untuk daerah penyelesaian masing-masing pertidaksamaan. 
  3. Tentukan daerah penyelesaian yang merupakan irisan atau perpotongan daerah yang memenuhi sistem pertidaksamaan terkait. 
  4. Lakukan pengujian kebenaran dengan memilih titik uji di dalam daerah penyelesaian tersebut

Konsep Sistem Pertidaksamaan Kuadrat-Kuadrat

Sistem pertidaksamaan kuadrat-kuadrat berarti suatu sistem pertidaksamaan yang terdiri atas pertidaksamaan kuadrat saja.

Bentuk umum Pertidaksamaan Kuadrat- Kuadrat

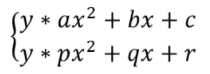
Dengan * merupakan tanda pertidaksamaan

Penyelesaian Sistem Pertidaksamaan Kuadrat -Kuadrat

Sama seperti pertidaksamaan linear-kuadrat, penyelesaian dari sistem pertidaksamaan kuadrat juga berupa daerah penyelesaian.
Langkah-langkah penyelesaian dari Sistem Pertidaksamaan Kuadrat-Kuadrat yaitu :

  1. Buat sketsa grafik dari masing-masing persamaan kuadrat 
  2. Berilah arsiran untuk daerah penyelesaian masing-masing pertidaksamaan 
  3. Tentukan daerah penyelesaian yang merupakan irisan atau perpotongan dari daerah yang memenuhi sistem pertidaksamaan terkait. 
  4. Lakukan pengujian dengan menguji sembarang titik

Penyelesaian Sistem pertidaksamaan jika diketahui daerah penyelesaiannya

suatu fungsi kuadrat dapat ditentukan jika diketahui beberapa unsurnya, yaitu

  •  Jika fungsi kuadrat diketahui titik potong dengan sumbu x yaitu (x1 , 0) dan (x2 , 0) maka persamaannya adalah f(x) = a(x – x1)(x – x2)
  •  Jika suatu fungsi kuadrat diketahui titik baliknya P(p , q), maka persamaannya adalah f(x) = a(x – p)2 + q

Aturan ini dipakai untuk menyusun pertidaksamaan kuadrat jika diketahui gambar daerah penyelesaiannya.
 

1.

Jawablah soal di bawah ini dengan benar!


 


A.
B.
C.
D.
E.

JAWABAN BENAR

C.

PEMBAHASAN

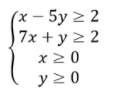
Pada x-5y=2, jika x=0, maka
0-5y=2
y=-2/5        (0,-2/5)
Pada x-5y=2, jika y=0, maka
x-5.0=2
x=2        (2,0)
Pada 7x+y=2, jika x=0, maka
7.0+y=2
y=2        (0,2)
Pada 7x+y=2, jika y=0, maka
7x+0=2
x=2/7        (2/7,0)


Sehingga diperoleh daerah penyelesaian:

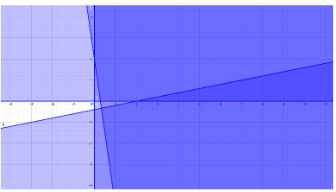
2.

Jawablah soal di bawah ini dengan benar!


 


A.
B.
C.
D.
E.

JAWABAN BENAR

A.

PEMBAHASAN

Pada x+y=8, jika x=0, maka
0+y=8
y=8        (0,8)
Pada x+y=8, jika y=0, maka
x+0=8
x=8        (8,0)
Pada x+2y=10, jika x=0, maka
0+2y=10
y=10/2=5        (0,5)
Pada x+2y=10, jika y=0, maka
x+2 .0=10
x=10        (10,0)

Sehingga diperoleh daerah penyelesaian

 

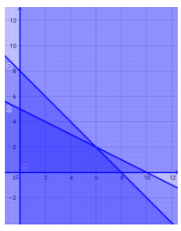
3.

Perhatikan grafik berikut!


 

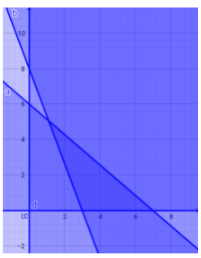
Sistem pertidaksamaan linear dua variabel dengan daerah penyelesaian pada grafik tersebut adalah ....
 


A.
B.
C.
D.
E.

JAWABAN BENAR

E.

PEMBAHASAN


 

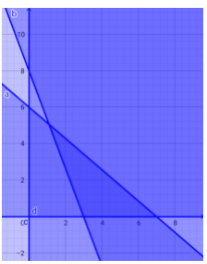
Garis a memotong sumbu x di titik (7,0) dan memotong sumbu y di titik (0,6)
Sehingga diperoleh persamaan 
6x+7y=6×7
6x+7y=42
Garis b memotong sumbu x di titik (3,0) dan memotong sumbu y di titik (0,8)
Sehingga diperoleh persamaan 
8x+3y=8×3
8x+3y=24

Menentukan simbol pertidaksamaan pada garis a dengan menguji titik (4,1)
6×4 + 7×1 ... 42
24 + 7 ... 42

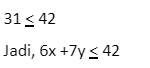
Menentukan simbol pertidaksamaan pada garis b dengan menguji titik (4,1)
8×4 + 3×1 ... 24
32 + 3 ... 24

maka tersebut merupakan salah satu pertidaksamaannya, sehingga diperoleh SPtLDV 


 

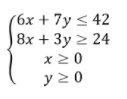
4.

Jawablah soal berikut ini!

Daerah penyelesaiannya adalah ....


A.
B.
C.
D.
E.

JAWABAN BENAR

C.

PEMBAHASAN


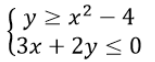
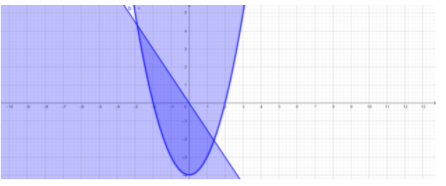
Menggambar fungsi y=x2-4
fungsi y=x2-4 merupakan fungsi kuadrat sehingga untuk menggambarkan grafiknya perlu mencari titik yang memotong sumbu x, y dan titik puncaknya, jika y=0, maka
0=x2-4
0=(x-2)(x+2)
x = 2  atau x = -2    
Sehingga grafik tersebut memotong sumbu x di dua titik yaitu (2,0) dan (-2,0)
jika x = 0 maka
y=02-4= -4 ,  maka grafik memotong sumbu y di titik (0,-4)

 

Menggambar grafik  3x+2y=0
jika y=3, maka
3x+2.3=0
x=-6/3= -2        (-2,3)

jika x=0, maka
3.0+2y=0
y=0            (0,0)


Sehingga diperoleh daerah penyelesaian


 

5.

Jawablah soal berikut ini!

Daerah penyelesaian dari sistem pertidaksamaan kuadrat-kuadrat berikut adalah ....


 


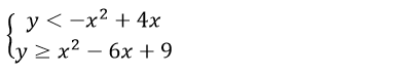
A.
B.
C.
D.
E.

JAWABAN BENAR

D.

PEMBAHASAN


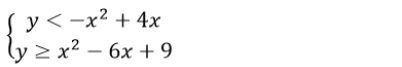
Menggambar fungsi y=-x2+4x
fungsi y=-x2+4x merupakan fungsi kuadrat sehingga untuk menggambarkan grafiknya perlu mencari titik yang memotong sumbu x, y dan titik puncaknya, jika y=0, maka
0=-x2+4x
0=x(-x+4)
x = 0  atau x = 4    
Sehingga grafik tersebut memotong sumbu x di dua titik yaitu (0,0) dan (4,0)
jika x = 0 maka
y=-02+4.0= 0, maka grafik memotong sumbu y di titik (0,0)

Menggambar grafik y=x2-6x+9
fungsi y=x2-6x+9 merupakan fungsi kuadrat sehingga untuk menggambarkan grafiknya perlu mencari titik yang memotong sumbu x, y dan titik puncaknya, jika y=0, maka
0=x2-6x+9 
0=(x-3)2
x = 3    
Sehingga grafik tersebut memotong sumbu x di satu titik yaitu (3,0)
jika x = 0 maka
y=02-6.0+9= 9,  maka grafik memotong sumbu y di titik (0,9)

 -    Menentukan daerah yang diarsir dengan menguji titik (1,0) pada y<-x2+4x
      0<-12+4.1
      0<-1+4
      0<3     (BENAR)
      Maka daerah yang diarsir adalah daerah yang memuat titik (1,0)


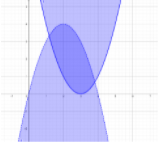
Sehingga diperoleh daerah penyelesaian

 

6.

Jawablah soal berikut ini!


 


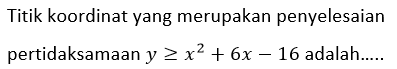
A. (-5,2)
B. (1,-10)
C. (3,5)
D. (-9,3)
E. (4,-3)

JAWABAN BENAR

A.

(-5,2)

PEMBAHASAN

Titik koordinat yang merupakan penyelesaian merupakan titik yang memenuhi pertidaksamaan
Untuk menyelesaikan soal tersebut, maka langsung saja untuk mensubstitusikan pilihannya

 Option A


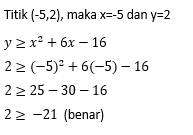
Jadi, (-5,2) merupakan penyelesaiannya

7.

Perhatikan grafik berikut!


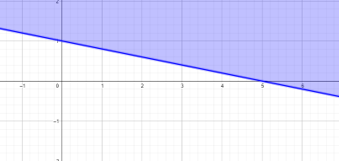
Grafik yang diarsir merupakan penyelesaian dari pertidaksamaan….


A.
B.
C.
D.
E.

JAWABAN BENAR

A.

PEMBAHASAN

Grafik garis lurus di atas memotong sumbu-x di (5,0) 
dan memotong di sumbu-y (0, 1). Maka persamaan garisnya berbentuk 

Dengan demikian, pertidaksamaan garisnya 5y+x=5

redesain-navbar Portlet