Belajar Pintar Materi SMP, SMA, SMK
BelajarPintarV3
Matematika Wajib
Trigonometri
MATERI
Ukuran Sudut


Sumber: Unsplash
Sobat Pintar pernah bermain layang-layang, bukan?
Kalian pernah menerbangkan layang-layang setinggi apa, Sobat?
Wah, pasti seru sekali kalau kita bisa tahu tinggi dari layang-layang yang kita terbangkan!
Nah, Sobat Pintar bisa menghitung tinggi layang-layang yang kalian terbangkan dengan menggunakan trigonometri, lho!
Sebelum kita membahas mengenai trigonometri, satuan yang digunakan untuk menyatakan besarnya suatu sudut itu apa ya, Sobat?
Yap! Benar sekali, seperti yang kita ketahui, satuan yang digunakan untuk menyatakan besarnya suatu sudut adalah derajat.
Namun, terdapat ukuran lain yang dapat digunakan untuk menentukan besarnya suatu sudut, yaitu radian.
Nah dalam trigonometri, kita akan menggunakan kedua ukuran tersebut, derajat dan radian, untuk menentukan besarnya suatu sudut.
Derajat yang biasa disimbolkan dengan “o”. Satu putaran penuh lingkaran sama dengan 360o atau 1o didefinisikan sebagai sudut yang dibentuk oleh 1/360 putaran penuh. Ukuran sudut yang lebih kecil dari derajat adalah menit (') dan detik (").
Hubungan ukuran sudut menit, detik, dan derajat dapat dinyatakan sebagai berikut:

Selain derajat, ukuran sudut yang lainnya adalah radian. Satu radian adalah ukuran sudut pusat lingkaran yang memotong busur yang panjangnya sama dengan radius lingkaran. Karena radius diukur dalam satuan radius (r) pada busur suatu lingkaran dan satu lingkaran penuh adalah 2.phi.r, maka dalam satu lingkaran terdapat 2phi radian
Hubungan ukuran sudut derajat dengan radian dapat dinyatakan sebagai berikut:

KONVERSI UKURAN SUDUT DERAJAT KE RADIAN
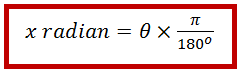
KONVERSI UKURAN SUDUT RADIAN KE DERAJAT

Agar lebih paham lagi, yuk kita simak contoh soal berikut ini!
CONTOH 1: Mengubah Radian ke Derajat
Jawablah soal di bawah ini dengan tepat!

Pembahasan
Untuk mengubah radian ke dalam derajat maka menggunakan rumus

Maka:

CONTOH 2: Mengubah Sudut ke Radian
Jawablah soal di bawah ini dengan tepat!
Besar derajat untuk sudut 70º30' adalah….
Pembahasan

Perbandingan Trigonometri

Trigonometri berasal dari bahasa yunani, yaitu trigono : tiga sudut dan metro : mengukur. Trigonometri sangat erat kaitannya dengan sudut segitiga. Istilah-istilah yang tidak akan bisa lepas dari trigonometri yaitu : sinus, cosinus, tangen, cotangen, secan, cosecan.
PERBANDINGAN TRIGONOMETRI PADA SEGITIGA SIKU-SIKU
Dalam menentukan rasio trigonometri, kita dapat menggunakan segitiga siku-siku yang diketahui panjang ketiga sisinya. Jika salah satu sisinya belum diketahui, kita harus mencari tahu terlebih dahulu panjang sisinya dengan rumus Teorema Pythagoras. Masih ingat teorema Pythagoras, Sobat?
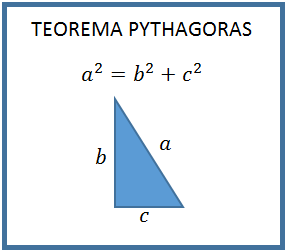
Setelah mengetahui panjang ketiga sisinya, selanjutnya kita akan membahas mengenai definisi sinus, cosinus, tangen, cotangen, secan, dan cosecan.
Coba perhatikan gambar di bawah ini!
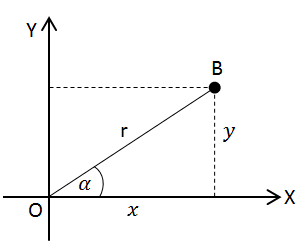
Keterangan:
OA = x = sisi siku-siku di samping sudut
AB = y = sisi siku-siku di depan sudut
OB = r = sisi miring
Berdasarkan gambar tersebut, diperoleh perbandingan sisi-sisi segitiga sebagai berikut :
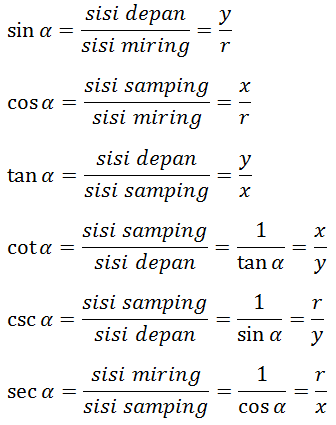
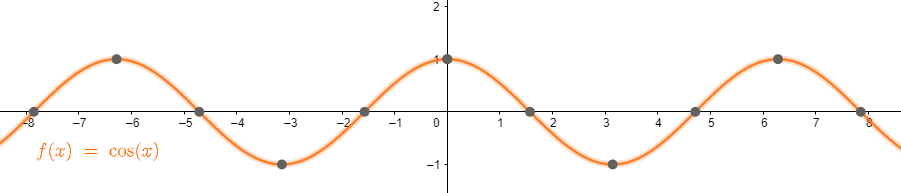
GRAFIK TRIGONOMETRI
- y= sin (x)

- y = cos (x)
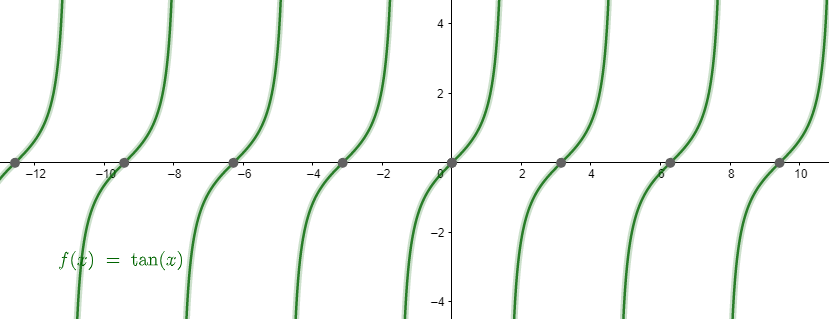
- y = tan (x)
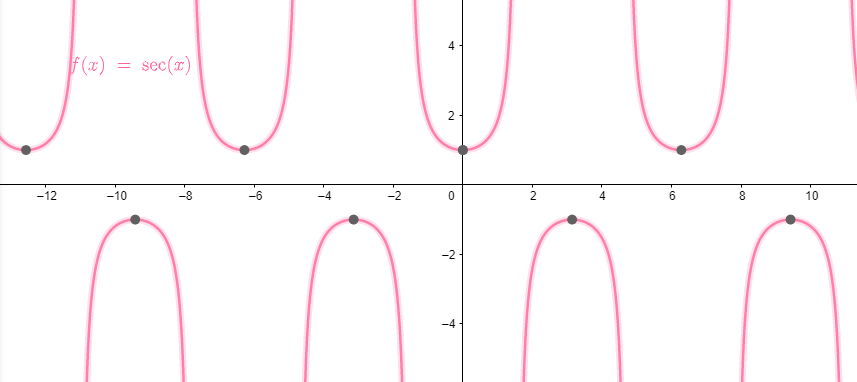
- y = sec(x)
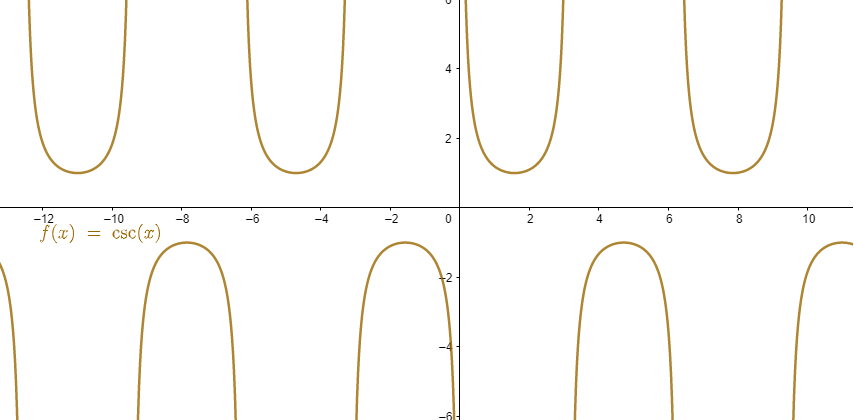
- y = csc (x)
- y = cot (x)
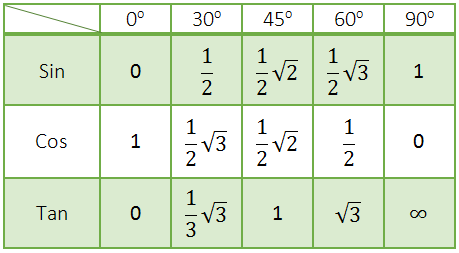
NILAI PERBANDINGAN TRIGONOMETRI SUDUT-SUDUT ISTIMEWA
PERBANDINGAN TRIGONOMETRI SUATU SUDUT DI KUADRAN I, II, III, IV
Nilai trigonometri dari suatu sudut dapat bertanda negatif bergantung pada letak kuadran sudut tersebut.
Perhatikan gambar di bawah ini!
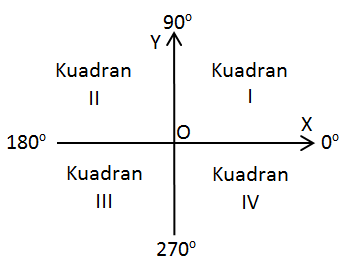
Gambar diatas merupakan pembagian kuadran pada koordinat cartesius berdasarkan sudut pada satu putaran penuh lingkaran.
Kuadran I
Perhatikan gambar di bawah ini!
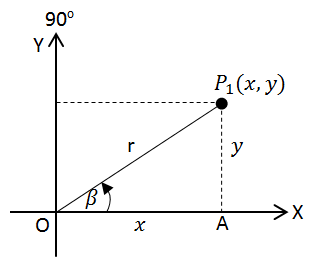
Titik P1 (x,y) terletak di kuadran I, membentuk sudut AOP1 sebesar ß.
Kuadran II
Perhatikan gambar di bawah ini!
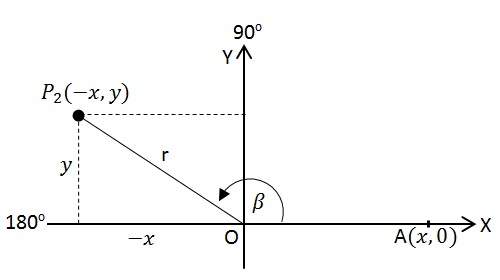
Titik P2 (-x,y) terletak di kuadran II, membentuk sudut AOP2 sebesar ß.
Kuadran III
Perhatikan gambar di bawah ini!
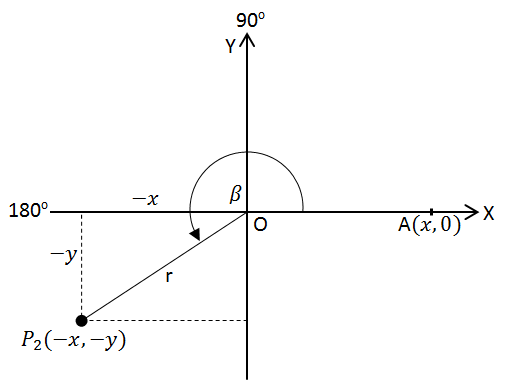
Titik P3 (-x,-y) terletak di kuadran III, membentuk sudut AOP3 sebesar ß.
Kuadran IV
Perhatikan gambar di bawah ini!
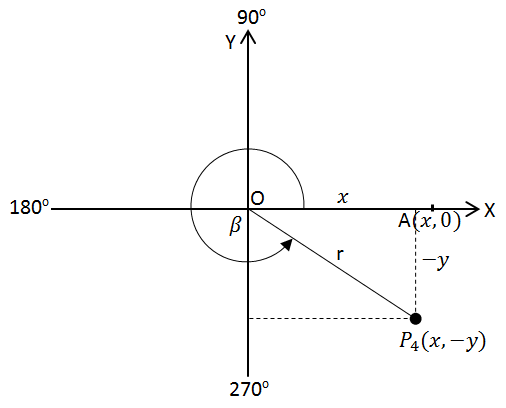
Titik P4 (x,-y) terletak di kuadran IV, membentuk sudut AOP4 sebesar ß.
Berdasarkan penjelasan di atas, dapat disimpulkan bahwa nilai sinus, cosinus, tangen, cotangen, secan, cosecan pada kuadran I, II, III, dan IV, yaitu :

Yuk! Agar lebih paham kita simak contoh soal berikut ini
Kerjakan soal berikut ini!

Pembahasan
Sebelum menentukan nilai diatas, maka kita harus mencari
panjang sisi masing-masing segitiga
Panjang AB=12
Panjang BC=15
Dengan menggunakan Pythagoras maka panjang AC adalah
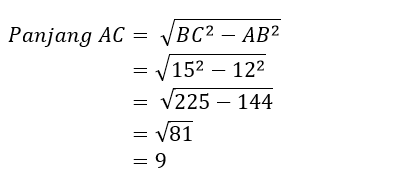
Jadi, nilai

1.
Kerjakan soal berikut ini!
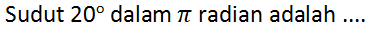
A.

B.

C.

D.

E.

JAWABAN BENAR
E.

PEMBAHASAN
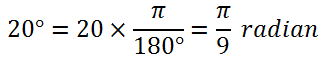
2.
Kerjakan soal berikut ini!

A. 18o
B. 15o
C. 10o
D. 8o
E. 5o
JAWABAN BENAR
A.
18o
PEMBAHASAN
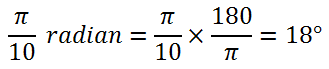
3.
Kerjakan soal berikut ini!
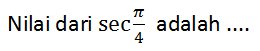
A.

B.

C.

D.

E.

JAWABAN BENAR
B.

PEMBAHASAN

4.
Kerjakan soal berikut ini!

A. 12/13
B. 13/12
C. 5/13
D. 12/5
E. 5/12
JAWABAN BENAR
D.
12/5
PEMBAHASAN
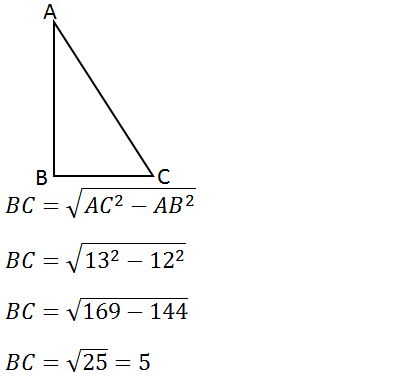
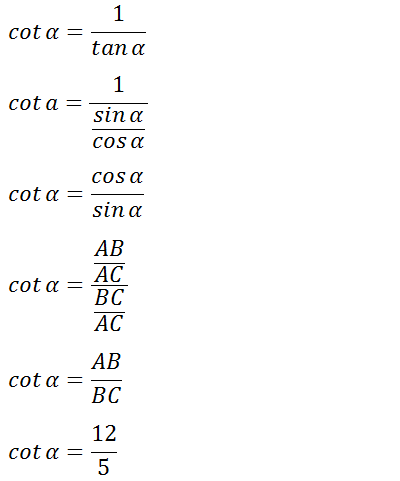
5.
Kerjakan soal berikut ini!
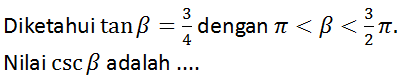
A. - 3/5
B. - 5/3
C. - 5/4
D. 3/5
E. 5/3
JAWABAN BENAR
B.
- 5/3
PEMBAHASAN
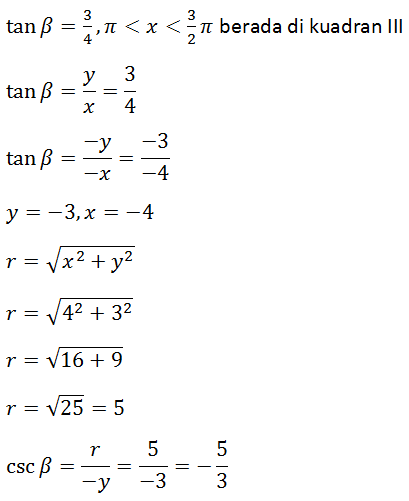
6.
Kerjakan soal berikut ini!
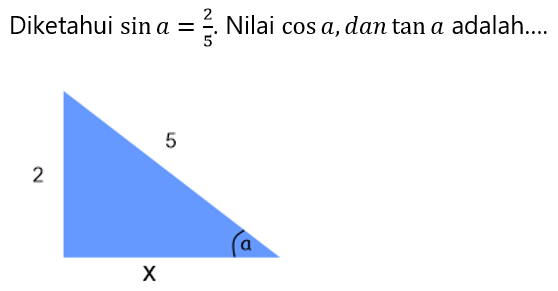
A.

B.

C.

D.

E.

JAWABAN BENAR
D.

PEMBAHASAN
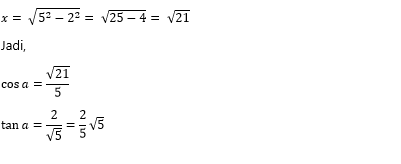
7.
Nilai dari 214º10'72''ke dalam bentuk derajat adalah….
A. 324,62°
B. 316,62°
C. 314,62°
D. 209,62°
E. 214,62°
JAWABAN BENAR
E.
214,62°
PEMBAHASAN


Oops!!!
Yah, jawaban kamu meleset nih. Ingin melihat pembahasan soal ini?

BENAR!!!
Selamat!
Jawaban kamu benar. Ingin lihat pembahasan soal ini?
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved

