APSiswaNavbarV2

redesain-navbar Portlet

BelajarPintarV3

Matematika Minat

Lingkaran

Daftar Materi

MATERI

Persamaan Garis Singgung Lingkaran

Jadi, panjang dari rantai yang dibutuhkan untuk menghubungkan engsel sepeda dengan roda belakang sepeda dapat kita cari dengan menggunakan rumus-rumus pada materi kali ini.

Langsung simak pembahasannya ya!

Sebelumnya, Sobat Pintar sudah mencari tahu kedudukan garis terhadap lingkaran, salah satunya adalah garis yang menyinggung lingkaran. Jika dalam mencari kedudukan garis terhadap lingkaran akan diketahui persamaan garisnya, pada materi kali ini kita akan mencari persamaan dari garis yang menyinggung lingkaran.

Garis singgung sendiri adalah garis yang memotong lingkaran hanya di satu titik. Dalam mencari persamaan garis singgung lingkaran, kita dapat menentukannya dengan cara-cara berikut:

PERSAMAAN GARIS SINGGUNG JIKA DIKETAHUI TITIK PADA LINGKARAN

Titik pada lingkaran dapat juga disebut dengan titik potong antara garis dengan lingkaran. Untuk menentukan persamaan garis singgung jika diketahui titik P(x1,y1) pada lingkaran dapat dicari bergantung persamaan lingkarannya, yaitu:

 

PERSAMAAN GARIS SINGGUNG JIKA DIKETAHUI GRADIENNYA

Persamaan  garis singgung lingkaran jika diketahui  gradiennya dapat ditentukan dengan rumus berikut:

 

PERSAMAAN GARIS SINGGUNG JIKA DIKETAHUI TITIK DI LUAR LINGKARAN

Terdapat 3 cara untuk menentukan persamaan garis singgung jika diketahui titik di luar lingkaran, tiga cara tersebut antara lain:

  1. Menggunakan diskriminan
  • Lakukan pemisalan persamaan garis dengan gradien m dan melalui titik A(x1, y1)
    y – y1 = m (x – x1) 
    y = mx – mx1 + y1
  • Substitusi persamaan garis tersebut ke persamaan lingkaran sehingga diperoleh persamaan kuadrat dengan variabel x
  • Karena garis menyinggung lingkaran, artinya diskriminan dari persamaan kuadrat tadi harus bernilai nol atau D = 0
  • Cari nilai m, dan kembalikan nilai m ke persamaan garis singgung pada langkah awal
  1. Menggunakan rumus persamaan garis singgung dengan gradien diketahui
  • Lakukan pemisalan persamaan garis dengan gradien m dan melalui titik A(x1, y1)
    y – y1 = m (x – x1) 
    y = mx – mx1 + y1
  • Lakukan pemisalan persamaan garis singgung lingkaran dengan gradien m
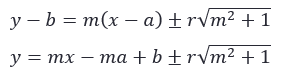
  • Samakan kedua garis singgung untuk mendapat nilai m
  • Kembalikan nilai m ke pemisalan awal
  1. Menggunakan bantuan persamaan garis kutub
  • Cari persamaan garis kutub titik A(x1, y1) dengan rumus
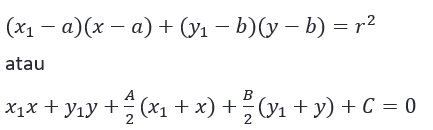
  • Substitusi persamaan garis ke kutub ke persamaan lingkaran untuk mendapatkan titik potong garis kutub dan lingkaran
  • Dari titik potong yang sudah didapatkan sobat pintar bisa menggunakan rumus garis singgung dengan titik pada lingkaran

Ketiga cara ini akan lebih mudah dipahami jika sobat pintar perhatikan contoh soal berikut:

Tentukan persamaan garis singgung pada lingkaran x2 + y2 = 25 yang melalui titik (–1, 7) di luar lingkaran!

Cara 1:

Cara 2:

Cara 3:

Garis Singgung pada Dua Lingkaran

Setelah melewati pembahasan persamaan garis singgung, sekarang muncul lagi pertanyaan baru, bagaimana kalau garis singgung tersebut menyinggung dua lingkaran sekaligus. Sebenarnya garis singgung ini sudah punya nama nih sobat pintar, yaitu garis singgung persekutuan dalam dan garis singgung persekutuan luar, apa saja bedanya, yuk kita bahas!

GARIS SINGGUNG PERSEKUTUAN LUAR 

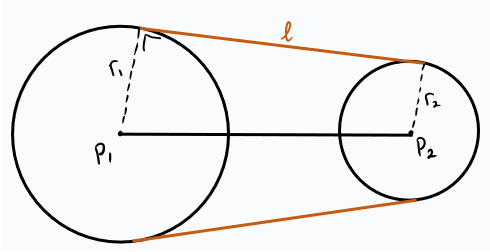
Garis singgung persekutuan luar adalah garis l yang ada pada ilustrasi di atas, sobat pintar dapat menghitung panjang ruas garisnya dengan rumus berikut.

 

GARIS SINGGUNG PERSEKUTUAN DALAM 

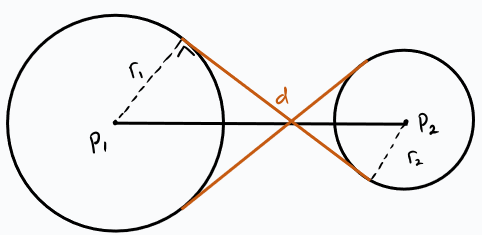
Berbeda dengan garis singgung tadi, garis singgung persekutuan dalam memiliki posisi seperti pada ilustrasi. Panjang ruas garis singgung tersebut juga bisa dihitung dengan rumus berikut.

1.

Kerjakan soal berikut ini dengan tepat!

Sebuah lingkaran memiliki persamaan x2 + y2 + 2x – 6y – 15 = 0. Jika titik (-5,6) terletak pada lingkaran, garis singgung lingkaran tersebut adalah .... 


A. 3y – 4x + 2 = 0
B. 4x – 3y + 2 = 0
C. 3x – 4y – 2 = 0
D. 4y – 3x – 2 = 0
E. 9x – 6x + 8 = 0

JAWABAN BENAR

B.

4x – 3y + 2 = 0

PEMBAHASAN

2.

Kerjakan soal berikut ini dengan tepat!

Diketahui lingkaran berpusat di O(0,0) dengan jari-jari 9 cm. Jika gradien garis singgung pada lingkaran tersebut sama dengan – ½ , maka persamaan garis singgungnya adalah ....


A.
B.
C.
D.
E.

JAWABAN BENAR

A.

PEMBAHASAN

3.

Kerjakan soal berikut ini dengan tepat!

Gradien garis singgung yang melewati titik (11,2) dan menyinggung lingkaran (x – 7)2 + (y + 1)2 = 25 adalah ....


A. 4
B. 3
C. 4/3
D. 3/4
E. 1/2

JAWABAN BENAR

C.

4/3

PEMBAHASAN

Substitusi titik (11,2) pada lingkaran (x – 7)2 + (y + 1)2 = 25 untuk mengetahui letak titik pada lingkaran

(11 – 7)2 + (2 + 1)2 = 25

(4)2 + (3)2 = 25

16+9 = 25

25 = 25 (titik terletak pada lingkaran)

Substitusi titik (11,2) pada lingkaran (x – 7)(x1 – 7) + (y + 1)(y1 + 1) = 25

(x – 7)(11 – 7) + (y + 1)(2 + 1) = 25

(x – 7)4 + (y + 1)3 = 25

4x – 28 + 3y + 3 = 25

4x + 3y = 25 + 28 – 3 

4x + 3y = 50

Gradien garis singgungnya adalah 4/3

4.

Kerjakan soal berikut ini dengan tepat!

Titik (12,5) terletak pada lingkaran x2 + y2 = 169, persamaan garis singgung yang melewati titik tersebut yaitu ....


A. x + y = 13
B. 5x – 12y = 169
C. 5x + 12y = 169
D. 12x + 5y = 169
E. 12x – 5y = 169

JAWABAN BENAR

D.

12x + 5y = 169

PEMBAHASAN

x.x1 + y.y1 = 169

x.12 + y.5 = 169

12x + 5y = 169

5.

Kerjakan soal berikut dengan tepat!

Persamaan garis singgung lingkaran x2 + y2 = 16 yang tegak lurus garis 2x – y = 8 adalah ....


A.
B.
C.
D.
E.

JAWABAN BENAR

D.

PEMBAHASAN

6.

Kerjakan soal berikut dengan tepat!

Persamaan garis singgung pada lingkaran x2 + y2 = 25 yang melalui titik T(7, 0) di luar lingkaran adalah ....


A.
B.
C.
D.
E.

JAWABAN BENAR

C.

PEMBAHASAN

7.

Kerjakan soal berikut dengan tepat!

Panjang garis singgung persekutuan dalam dua lingkaran adalah 24 cm dan jarak kedua pusatnya adalah 26 cm. jika panjang salah satu jari-jari lingkaran 6 cm, maka panjang jari-jari lingkaran yang lain adalah ... cm.


A. 2
B. 3
C. 4
D. 5
E. 6

JAWABAN BENAR

C.

4

PEMBAHASAN

8.

Kerjakan soal berikut dengan tepat!

Jari-jari lingkaran dengan pusat A dan B adalah 10 cm dan 4 cm. Jika panjang AB sama dengan 10 cm, maka panjang ruas garis singgung persekutuan luar dari dua lingkaran tersebut adalah ... cm.


A. 4
B. 5
C. 6
D. 7
E. 8

JAWABAN BENAR

E.

8

PEMBAHASAN

redesain-navbar Portlet