Belajar Pintar Materi SMP, SMA, SMK
BelajarPintarV3
Matematika Wajib
Barisan dan Deret
MATERI
Pertumbuhan dan Peluruhan

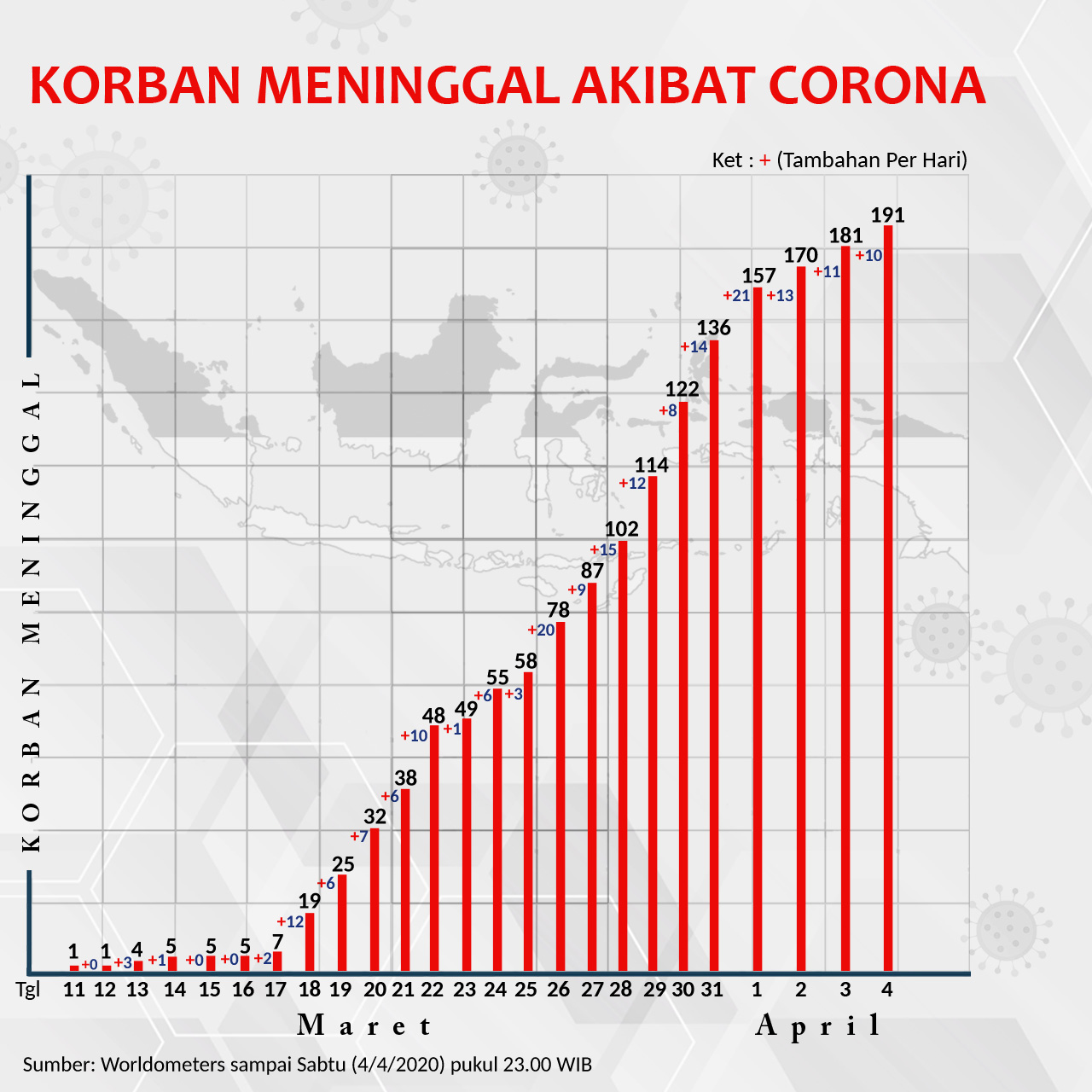
Menurut Sobat Pintar, semenjak adanya pandemi covid-19 membuat tingkat kematian penduduk Indonesia menjadi semakin bertambah atau berkurang ya? Atau bahkan semakin banyak bayi yang lahir saat pandemi ini berlangsung?
Nah suatu barisan sendiri dapat bermanfaat untuk menghitung tingkat kematian maupun kelahiran penduduk Indonesia lho, Sobat!
Kita bisa mengetahui kematian atau kelahiran mengalami pertumbuhan atau peluruhan. Seperti materi yang akan kita bahas kali ini, salah satu aplikasi dari barisan adalah mengenai pertumbuhan dan peluruhan.
Yuk, langsung simak pembahasannya ya!
PERTUMBUHAN
Pertumbuhan merupakan konsep barisan aritmetika maupun geometri yang naik, dapat dituliskan:
U1 < U2 < U3 < U4 < ... < Un
Rumus untuk menentukan pertumbuhan setelah tahun ke-n, yaitu:
- Jika diketahui persentase (i): An = Ao (1+i)n
- Jika diketahui rasio: An = Ao(r)n dengan r > 1
Keterangan:
Ao = Jumlah objek awal
An = Jumlah objek setelah tahun ke-n
i = persentase pertumbuhan
r = rasio pertumbuhan
n = periode waktu.
PELURUHAN
Peluruhan merupakan konsep barisan aritmetika maupun geometri yang turun, dapat dituliskan:
U1 > U2 > U3 > U4 > ... > Un
Rumus untuk menentukan peluruhan setelah tahun ke-n, yaitu:
An = Ao ( 1 – i )n
Khusus untuk menentukan peluruhan dari radioaktif, digunakan rumus:
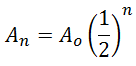
Keterangan
An = Jumlah objek setelah periode ke-n
Ao = Jumlah objek awal
i = persentase peluruhan
n = periode waktu.
Bunga Majemuk

Bunga majemuk sering kita jumpai dalam bidang perbankan. Berbeda dengan bunga tunggal, nilai dari bunga majemuk diperoleh dari nilai modal dengan bunga sebelumnya.
Rumus untuk menentukan modal akhir dengan bunga majemuk, yaitu:
Mn = Mo(1+i)n
Keterangan:
Mn = Modal akhir setelah tahun ke-n
Mo = Modal awal
i = persentase bunga majemuk
n = periode bunga majemuk.
Anuitas
Anuitas sering digunakan dalam sistem angsuran kredit (bank, rumah, kendaraan bermotor). Terdapat dua jenis anuitas, yaitu:
- Anuitas pasti, terdapat pada sistem perbankan
- Anuitas tidak pasti, terdapat pada sistem asuransi
Rumus yang digunakan untuk menentukan besarnya anuitas, yaitu:
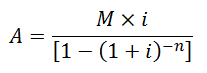
Keterangan:
A = Anuitas
M = Modal Pinjaman
i = persentase suku bunga
n = periode pinjaman.
1.
Jawablah soal berikut!
Berdasarkan survei, populasi hewan A bertambah 2% dari populasi sebelumnya setiap 3 tahun. Jika pada tahun 2020 populasi hewan A sebanyak 500 ekor, berapakah populasi hewan tersebut pada 15 tahun yang akan datang?
A. 563
B. 552
C. 541
D. 530
E. 520
JAWABAN BENAR
B.
552
PEMBAHASAN
Ao = 500
i = 2%
n = 15/3 = 5
Jadi dapat ditentukan banyaknya hewan tersebut setelah 18 tahun, yaitu:
An = Ao (1+i)n
An = 500 (1+0,02)5
An = 500 (1,02)5
An = 552 ekor
2.
Jawablah soal berikut!
Suatu unsur radioaktif meluruh dalam waktu 72 hari dengan waktu paruh 12 hari, massa awal unsur tersebut jika massa yang tersisa 10 gram adalah ....
A. 120 gram
B. 240 gram
C. 360 gram
D. 640 gram
E. 720 gram
JAWABAN BENAR
D.
640 gram
PEMBAHASAN
Menggunakan rumus peluruhan radioaktif
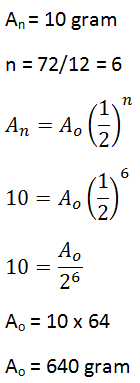
3.
Jawablah soal berikut!
Bintang membeli rumah dengan menggunakan sistem anuitas pada pembayaran kreditnya. Harga rumah tersebut adalah Rp 500.000.000,- dengan suku bunga 3% per tahun. Bintang berniat melunasi kreditnya dengan 10 kali anuitas. Besar anuitas yang harus dibayar Bintang adalah ....
A. Rp 58.616.647,-
B. Rp 43.615.253,-
C. Rp 11.161.408,-
D. Rp 5.158.745,-
E. Rp 3.838.500,-
JAWABAN BENAR
A.
Rp 58.616.647,-
PEMBAHASAN
Diketahui
Mo = 500.000.000
n = 10
i = 3% = 0,03
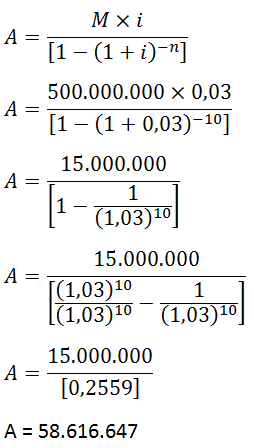
4.
Jawablah soal berikut!
Suatu neutron dapat dipecah menjadi proton dan elektron. Seorang peneliti memiliki 100.000 neutron, setelah 5 menit ia mengamati kembali neutron tersebut. Jika 10% dari neutron tersebut berubah pada akhir satu menit, jumlah neutron ketika diamati kembali oleh peneliti adalah ....
A. 2.476.099
B. 161.051
C. 59.049
D. 32.467
E. 1
JAWABAN BENAR
C.
59.049
PEMBAHASAN
Menggunakan rumus peluruhan
Diketahui
Ao = 100.000
i = 10%
n = 5
An = Ao (1 – i)n
An = 100.000 ( 1 – 0,1)5
An = 100.000 (0,9)5
An = 59049
5.
Jawablah soal berikut!
Indah menabung di sebuah bank sebesar Rp 20.000.000 dan memperoleh bunga 2,5% per tahun. Jika Indah tidak pernah menarik uang di bank selama 5 tahun, maka bunga yang diperoleh Indah dalam kurun waktu tersebut yaitu ....
A. Rp 61.035.156,-
B. Rp 41.035.156,-
C. Rp 22.628.164,-
D. Rp 22.081.616,-
E. Rp 2.628.164,-
JAWABAN BENAR
E.
Rp 2.628.164,-
PEMBAHASAN
Menggunakan rumus bunga majemuk
Diketahui
Mo = 20.000.000
i = 2,5%
n = 5
Mn = Mo (1+i)n
Mn = 20.000.000 (1+0,025)5
Mn = 20.000.000 (1,025)5
Mn = 22.628.164
Jadi, bunga yang diperoleh Indah adalah 22.628.164 – 20.000.000 = Rp 2.628.164,-
6.
Jawablah soal berikut!
Hasil produksi pakaian seragam sekolah putih abu-abu yang dibuat oleh siswa-siswa SMK Jurusan Tata Busana pada bulan pertama menghasilkan 40 setel. Setiap bulan berikutnya, hasil produksi meningkat sebanyak 5 setel sehingga membentuk deret aritmetika. Banyak hasil produksi selama 2 bulan pertama adalah ... setel.
A. 65
B. 70
C. 75
D. 80
E. 85
JAWABAN BENAR
E.
85
PEMBAHASAN
Ini merupakan kasus barisan aritmetika (karena terdapat penambahan hasil produksi yang tetap/konstan setiap bulan).
Diketahui a = 40 dan b = 5.
Jumlah pakaian seragam sekolah putih abu-abu yang diproduksi selama2 bulan pertama adalah

Jadi, jumlah/banyaknya seragam yang diproduksi selama 2 bulan adalah 85 setel.
7.
Jawablah soal berikut!
Sebuah perusahaan pada bulan pertama memproduksi 1000 unit barang dan menaikkan produksinya tiap bulan sebanyak 400 unit. Jumlah barang yang diproduksi selama satu semester adalah ....
A. 12000
B. 10000
C. 8000
D. 6000
E. 4000
JAWABAN BENAR
A.
12000
PEMBAHASAN
Ini merupakan kasus barisan aritmetika (karena terdapat penambahan produksi yang tetap/konstan setiap bulan).
Diketahui a=1000 dan b=400.
Jumlah barang yang diproduksi selama satu semester (6 bulan) adalah


Oops!!!
Yah, jawaban kamu meleset nih. Ingin melihat pembahasan soal ini?

BENAR!!!
Selamat!
Jawaban kamu benar. Ingin lihat pembahasan soal ini?
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved

