Belajar Pintar Materi SMP, SMA, SMK
BelajarPintarV3
Matematika Wajib
Barisan dan Deret
MATERI
Barisan Geometri

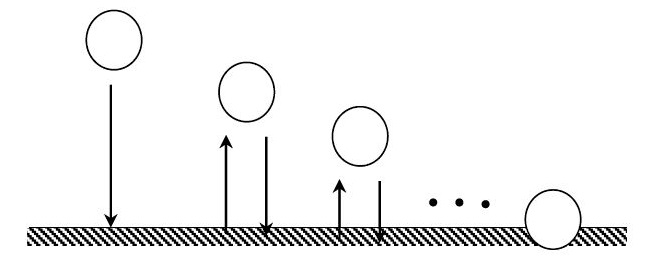
Sumber : materimatematika.com
Bola yang memantul semakin lama tinggi pantulannya akan semakin berkurang, hal ini akan membentuk sebuah pola barisan geometri lho, Sobat Pintar!
Jadi barisan geometri sendiri itu apa sih?
Yuk, langsung simak pembahasannya ya!
Barisan Geometri adalah barisan bilangan dimana dua suku yang berurutan memiliki perbandingan yang bernilai tetap. Perbandingan dalam barisan geometri disebut rasio (r).
Barisan geometri dapat dinyatakan sebagai berikut:
Un = a.rn-1
Keterangan :
Un = suku ke-n
a = suku pertama
r = rasio
n = banyaknya suku
Rasio dari barisan geometri dapat dicari dengan cara:
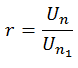
Deret Geometri
Selain barisan, terdapat juga deret geometri. Deret geometri adalah jumlah suku-suku dari suatu barisan geometri.
Sama seperti deret aritmetika, deret geometri jika dinyatakan yaitu :
U1 + U2 + U3 + U4 + ...
Rumus yang digunakan untuk menentukan jumlah n suku dari deret geometri, yaitu:
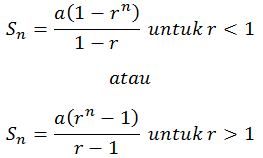
Keterangan:
Sn = jumlah n suku pertama
a = suku pertama
r = rasio
n = banyaknya suku.
Contoh soal :
Mencari suku ke-n
Diketahui barisan geometri seperti berikut : 2, 4, 16, ... .
Tentukan suku kelima dari barisan di atas!
Jawab:
Diketahui : a = 2 dan r = 2.
Un = a(rn-1)
U5 = 2(25-1)
U5 = 2(24)
U5 = 32
Mencari jumlah suku ke-n
Diketahui deret geometri seperti berikut : 3 + 9 + 27 + ... .
Tentukan jumlah 5 suku pertama dari deret di atas!
Jawab:
Diketahui : a = 3 dan r = 3.

Deret Geometri Tak Hingga

Berbeda dengan deret geometri sebelumnya yang memiliki banyak suku yang berhingga, deret geometri tak hingga merupakan penjumlahan dari suku-suku pada barisan geometri dengan rasio tertentu yang banyak sukunya tak terhitung.
Rumus untuk menentukan jumlah deret geometri tak hingga, yaitu:
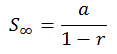
Suatu deret geometri tak hingga akan konvergen jika memiliki jumlah untuk -1 < r < 1.
- Jika diketahui suatu deret a + ar2 + ar4 + ... maka jumlah suku-suku pada kedudukan ganjil, yaitu:
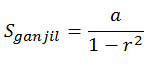
- Jika diketahui suatu deret a + ar3 + ar5 + ... maka jumlah suku-suku pada kedudukan genap, yaitu:
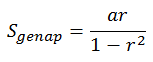 .
.
Contoh soal :
Diketahui suku pertama deret geometri adalah 49 dan jumlah tak hingga dari deret tersebut adalah 21, tentukan rasionya!
Jawab :

Suku Tengah dan Sisipan Bilangan pada Barisan Geometri

Rumus yang digunakan untuk menentukan suku tengah dari barisan geometri, yaitu:
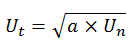
Jika pada barisan geometri disisipkan k bilangan maka akan diperoleh rasio yang baru, yaitu:
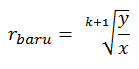
dengan x dan y adalah dua bilangan yang akan disisipkan k buah bilangan.
1.
Jawablah soal berikut!
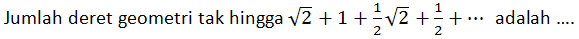
A.

B.

C.

D.

E.

JAWABAN BENAR
C.

PEMBAHASAN

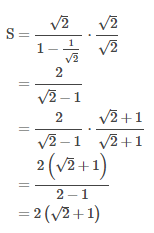
2.
Jawablah soal berikut!
Barisan geometri dengan suku ke-5 adalah 1/3 dan rasio = 1/3, maka suku ke-9 barisan geometri tersebut adalah ….
A. 27
B. 9
C. 1/27
D. 1/81
E. 1/243
JAWABAN BENAR
E.
1/243
PEMBAHASAN
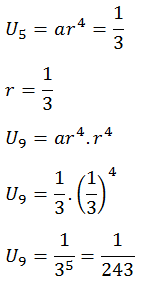
3.
Jawablah soal berikut!
Suku pertama pada barisan geometri adalah 1600. Jika suku ketiga pada barisan tersebut adalah 25, maka rasionya yaitu ....
A. 1/8
B. 1/4
C. 1/3
D. 1/2
E. 2/3
JAWABAN BENAR
A.
1/8
PEMBAHASAN
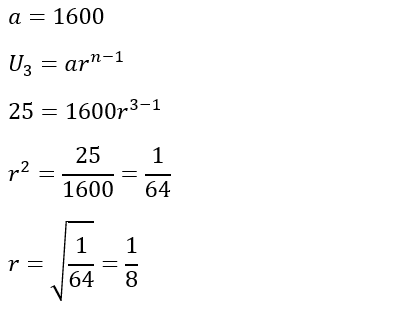
4.
Jawablah soal berikut!
Pada deret geometri 400+200+100+ ... + ... . Berapa jumlah 5 suku pertama deret geometri tersebut ....
A. 25
B. 75
C. 100
D. 550
E. 775
JAWABAN BENAR
E.
775
PEMBAHASAN
a = 400
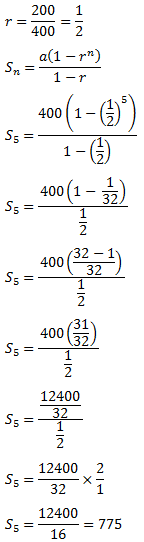
5.
Jawablah soal berikut!
Penularan virus corona pada hari ke 5 setelah masuk ke suatu negara berjumlah 12500. Apabila setiap harinya terdapat lima kali lipat jumlah oraang yang terpapar virus tersebut, maka setelah satu minggu, jumlah orang yang terpapar virus tersebut adalah ....
A. 1.562.500
B. 312.500
C. 156.250
D. 78.125
E. 62.500
JAWABAN BENAR
B.
312.500
PEMBAHASAN

6.
Jawablah soal berikut!
Hasil jumlah dari 8 + 4 + 2 +1 + ... adalah ....
A. 8
B. 16
C. 24
D. 32
E. 40
JAWABAN BENAR
B.
16
PEMBAHASAN

7.
Jawablah soal berikut!
Diketahui barisan geometri dengan suku pertama adalah 2 dan suku ke-3 adalah 8, suku ke- 5 barisan tersebut adalah ....
A. 32
B. 64
C. 128
D. 256
E. 512
JAWABAN BENAR
E.
512
PEMBAHASAN
Mencari rasio barisan geometri dari suku yang diketahui,
U1 = 2
a = 2.
U3 = 8
a.rn-1 = 8
2.r2-1 = 8
r = 4.
Suku ke-5 barisan tersebut,
U5 = a . rn-1 = 2 . 45-1 = 2 . 44 = 2 . 256 = 512.

Oops!!!
Yah, jawaban kamu meleset nih. Ingin melihat pembahasan soal ini?

BENAR!!!
Selamat!
Jawaban kamu benar. Ingin lihat pembahasan soal ini?
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved

