Matematika Wajib

Konsep Pola Bilangan

^{Sumber : lingkarwarna.com}

Pernahkah Sobat Pintar mengamati urutan nomor rumah di kompleks rumah kalian?

Apakah nomor rumahnya berpola bilangan asli sesuai urutan, atau rumah sebelah kiri menggunakan nomor rumah ganjil dan sebelah kanan menggunakan nomor rumah genap?

Nah! Materi yang akan kita bahas kali ini berhubungan dengan pola pada bilangan.

Pengertian Pola Bilangan

Pola bilangan yaitu aturan yang digunakan untuk membuat suatu kelompok bilangan.

Macam-macam Pola Bilangan

Pola bilangan dapat dikelompokkan menjadi beberapa macam, diantaranya:

Pola Bilangan Ganjil

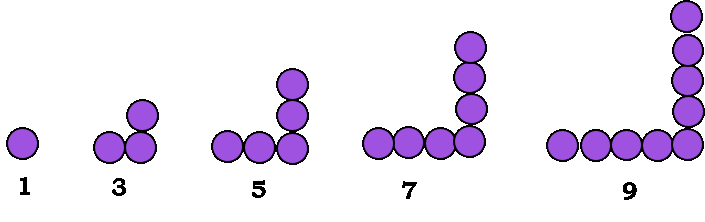
Berdasarkan pola di atas, terbentuk pola bilangan ganjil yaitu: 1, 3, 5, 7, 9.

Rumus bilangan ke-n pada pola bilangan ganjil, yaitu: 2n – 1.

Sedangkan jumlah n bilangan ganjil pertama, yaitu: n².

Pola Bilangan Genap

Berdasarkan pola di atas, terbentuk pola bilangan genap yaitu: 2, 4, 6, 8. 

Rumus bilangan ke-n pada pola bilangan genap, yaitu: 2n. 

Sedangkan jumlah n bilangan genap pertama, yaitu: n(n+1). 

Pola Garis Lurus

Pola garis lurus yaitu suatu bilangan yang digambarkan dengan noktah mengikuti pola garis lurus.

Contoh :

Pola Persegi Panjang

Berdasarkan pola di atas, terbentuk pola persegi panjang dengan susunan bilangan 2, 6, 12, 20. 

Rumus bilangan ke-n pada pola persegi panjang, yaitu: n(n+1). 

Sedangkan jumlah n suku pertamanya, yaitu:

Pola Persegi

Berdasarkan pola di atas, terbentuk pola persegi panjang dengan susunan bilangan 2, 6, 12, 20. 

Rumus bilangan ke-n pada pola persegi panjang, yaitu: n². 

Sedangkan jumlah n suku pertamanya, yaitu:

Pola Segitiga

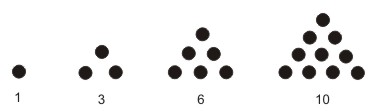
Berdasarkan pola di atas, terbentuk pola segitiga  dengan susunan bilangan 2, 6, 12, 20. 

Rumus bilangan ke-n pada pola persegi panjang, yaitu: 

Sedangkan jumlah n suku pertamanya, yaitu:

Pola Segitiga Pascal

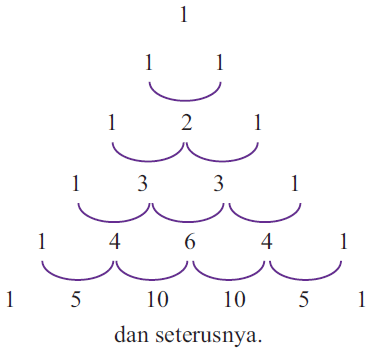
Pola di atas merupakan pola dari segitiga pascal. Segitiga pascal digunakan untuk menentukan koefisien dari polinomial. 

Koefisiennya dapat ditentukan dengan rumus : (a+b)ⁿ. 

Sedangkan jumlah bilangan pada segitiga pascal baris ke-n, yaitu: 2^n-1.