Belajar Pintar Materi SMP, SMA, SMK
BelajarPintarV3
Matematika Wajib
Integral
MATERI
Aplikasi Integral

Kalau salah satu aplikasi dari turunan adalah kecepatan dan percepatan, menurut kalian aplikasi dari antiturunan atau integral itu apa, Sobat?
Nah, aplikasi dari integral dalam kehidupan sehari-hari antara lain:
PERSAMAAN GERAK LURUS BERATURAN
Konsep integral tak tentu dapat digunakan dalam menentukan persamaan gerak lurus beraturan, yaitu:
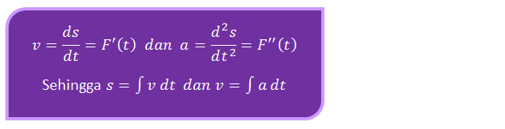
PERSAMAAN KURVA
Diketahui gradien garis singgung dengan kurva y = f(x) adalah m = f’(x), sehingga persamaan kurvanya dapat ditentukan dengan persamaan berikut :

1.
Jawablah soal berikut!
Jika f'(x)=(6x+3)2 dan f(2)=153, maka f(x) adalah ....
A. f(x)= 4x3 + 3x2 + 3x + 11
B. f(x)= 4x3 - 3x2 + 3x + 1
C. f(x)= 4x3 + 3x2 - 3x + 1
D. f(x)= 4x3 - 3x2 - 3x + 11
E. f(x)= 3x3 + 4x2 + 3x + 11
JAWABAN BENAR
A.
f(x)= 4x3 + 3x2 + 3x + 11
PEMBAHASAN
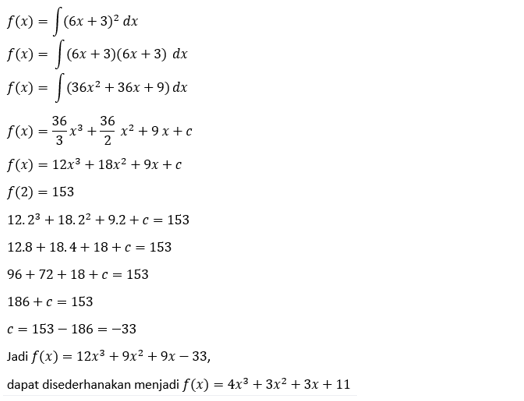
2.
Jawablah soal berikut!
Jika garis singgung kurva adalah 6x+5 yang melalui titik (1,-2) maka persamaan kurvanya adalah ....
A. f(x) = 3x2 - 5x - 10
B. f(x) = 3x2 + 5x - 10
C. f(x) = -5x2 + 3x - 10
D. f(x) = 5x2 + 3x - 10
E. f(x) = 3x2 + 5x + 10
JAWABAN BENAR
B.
f(x) = 3x2 + 5x - 10
PEMBAHASAN

3.
Jawablah soal berikut!
Pada interval 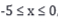 luas daerah di bawah kurva y = x2 dan di atas garis y = kx sama dengan luas daerah, di atas kurva y = x2 dan di bawah garis y = kx. Nilai k = ....
luas daerah di bawah kurva y = x2 dan di atas garis y = kx sama dengan luas daerah, di atas kurva y = x2 dan di bawah garis y = kx. Nilai k = ....
A.
B.
C.
D.
E.
JAWABAN BENAR
A.
![]()
PEMBAHASAN
Menyamakan kedua fungsinya,
y = y
x2 = kx
x2 - kx = 0
x(x-k) = 0
x = 0 atau x = k
Luas daerah arsiran pada selang (-5, k) sama dengan luas daerah arsiran pada selang (k, 0). Dengan menggunakan integral tentu,
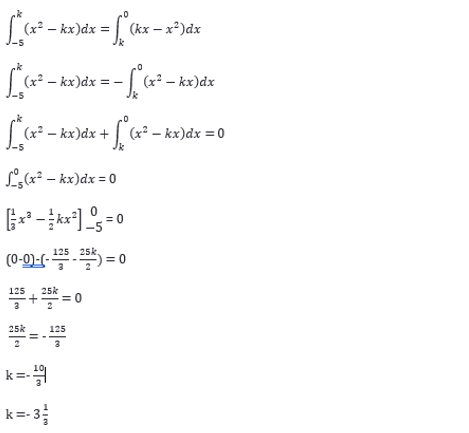
4.
Jawablah soal berikut!
Jika f'(x)=(4x+2)2 dan f(2)=60, maka nilai C dari f(x) adalah ....
A.
B.
C.
D.
E.
JAWABAN BENAR
B.
![]()
PEMBAHASAN

5.
Jawablah soal berikut!
Jika garis singgung kurva adalah 2x+1 yang melalui titik (1,1) maka persamaan kurvanya adalah ....
A. f(x) = 2x2 + x + 1
B. f(x) = 2x2 + x – 1
C. f(x) = x2 + x + 1
D. f(x) = x2 + x – 1
E. f(x) = x2 – 1
JAWABAN BENAR
D.
f(x) = x2 + x – 1
PEMBAHASAN


Oops!!!
Yah, jawaban kamu meleset nih. Ingin melihat pembahasan soal ini?

BENAR!!!
Selamat!
Jawaban kamu benar. Ingin lihat pembahasan soal ini?
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved

