Belajar Pintar Materi SMP, SMA, SMK
BelajarPintarV3
Matematika Wajib
Matriks
MATERI
Penjumlahan dan Pengurangan Matriks
Ternyata matriks juga dapat dioperasikan lho, Sobat. Operasi aljabar pada matriks hanya sebatas penjumlahan, pengurangan, perkalian dan ada juga operasi aljabar khusus yang hanya diterapkan pada matriks. Operasi apa itu? Simak sampai selesai ya!
Penjumlahan Matriks
Jika terdapat dua matriks, misal matriks A dan B, yang memiliki ordo sama, maka elemen-elemen yang seletak dapat dijumlahkan. Jumlah A dan B dapat dinyatakan dengan A+B.
Contoh :
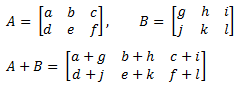
Jika A, B, C merupakan matriks dengan ordo yang sama, maka berlaku sifat penjumlahan, yaitu:
- Komutatif : A+B = B+A
- Asosiatif : (A+B)+C = A+(B+C)
- Identitas : A+O = O+A = A, dengan O adalah matriks nol
- (A+B)t = At + Bt
Pengurangan Matriks
Jika terdapat dua matriks, misal matriks A dan B, yang memiliki ordo sama, maka elemen-elemen yang seletak dapat dikurangkan. Pengurangan A dan B dapat dinyatakan dengan A – B atau A + (– B).
Contoh :
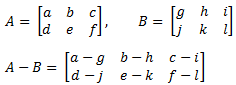
Jika A, B, C merupakan matriks dengan ordo yang sama, maka berlaku sifat pengurangan, yaitu:
- A – A = O, dengan O adalah matriks nol
- Identitas : A – O = A
- (A – B)t = At – Bt
Perkalian Matriks

Yuk kita lanjutkan dengan operasi perkalian pada matriks!
Perkalian Skalar pada Matriks
Jika diketahui A merupakan suatu matriks dan K merupakan bilangan real, maka hasil perkalian K dengan matriks A adalah matriks yang diperoleh dengan mengalikan setiap elemen A dengan K. Misalnya,
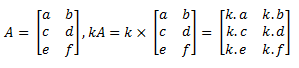
Apabila A dan B merupakan matriks dengan ordo yang sama dan k, m merupakan bilangan real, maka berlaku:
- (k+m)A = k.A + m.A
- k(A+B) = k.A + k.B
- (-1)A = A (-1) = -A, dengan –A adalah negatif dari matriks A
- k(m.A) = (k.m)A
- (kA)t = k . At
Perkalian Antar Matriks
Dua buah matriks, misal matriks A dan B, dapat dikalikan jika banyaknya kolom matriks A sama dengan banyaknya baris matriks B. Bentuk perkalian antar matriks secara umum, yaitu:
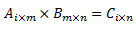
Untuk mencari hasil kali matriks A dengan matriks B ialah mengalikan elemen pada baris-baris matriks A dengan elemen pada kolom-kolom matriks B kemudian jumlahkan hasil perkalian antara baris dan kolom tersebut.
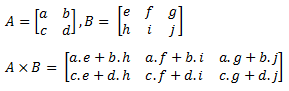
Pemangkatan Matriks
Pemangkatan matriks hanya berlaku pada matriks persegi. Jika A merupakan matriks persegi dan n, x, y adalah bilangan bulat maka berlaku:
- AxAy = A(x+y)
- (Ax)y = Ax.y
- An = A.An-1 , dengan n>0
- A0 = 1
Transpose Matriks

Nah! Ini dia operasi aljabar yang hanya berlaku pada matriks, Sobat. Menurut kalian transpose itu apa ya artinya?
Transpose suatu matriks, misal matriks A, yang dilambangkan dengan At adalah sebuah matriks yang disusun dengan cara menukarkan baris matriks A menjadi kolom matriks At dan kolom matriks A menjadi baris matriks At.
Contoh :
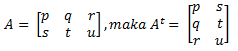
1.
Jawablah soal berikut ini!
Diketahui dua buah matriks:
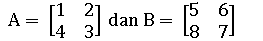
Tentukan nilai dari 3A - 2B = ….
A.

B.

C.

D.

E.

JAWABAN BENAR
A.

PEMBAHASAN
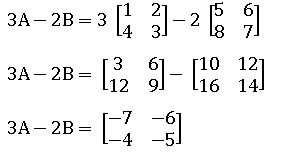
2.
Jawablah soal berikut ini!
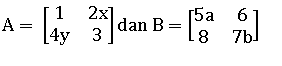
Jika A = B maka nilai dari a + x + y adalah ….
A. 6,5
B. 5,2
C. 5
D. 3
E. 2,5
JAWABAN BENAR
B.
5,2
PEMBAHASAN
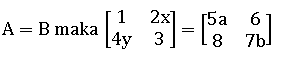
1 = 5a sehingga a = 1/5 = 0,2
2x = 6 maka x = 6/2 = 3
4y = 8 maka y = 8/4 = 2
3 = 7b maka b = 3/7
Sehingga:
a + x + y = 0,2 + 3 + 2 = 5,2
3.
Jawablah soal berikut ini!
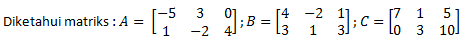
Matriks 2A + 3B – C yaitu ....
A.

B.

C.

D.

E.

JAWABAN BENAR
E.

PEMBAHASAN
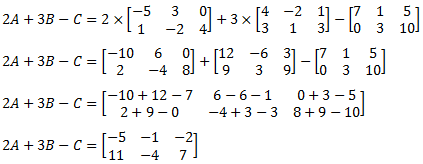
4.
Jawablah soal berikut ini!
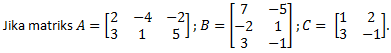
Hasil perkalian matriks A x 2B x C adalah ....
A.

B.

C.

D.

E.

JAWABAN BENAR
D.

PEMBAHASAN
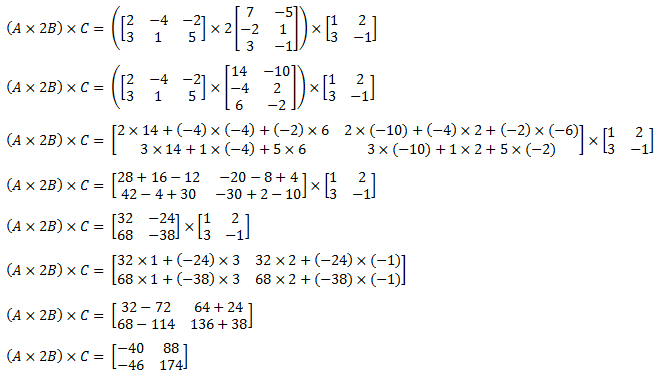
5.
Jawablah soal berikut ini!
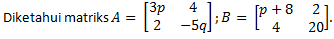
Jika A=Bt maka nilai p+q adalah ....
A. -4
B. 4
C. 0
D. -3
E. -8
JAWABAN BENAR
C.
0
PEMBAHASAN
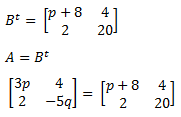
Dapat diperoleh sebagai berikut
3p=p+8
3p-p=8
2p=8
p=8/2=4
-5q=20
q=20/(-5)= -4
Jadi p+q=4+(-4)=0
6.
Perhatikan matriks dibawah ini!
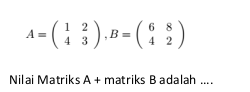
A.

B.

C.

D.

E.

JAWABAN BENAR
E.

PEMBAHASAN
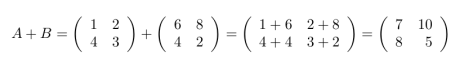
7.
Perhatikan matriks dibawah ini!

A.

B.

C.

D.

E.

JAWABAN BENAR
A.

PEMBAHASAN

Oops!!!
Yah, jawaban kamu meleset nih. Ingin melihat pembahasan soal ini?

BENAR!!!
Selamat!
Jawaban kamu benar. Ingin lihat pembahasan soal ini?
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved

