APSiswaNavbarV2

redesain-navbar Portlet

BelajarPintarV3

Matematika Wajib

Program Linear

Daftar Materi

MATERI

Membuat Model Matematika dari Masalah Program Linear


 

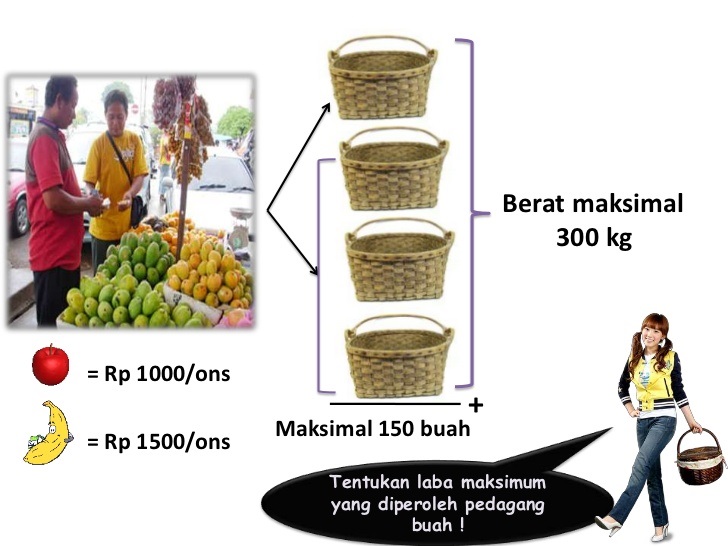
Sumber : pt.slideshare.net

Sobat, dalam kehidupan sehari-hari, setiap orang yang hendak mencapai tujuan pasti akan berhadapan dengan kendala-kendala yang berkaitan dengan tujuan tersebut. Masalah kontekstual dalam kehidupan sehari-hari dapat dinyatakan dengan model matematika untuk diselesaikan dengan program linear.

Masalah program linear dua variabel adalah menentukan nilai x,y yang mengoptimumkan (maksimum atau minimum) fungsi tujuan Z(x,y)=C1 x+C2 y dengan kendala:

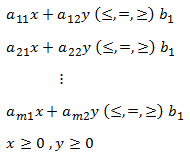
Langkah-langkah dalam membuat model matematika dari kendala yang ada yaitu :

  1. Tuliskan kendala pada soal dengan bantuan tabel
  2. Tentukan besaran masalah sebagai variabel yang akan digunakan
  3. Buatlah Sistem Pertidaksamaan Linear Dua Variabel berdasarkan kendala pada tabel
  4. Tentukan fungsi tujuan sebagai fungsi yang akan menjadi nilai optimum

Menentukan Nilai Optimum dari Fungsi Tujuan


 

Setelah membuat model matematika berdasarkan informasi yang tersedia pada soal, kita dapat menentukan nilai optimum suatu fungsi tujuan dengan menggambarkan grafik daerah penyelesaian. Daerah penyelesaian masalah program linear merupakan himpunan semua titik (x,y) yang memenuhi kendala suatu masalah program linear. Kemudian menentukan nilai optimumnya dengan metode uji titik sudut dan metode garis selidik.

Metode Uji Titik Sudut

Menentukan nilai optimum dari fungsi tujuan dengan metode uji titik sudut menggunakan langkah-langkah berikut:

  1. Setelah menggambar grafik daerah penyelesaian, tentukan koordinat titik sudut dari daerah penyelesaian.
  2. Hitung nilai fungsi tujuan pada masing-masing titik sudut
  3. Nilai optimum dapat terlihat dengan membandingkan nilai-nilai fungsi tujuan pada setiap titik sudut

Metode Garis Selidik

Menentukan nilai optimum dari fungsi tujuan dengan metode garis selidik menggunakan langkah-langkah berikut:

  1. Setelah menggambar grafik daerah penyelesaian, lukis garis selidik ax+by=k, dengan k dapat diperbesar maupun diperkecil dan selidiki nilainya pada masing-masing titik sudut.
  2. Nilai optimum dicari dengan membandingkan nilai-nilai pada langkah sebelumnya

1.

Jawablah soal berikut!

Sebuah adonan roti basah dibuat dengan 2 kg tepung dan 1 kg gula. Sedangkan sebuah adonan roti kering dibuat menggunakan 2 kg tepung dan 3 kg gula. Ibu memiliki persediaan tepung sebanyak 6 kg dan gula sebanyak 5 kg. Jika setiap satu adonan kue basah dapat memberikan untung Rp75.000,00 dan setiap adonan kue kering dapat memberikan untung Rp60.000,00. Maka tentukan model matematika sesuai dengan permasalahan tersebut!


A.
B.
C.
D.
E.

JAWABAN BENAR

A.

PEMBAHASAN

Misalkan:

x = adonan roti basah

y = adonan roti kering

Sehingga diperoleh model matematika sebagai berikut :

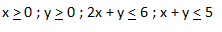
2.

Jawablah soal berikut!

Andi membeli 3 baju dan 5 celana dengan harga total Rp 350.000,-. Sedangkan Budi yang hanya membeli 1 baju dan 1 celana harus membayar Rp 90.000,-. Jika harga masing-masing sebuah baju dan sebuah celana adalah x dan y, buatlah model matematika untuk persoalan tersebut!


A.
B.
C.
D.
E.

JAWABAN BENAR

B.

PEMBAHASAN

Berdasarkan jumlah uang yang dibayarkan Andi diperoleh hubungan: 3x + 5y = 350.000

Berdasarkan jumlah uang yang dibayarkan Budi diperoleh hubungan: x + y = 90.000

Karena harga baju maupun celana tidak mungkin negatif ataupun gratis, maka x > 0 dan y > 0

Jadi, model matematikanya adalah: x > 0 , y > 0 , 3x + 5y = 350.000 dan x + y = 90.000

3.

Jawablah soal berikut!

Tentukanlah sebuah nilai minimum dari: f(x, y) = 9x + y pada daerah yang telah dibatasi oleh


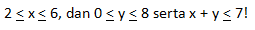
A. 17
B. 18
C. 19
D. 20
E. 21

JAWABAN BENAR

B.

18

PEMBAHASAN

  • Langkah pertama gambar grafiknya terlebih dahulu

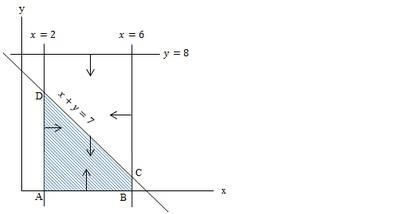
  • Langkah kedua menentukan titik-titik ekstrimnya:

Maka berdasarkan gambar di atas, ada 4 titik ekstrim, yaitu A, B, C, D dan himpunan penyelesaiannya ada di area yang telah diarsir

  • Langkah ketiga yaitu menyelidiki nilai optimum:

berdasarkan grafik di atas dapat diketahui titik A dan B mempunyai nilai y = 0 sehingga kemungkinan menjadi nilai minimum.

Kedua titik disubtitusikan ke dalam f(x,y) = 9x + y untuk dibandingkan

titik A(x,y) = A(2,0) disubtitusikan f(2,0) = 9(2) + 0 = 18

titik B(x,y) = B(6,0) disubtitusikan f(6,0) = 9(6) + 0 = 54

dengan membandingkan tersebut, maka disimpulkan bahwa titik A memiliki nilai minimum 18.

4.

Jawablah soal berikut!

Tentukanlah dimana nilai maksimum fungsi f(x, y) = 4x + 5y yang akan dicapai pada pada grafik ini!


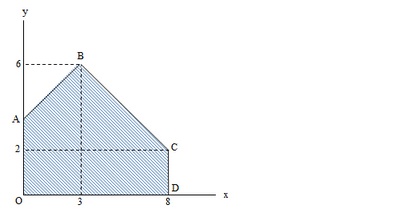
A. 32
B. 40
C. 41
D. 42
E. 46

JAWABAN BENAR

D.

42

PEMBAHASAN

Titik ekstrim pada gambar adalah :

  • A tidak mungkin maksimum karena titik A paling kiri
  • B(3,6)
  • C(8,2)
  • D(8,0)

Nilai tiap titik ekstrim adalah :

  • B(3,6) maka f(3,6) = 4(3) + 5(6) = 42
  • C(8,2) maka f(8,2) = 4(8) + 5(2) = 42
  • D(8,0) maka f(8,0) = 4(8) + 5(0) = 32

sehingga dapat diketahui hasilnya bahwa nilai maksimumnya berada pada titik yang melalui garis BC dengan nilai maksimum 42 

5.

Jawablah soal berikut!

Tanah seluas 9.000 m2 akan dibangun ruko sebanyak 2 tipe. Untuk tipe A diperlukan tanah seluas 100 m2 dan tipe B diperlukan 75 m2. Banyak ruko yang dibangun paling banyak 100 unit. Keuntungan tiap tipe A Rp15.000.000,00 dan tipe B sebesar Rp10.000.000,00. Keuntungan maksimum yang diperoleh jika membangun ruko sebanyak ….


A. 60 ruko A dan 40 ruko B
B. 75 ruko A dan 25 ruko B
C. 50 ruko A dan 50 ruko B
D. Hanya 100 ruko B
E. Hanya 90 ruko A

JAWABAN BENAR

E.

Hanya 90 ruko A

PEMBAHASAN

a = banyak unit tipe A

b = banyak unit tipe B

Diperoleh pertidaksamaan:

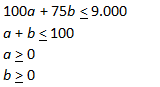
Fungsi Tujuan : f(a,b) = 15a + 10b (dalam jutaan)

Daerah Penyelesaian:

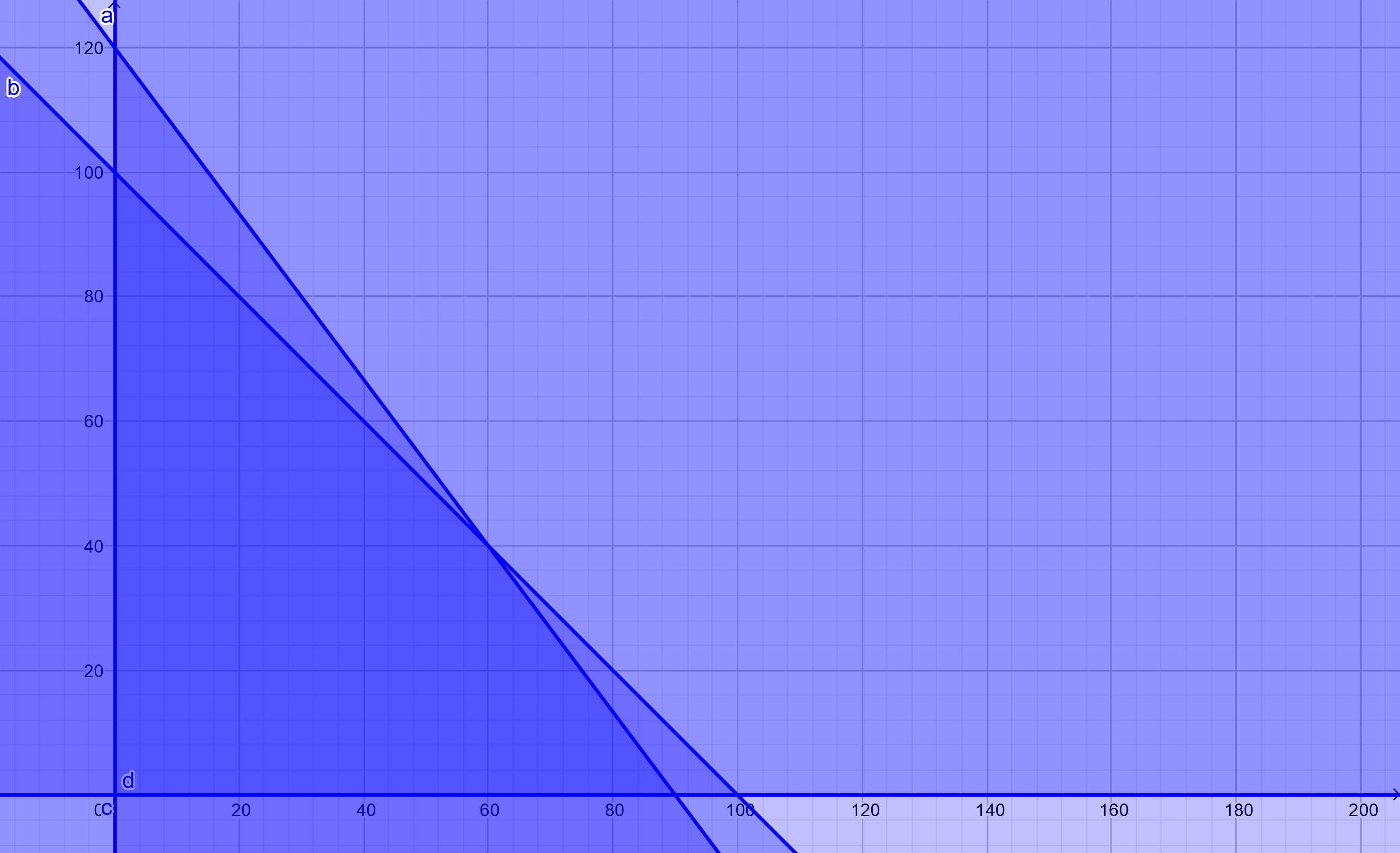
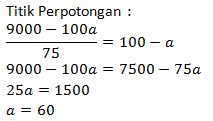
Sehingga diperoleh b = 40

Titik Penyelesaian : (90,0); (0,100), dan (60,40)

Fungsi Tujuan : f(a,b) = 15a + 10b (dalam jutaan)

f(90,0) = 15(90) + 10(0) = 1.350 (dalam jutaan)

f(0,100) = 15(0) + 10(100) = 1.000 (dalam jutaan)

f(60,40) = 15(60) + 10(40) = 1.300 (dalam jutaan) 

Keuntungan maksimum yang diperoleh 1.350 (dalam jutaan) jika membangun ruko sebanyak 90 ruko A.

6.

Jawablah soal berikut!

Seorang tukang jahit akan membuat pakaian model A dan model B. Model A memerlukan 1 m kain polos dan 1.5 m kain bergaris. Model B memerlukan 2 m kain polos dan 0.5 m kain bergaris. Persediaan kain polos 20 m dan bergaris 10 m. Banyaknya total pakaian jadi akan maksimal jika banyaknya model A dan model B masing-masing ....


A. 7 dan 8
B. 8 dan 6
C. 6 dan 4
D. 5 dan 9
E. 4 dan 8

JAWABAN BENAR

E.

4 dan 8

PEMBAHASAN



 

7.

Jawablah soal berikut!

Sebuah angkutan umum paling banyak dapat memuat 50 penumpang. Tarif untuk seorang pelajar dan mahasiswa berturut-turut adalah Rp1.500,- dan Rp2.500,-. Penghasilan yang diperoleh tidak kurang dari Rp75.000,-. Misal banyak penumpang pelajar dan mahasiswa masing-masing x dan y. Model matematika yang sesuai untuk permasalahan tersebut adalah ....


A.
B.
C.
D.
E.

JAWABAN BENAR

A.

PEMBAHASAN


 

redesain-navbar Portlet