Belajar Pintar Materi SMP, SMA, SMK
BelajarPintarV3
Matematika Wajib
Program Linear
MATERI
Pertidaksamaan Linear Dua Variabel

Sobat Pintar, suatu pertidaksamaan dikatakan sebagai pertidaksamaan linear dua variabel ketika pertidaksamaan tersebut memiliki dua variabel dengan masing-masing variabel berderajat satu.
Bentuk umum dari pertidaksamaan linear dua variabel yaitu :
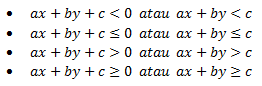
dengan keterangan :
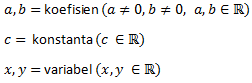
Pertidaksamaan linear dua variabel memiliki himpunan penyelesaian yang tak terhingga banyaknya. Himpunan penyelesaian pertidaksamaan linear dua variabel biasanya ditampilkan dalam bentuk grafik pada bidang cartesius.
Langkah-langkah dalam mencari himpunan penyelesaian suatu pertidaksamaan linear dua variabel dapat dilakukan dengan cara sebagai berikut
Membuat garis ax+by=c
- menentukan titik potong garis ax+by=c dengan sumbu-X (y=0) dan sumbu-Y (x=0) sehingga diperoleh dua titik yaitu (x,0) dan (0,y)
- menghubungkan dua titik tersebut menjadi sebuah garis
Menguji titik pada salah satu daerah di luar garis
-
pilih satu titik uji P(x1, y1) yang berada di luar garis ax+by=c
-
hitunglah nilai dari ax1 +by1
-
bandingkan nilai dari ax1 + by1 dengan nilai c, yaitu :
a. jika ax1 + by1 < c, maka bagian yang memuat titik P(x1, y1) menjadi daerah himpunan penyelesaian dari pertidaksamaan ax+by<c
b. jika ax1 + by1 >c, maka bagian yang memuat titik P(x1, y1) menjadi daerah himpunan penyelesaian dari pertidaksamaan ax+by>c
Sistem Pertidaksamaan Linear Dua Variabel

Sistem yang terbentuk dari dua atau lebih pertidaksamaan linear dua variabel dengan variabel yang sama disebut dengan sistem pertidaksamaan linear dua variabel atau biasa disingkat dengan SPtLDV. Daerah himpunan penyelesaian dari SPtLDV merupakan irisan dari masing-masing daerah himpunan pertidaksamaan linear yang membentuknya.
Salah satu contoh dari SPtLDV yaitu:
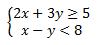
1.
Jawablah soal berikut ini!

A.

B.

C.

D.

E.

JAWABAN BENAR
A.

PEMBAHASAN
Daerah penyelesaiannya adalah

2.
Jawablah soal berikut ini!
Daerah penyelesaian sistem pertidaksamaan:
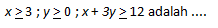
A.

B.

C.

D.

E.

JAWABAN BENAR
B.

PEMBAHASAN

3.
Jawablah soal berikut ini!
Daerah penyelesaian dari sistem persamaan linear di bawah ini adalah ....
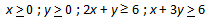
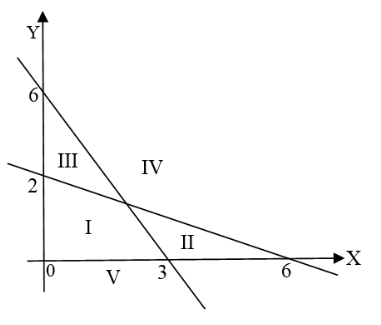
A. I
B. II
C. III
D. IV
E. V
JAWABAN BENAR
D.
IV
PEMBAHASAN
Titik potong garis 2x + y > 6 terhadap sumbu koordinat dapat dinyatakan (0,6) dan (3,0)
Daerah II dan IV adalah daerah penyelesaian untuk pertidaksamaan ini karena bertanda > (arsirannya ke atas).
Titik potong garis x + 3y > 6 terhadap sumbu koordinat dapat dinyatakan (0,2) dan (6,0)
Daerah III dan IV adalah daerah penyelesaian untuk pertidaksamaan ini karena bertanda > (arsirannya ke atas).
Perhatikan bahwa pertidaksamaan x > 0,y > 0 membatasi daerah penyelesaiannya hanya pada kuadran pertama. Daerah irisannya adalah daerah IV.
Jadi, daerah penyelesaian sistem pertidaksamaan linear tersebut adalah daerah IV.
4.
Jawablah soal berikut!
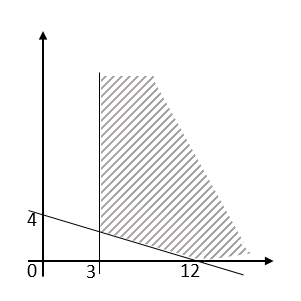
Perhatikan daerah penyelesaian sistem pertidaksamaan di bawah ini!
Daerah yang diarsir merupakan penyelesaian dari sistem pertidaksamaan ….
A.

B.

C.

D.

E.

JAWABAN BENAR
C.

PEMBAHASAN

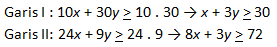
Karena di kuadran I sehingga dibatasi oleh x > 0 dan y > 0
Penyelesaian dari sistem pertidaksamaan tersebut adalah x + 3y > 30; 8x + 3y > 72; x > 0; y > 0
5.
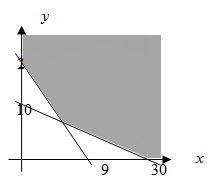
Perhatikan grafik berikut ini!
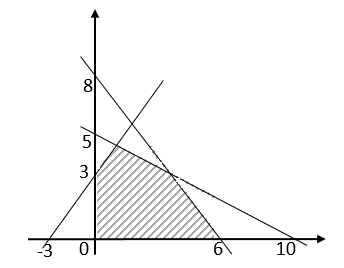
Sistem pertidaksamaan linear yang memenuhi dari daerah yang diarsir pada gambar di atas adalah ….
A. x > 0 ; y > 0 ; 5x + 10y > 50 ; 8x +6y > 48 ; 3y + 3x > 9
B.

C.

D.

E.

JAWABAN BENAR
D.

PEMBAHASAN
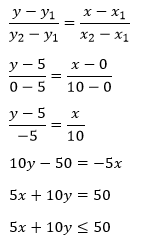
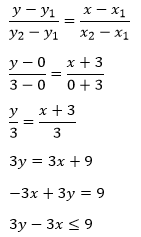
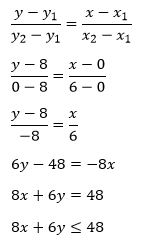
6.
Jawablah soal berikut!
Tentukanlah sistem pertidaksamaan untuk daerah yang diarsir pada gambar di bawah ini!
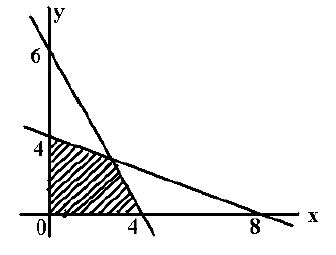
A.

B.

C.

D.

E.

JAWABAN BENAR
D.

PEMBAHASAN
Untuk menentukan sistem pertidaksamaan pada gambar di atas, harus ditentukan terlebih dahulu persamaan garis lurus yang menjadi batas-batas daerahnya, yakni dengan menggunakan rumus :


7.
Jawablah soal berikut!
Tentukanlah sistem pertidaksamaan untuk dearah yang diarsir pada gambar di bawah ini!
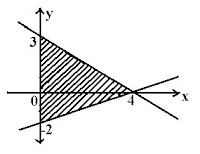
A.

B.

C.

D.

E.

JAWABAN BENAR
B.

PEMBAHASAN



Oops!!!
Yah, jawaban kamu meleset nih. Ingin melihat pembahasan soal ini?

BENAR!!!
Selamat!
Jawaban kamu benar. Ingin lihat pembahasan soal ini?
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved

