Belajar Pintar Materi SMP, SMA, SMK
BelajarPintarV3
Matematika Wajib
Turunan
MATERI
Konsep Kemonotonan Fungsi

Sumber : Jawapos.com
Selain kecepatan, banyak sekali aplikasi dari turunan suatu fungsi lho, Sobat Pintar!
Salah satunya adalah kita dapat menggambarkan kurva yang berbentuk gelombang seperti pada gambar di atas.
Aplikasi turunan yang pertama adalah kemonotonan fungsi, maksudnya kita dapat menentukan suatu fungsi naik atau turun pada suatu interval tertentu.
Konsep kemonotonan fungsi dapat didefinisikan:

Hubungannya dengan turunan suatu fungsi diperlihatkan pada teorema berikut:

Nilai Maksimum dan Minimum Fungsi
NILAI STASIONER DAN TITIK STASIONER
Titik stasioner pada kurva y = f(x) merupakan sebuah titik pada kurva dengan gradien dari garis singgung kurva bernilai 0 (nol). Jika fungsi f(x) kontinu dan diferensiabel maka f(a) dikatakan NILAI STASIONER dari f(x) jika dan hanya jika f’(a)=0. Titik stasioner disebut juga titik kritis atau titik ekstrem atau titik balik.
Jenis-jenis ekstrem suatu fungsi
Turunan Pertama Fungsi
Jenis-jenis nilai stasioner dapat ditentukan dengan memperhatikan tanda f’(x) di sekitar x = a
- Jika f’(a-) < 0 dan f’(a+) > 0, maka f(a) merupakan nilai balik minimum
- Jika f’(a-) > 0 dan f’(a+) < 0, maka f(a) merupakan nilai balik maksimum
- Jika f’(a-) dan f’(a+) bertanda sama, maka f(a) merupakan nilai belok horizontal
Keterangan:
f’(a-) merupakan nilai f’(x) untuk x kurang dari a
f’(a+) merupakan nilai f’(x) untuk x lebih dari a
Turunan Kedua Fungsi
Titik (a,f(a)) dikatakan titik belok dari f(x) jika:
- f’(a) = 0
- f’’(a)=0
Dalam menentukan jenis ekstrem fungsi dapat menggunakan uji turunan kedua, yaitu:
- Jika f’’(a) < 0 maka f(a) adalah nilai balik maksimum fungsi f
- Jika f’’(a) > 0 maka f(a) adalah nilai balik minimum fungsi f
- Jika f’’(a) = 0 maka f(a) bukan nilai ekstrem fungsi f
NILAI MAKSIMUM ATAU MINIMUM FUNGSI PADA INTERVAL TERTENTU
Nilai maksimum atau minimum suatu fungsi yang kontinus dan diferensiabel pada setiap titik di interval [a,b] dapat terjadi pada:
- Titik stasioner yang berada pada interval [a,b]
- Titik ujung interval
Dalam menentukan nilai maksimum atau minimum suatu fungsi dapat dilakukan langkah-langkah berikut:
- Menentukan titik stasioner pada fungsi f(x) yang berada pada interval [a,b].
- Menentukan nilai fungsi pada ujung interval, yaitu f(a) dan f(b).
- Membandingkan nilai fungsi pada langkah 1 dan 2. Nilai yang terbesar adalah nilai maksimum, sedangkan nilai terkecil adalah nilai minimum.
Menentukan Persamaan Garis Singgung Kurva

Persamaan garis lurus yang melalui titik P(x1,y1) dengan gradien m, yaitu :
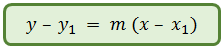
Gradien suatu fungsi yang melalui titik A (a,f(a)) dapat ditentukan dengan m = f’(a)
Jadi, PGS di titik A (a,f(a)) pada kurva adalah
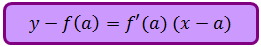
Permasalahan dalam Kehidupan Nyata

MENENTUKAN KECEPATAN DAN PERCEPATAN
Jika diketahui sebuah benda bergerak menempuh jarak s = f(t), maka kecepatan dan percepatan benda tersebut dapat dirumuskan sebagai berikut:
Kecepatan benda saat t detik (turunan pertama)
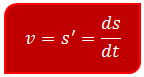
Percepatan benda saat t detik (turunan kedua)
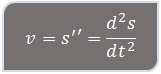
MENENTUKAN LAJU PERUBAHAN NILAI FUNGSI TERHADAP VARIABEL BEBASNYA
Perubahan banyaknya suatu variabel bebas biasanya dinyatakan dengan sebuah fungsi, untuk menentukan laju perubahannya dapat menggunakan definisi dari turunan fungsi.
Misalkan banyaknya populasi dari makhluk hidup setelah t tahun dinyatakan dengan fungsi f(t), maka laju perkembangan populasi setelah a tahun dapat dinyatakan dengan:
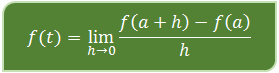
MENENTUKAN LAJU PERTAMBAHAN NILAI FUNGSI
Laju perubahan nilai fungsi y = f(x) terhadap x dapat dinyatakan dalam bentuk:
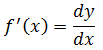
Berdasarkan aturan rantai, diketahui bahwa:
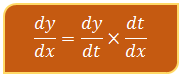
Rumus tersebut digunakan untuk menentukan laju pertambahan nilai fungsi y = f(x) seiring pertambahan variabel x terhadap variabel t saat nilai x ditetapkan.
1.
Jawablah soal berikut!
Persamaan garis singgung kurva y=3x2 + 5x - 3 di titik(-2,7) adalah ....
A. y = 6x + 5
B. y = -7x + 2
C. y = 7x - 14
D. y = -7x - 7
E. y = 7x + 7
JAWABAN BENAR
D.
y = -7x - 7
PEMBAHASAN
y=3x2 + 5x - 3
y'=6x + 5
f'(-2)=6.(-2) + 5
f'(-2)= -12 + 5= -7
Gradien garis singgung = m = f'(-2) = -7
Persamaan garis singgungnya:
y - y1 = m (x - x1)
y - 7= -7 (x - (-2))
y - 7 = -7x - 14
y = -7x - 14 + 7
y = -7x - 7
2.
Jawablah soal berikut!
Persamaan garis singgung dari kurva f(x) = 5x2 - 3x yang sejajar dengan garis y = 7x - 1 adalah ....
A. 7x - 5
B. 10x - 3
C. 5x - 3
D. 7x - 7
E. 7x - 1
JAWABAN BENAR
A.
7x - 5
PEMBAHASAN
Gradien garis y=7x-1 adalah 7
Karena kurva sejajar dengan garis y=7x-1, maka m1=m2=7
f(x)=5x2-3x
f'(x)=10x-3
7=10x-3
7+3=10x
10=10x
x=10/10=1
f(1)=5.12-3.1
f(1)=5-3=2
Maka persamaan garis singgung yang sejajar dengan garis y = 7x - 1 pada kurva f(x) = 5x2 - 3x, yaitu:
y-y1=m(x-x1 )
y-2=7(x-1)
y-2=7x-7
y=7x-7+2
y=7x-5
3.
Jawablah soal di bawah ini!
Titik stasioner dari fungsi f(x) = x3 - 3x2 + 3x - 2 adalah ....
A. (1, 1)
B. (-1, 1)
C. (1, -1)
D. (-1, -1)
E. (1, 0)
JAWABAN BENAR
C.
(1, -1)
PEMBAHASAN
f(x) = x3 - 3x2 + 3x - 2
f'(x) = 3x2 - 6x + 3
Titik stasioner ada jika f'(x)=0
0= 3x2 - 6x + 3
0=3 (x2-2x+1)
0=3 (x-1)2
x=1
f(1) = 13 - 3.12 + 3.1 - 2
f(1) = 1-3+3-2 = -1
Titik stasioner = (x,f(x)) = (1,-1)
4.
Jawablah soal di bawah ini dengan tepat!
Interval turun dari fungsi x3 - 12x - 5 adalah ....
A. x > 2
B. -2 < x < 2
C. x < -2
D. x < -2 atau x > 2
E. x > 0
JAWABAN BENAR
B.
-2 < x < 2
PEMBAHASAN
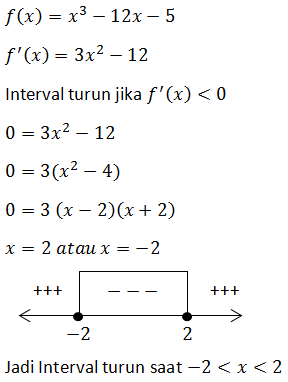
5.
Jawablah soal berikut dengan tepat!
Sebuah bola menggelinding pada sebuah lintasan. Panjang lintasan didefinisikan dengan persamaan s=7-3t2+t3 dengan t sebagai waktu yang ditempuh. Kecepatan sesaat bola saat detik ke-2 yaitu ....
A. 0 m/s
B. 1 m/s
C. 2 m/s
D. 3 m/s
E. 4 m/s
JAWABAN BENAR
A.
0 m/s
PEMBAHASAN
s = 7 - 3t2 + t3
v = s' = -6t + 3t2
Jika t=2 , maka
v = -6.2 + 3.22
v = -12 + 12
v = 0
6.
Jawablah soal berikut dengan tepat!
Suatu perusahaan memproduksi x unit barang dengan biaya 4x2 - 8x + 24 ribu rupiah untuk tiap unit. Jika barang tersebut terjual habis dengan harga Rp 40.000,00 untuk tiap unit, maka keuntungan maksimum yang diperoleh perusahaan tersebut adalah ....
A. Rp 16.000,00
B. Rp 32.000,00
C. Rp 48.000,00
D. Rp 52.000,00
E. Rp 64.000,00
JAWABAN BENAR
B.
Rp 32.000,00
PEMBAHASAN

7.
Jawablah soal berikut dengan tepat!

A. 80
B. 100
C. 150
D. 240
E. 320
JAWABAN BENAR
C.
150
PEMBAHASAN


Oops!!!
Yah, jawaban kamu meleset nih. Ingin melihat pembahasan soal ini?

BENAR!!!
Selamat!
Jawaban kamu benar. Ingin lihat pembahasan soal ini?
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved

