Belajar Pintar Materi SMP, SMA, SMK
BelajarPintarV3
Fisika
Vektor
Daftar Materi
MATERI
Penjumlahan dan Pengurangan Vektor dengan Metode Grafis

Halo Sobat Pintar, Operasi vektor terdiri dari penjumlahan, pengurangan, dan perkalian vektor. Hasil dari penjumlahan atau pengurangan vektor disebut sebagai resultan vektor.
Penjumlahan dua vektor dapat dilakukan dengan menghubungkan ujung vektor pertama dengan pangkal vektor kedua. Resultan vektor diperoleh dengan menarik anak panah dari pangkal vektor pertama ke ujung vektor kedua.
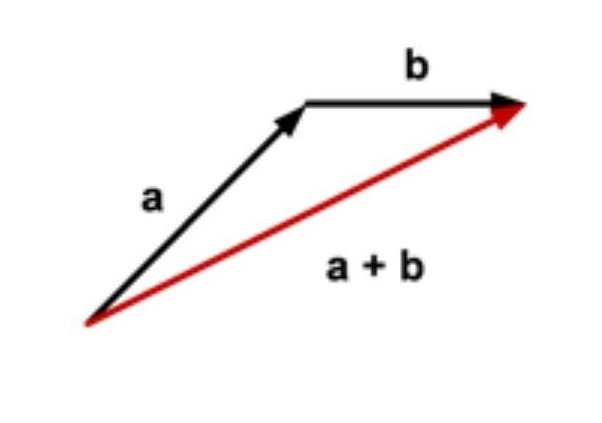
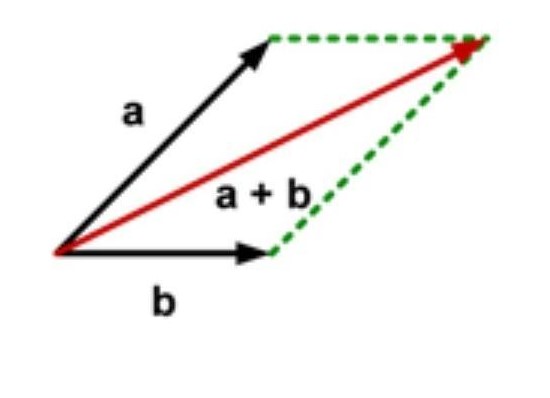
Metode jajargenjang juga bisa digunakan untuk penjumlahan dua vektor, yaitu dengan mempertemukan kedua pangkal vektor pada suatu titik dan menarik anak panah dari titik tersebut ke perpotongan proyeksi masing-masing vektor. Gambar menunjukkan cara mendapatkan resultan vektor dengan metode jajargenjang.
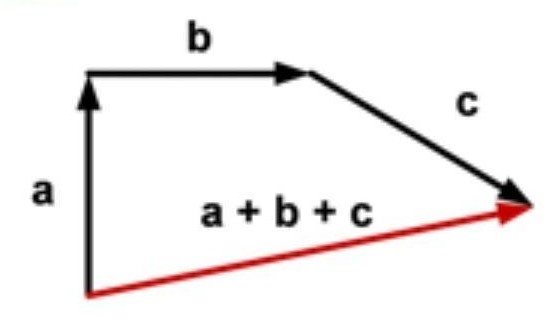
Jika lebih dari dua vektor dijumlahkan, resultan vektor dapat ditemukan dengan menggunakan metode poligon, dengan prinsip yang sama seperti metode segitiga.
Vektor nol terjadi dalam dua situasi:
- Ketika dua vektor senilai tetapi berlawanan arah, hasil penjumlahan keduanya adalah vektor nol.
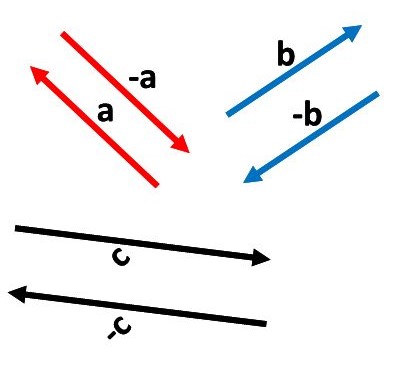
- Penjumlahan vektor B, vektor D, dan vektor C juga menghasilkan vektor nol. Hasil penjumlahan vektor B dan C merupakan vektor negatif dari vektor D.
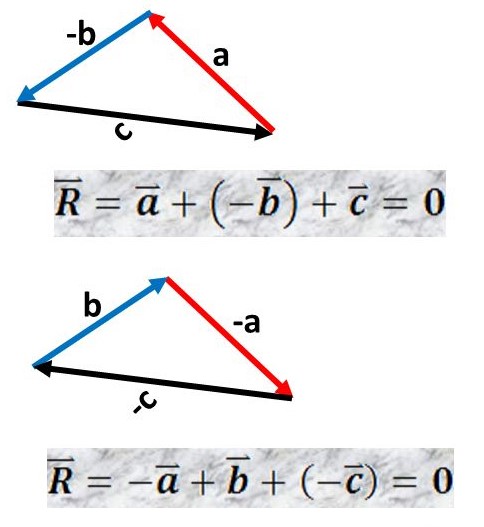
"Vektor nol adalah vektor yang pangkal dan ujungnya berhimpit. Vektor nol memiliki panjang nol dan arahnya tidak tentu."
Penjumlahan dan Pengurangan Vektor dengan Metode Analitis

Sobat Pintar, berbeda dengan metode sebelumnya yang memerlukan penggaris dan busur untuk menentukan resultan vektor, metode analitis membutuhkan penguasaan trigonometri untuk menyelesaikannya.
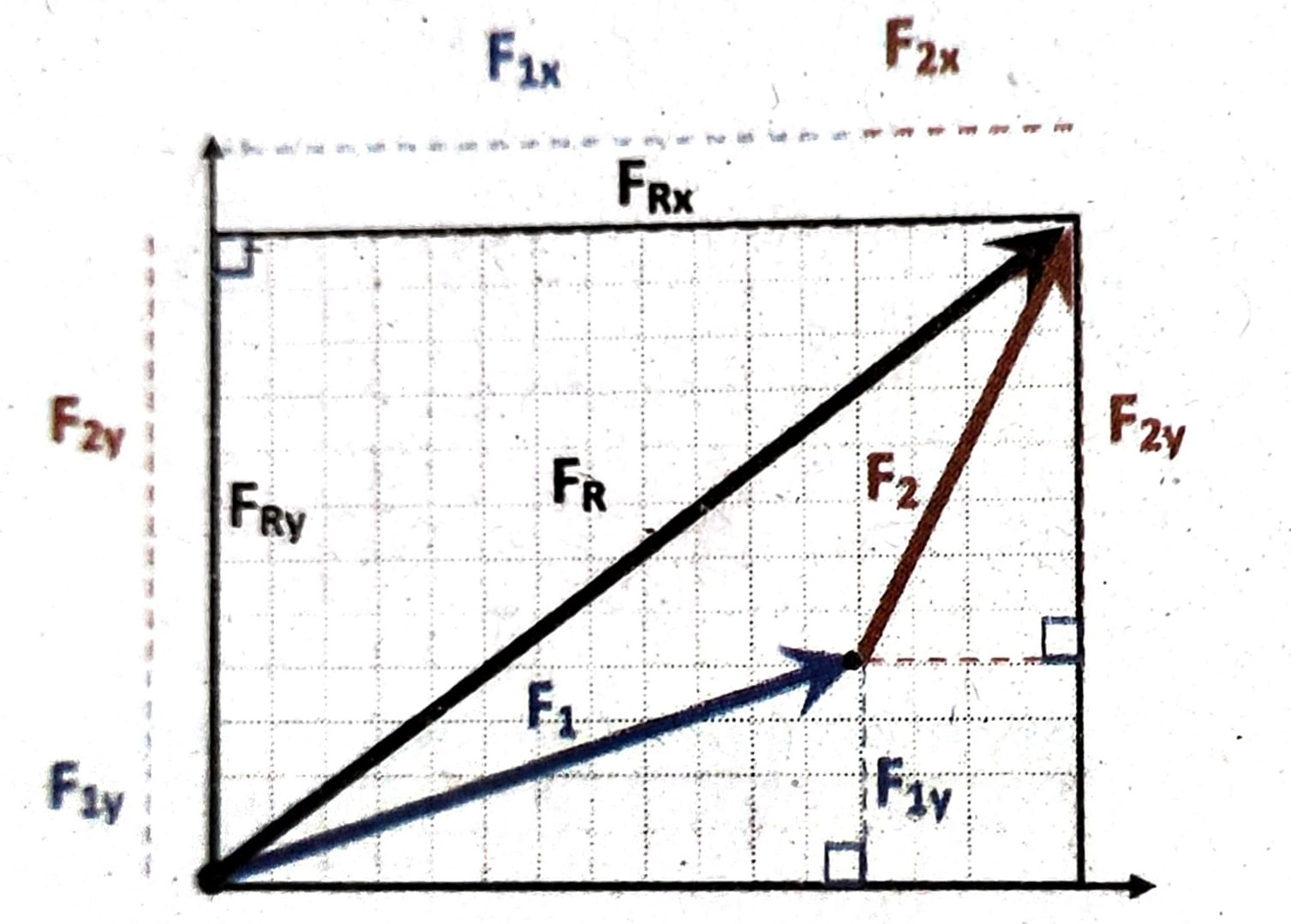
Besar setiap komponen vektor pada sumbu x dan pada sumbu diberikan oleh
Fx = F cos a dan Fy = F sin a
Besar resultan vektor pada sumbu x dan sumbu y adalah:
FRx = sigma Fx = F1x + F2x
FRy = sigma Fy = F1y + F2y
Besar dan arah resultan vektor adalah:
FR = akar (F2Rx + F2Ry) dan tan a = Fy/Fx
Jika terdapat lebih dari dua vektor maka besar resultan vektor pada sumbu x dan sumbu y adalah:
FRx = sigma Fx = F1x + F2x + F3x + ....
FRy = sigma Fy = F1y + F2y + F3y + ....
Penentuan Resultan Vektor dengan Menggunakan Rumus Kosinus

Sobat Pintar, besarnya resultan dari dua buah vektor F1 dan F2 yang membentuk sudut apit alpha dapat dihitung dengan persamaan kosinus berikut
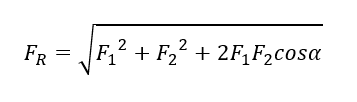
dengan
FR = besar resultan dari dua vektor
F1 = besar vektor pertama
F2 = besar vektor kedua
alpha = sudut apit antara kedua vektor
Penentuan Resultan Vektor dengan Menggunakan Rumus Sinus

Jika menggunakan rumus kosinus untuk mendapatkan besar resultan dari penjumlahan dua vektor, Sobat juga dapat menggunakan persamaan sinus untuk menentukan arah dari vektor resultan terhadap salah satu vektor komponennya.
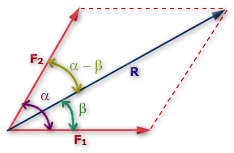
Misalkan sudut antara vektor F1 dan F2 adalah alpha. Sudut antara vektor resultan (R) dengan vektor F1 adalah beta, sedangkan sudut antara resultan (R) dan vektor F2 adalah alpha - beta. Secara matematis, persamaan ini dapat ditulis sebagai berikut
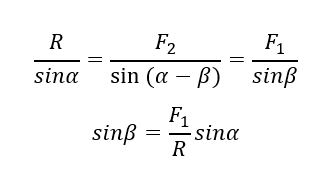
Perkalian Vektor

Sobat Pintar, dalam dunia vektor, terdapat dua jenis perkalian vektor yaitu perkalian titik (dot product) dan perkalian silang (cross product).
Ketika Sobat mendorong pensil pada pusat massa, kalian memberikan usaha pada pensil. Semakin besar gaya yang diberikan dan perpindahan yang dialami oleh pensil, maka semakin besar usaha yang diterima oleh pensil. Usaha dihitung sebagai hasil perkalian antara gaya dan perpindahan.
Mendorong ujung pensil menyebabkan pensil berputar. Arah putaran bergantung pada arah dorongan. Penempatan jari pada pensil juga memengaruhi putaran, dimana semakin jauh dari sumbu putar, putarannya menjadi lebih mudah. Torsi atau momen gaya bekerja pada pensil sehingga pensil yang awalnya diam menjadi berputar.
Perbedaan di antara usaha dan momen gaya adalah dalam hal vektor yang terlibat. Usaha melibatkan perkalian dua vektor yang menghasilkan skalar, disebut sebagai dot product. Sementara itu, momen gaya melibatkan perkalian dua vektor yang menghasilkan vektor, disebut sebagai cross product. Momen gaya adalah vektor karena arahnya dapat berupa searah atau berlawanan dengan arah jarum jam.
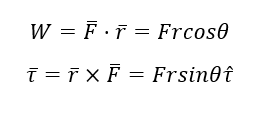
1.
Sobat Pintar, yuk kerjakan soal di bawah ini dengan benar!
Terdapat dua buah gaya saling tegak lurus, besarnya masing-masing 12 N dan 16 N.Berapakah besar resultan kedua gaya tersebut?
A. 5 N
B. 10 N
C. 15 N
D. 20 N
E. 25 N
JAWABAN BENAR
D.
20 N
PEMBAHASAN
Hanya terdapat dua vektor dan kedua vektor saling tegak lurus sehingga penyelesaiannya menggunakan rumus Pythagoras.
FR2 = F12 + F22
FR2 = 122 + 162
FR2 = 20 N
2.
Sobat Pintar, yuk kerjakan soal di bawah ini dengan benar!
Besar dan arah vektor A= 8i + 8j adalah ....
A. 8 satuan pada 45o
B. 8 akar 2 satuan pada 45o
C. 16 satuan pada 45o
D. 18 satuan pada 45o
E. 64 satuan pada 45o
JAWABAN BENAR
B.
8 akar 2 satuan pada 45o
PEMBAHASAN
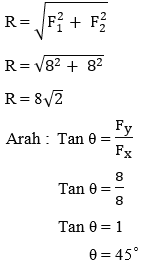
3.
Sobat Pintar, yuk kerjakan soal di bawah ini dengan benar!
Dua buah vektor satu sama lain membentuk sudut 60o. Besar kedua vektor tersebut sama, yakni 5 satuan. Tentukanlah resultan nya!
A.
![]()
B.
![]()
C.
![]()
D.
![]()
E.
![]()
JAWABAN BENAR
C.
![]()
PEMBAHASAN

4.
Sobat Pintar, yuk kerjakan soal di bawah ini dengan benar!
Dua buah vektor satu sama lain membentuk sudut 60o. Besar kedua vektor tersebut sama, yakni 5 satuan. Tentukanlah selisih nya!
A. 5 satuan
B. 7 satuan
C. 8 satuan
D. 9 satuan
E. 10 satuan
JAWABAN BENAR
A.
5 satuan
PEMBAHASAN
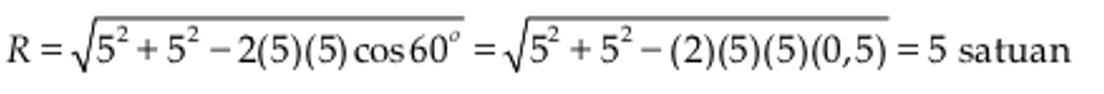
5.
Sobat Pintar, yuk kerjakan soal di bawah ini dengan benar!
Tiga orang siswa sedang menarik balok dengan gaya masing-masing sebagai berikut!
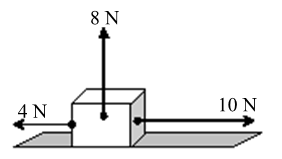
Berapakah resultan gaya pada balok tersebut?
A. 6 N
B. 10 N
C. 14 N
D. 18 N
E. 22 N
JAWABAN BENAR
B.
10 N
PEMBAHASAN
Fx = 10 N- 4N = 6 N ke arah kanan
Fy = 8 N
Karena tegak lurus sehingga untuk menentukan resultan gaya nya, kita menggunakan Phytagoras
C2 = A2 + B2
R2 = 62 + 82
R = 10 N

Oops!!!
Yah, jawaban kamu meleset nih. Ingin melihat pembahasan soal ini?

BENAR!!!
Selamat!
Jawaban kamu benar. Ingin lihat pembahasan soal ini?
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved

