APSiswaNavbarV2

redesain-navbar Portlet

BelajarPintarV3

Matematika Minat

Identitas Trigonometri

Daftar Materi

MATERI

Materi Prasyarat


Sobat pintar tidak perlu khawatir jika lupa dengan nilai perbandingan trigonometri pada sudut istimewa, karena kakak sudah siapkan tabel nilainya sebagai berikut.


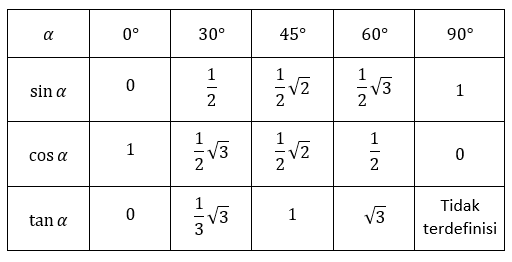
Selain nilai perbandingan trigonometri di atas, sobat pintar juga harus ingat perbandingan trigonometri di berbagai kuadran. Sekali lagi, sobat pintar tidak perlu risau karena kakak sudah siapkan.

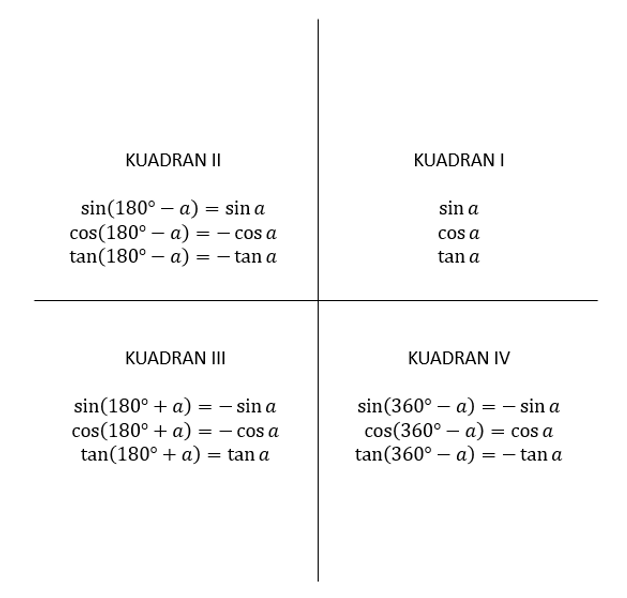
Persamaan Trigonometri Dasar


Sobat Pintar pasti sudah mengetahui tentang trigonometri, bukan?

Nah kali ini kita akan belajar tentang PERSAMAAN TRIGONOMETRI.

Perbedaan antara persamaan trigonometri dengan persamaan yang lain adalah persamaan trigonometri mengandung fungsi trigonometri dari suatu sudut yang belum diketahui nilainya.

Dalam menyelesaikan persamaan trigonometri bervariabel x, kita akan mencari nilai dari sudut x sehingga persamaan tersebut bernilai benar untuk suatu daerah tertentu, biasanya daerahnya dibatasi untuk satu putaran 

Tidak perlu lama-lama, bentuk persamaan trigonometri dasar ada 3, yaitu:

PERSAMAAN SINUS

Secara umum, bentuk persamaan trigonometri fungsi sinus, yaitu:

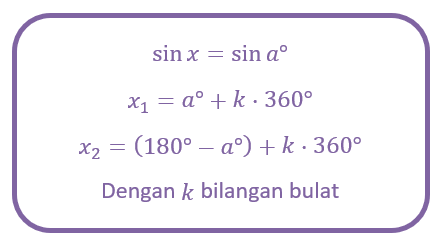
Dalam bentuk radian (pi) persamaan fungsi sinus adalah sebagai berikut.


 

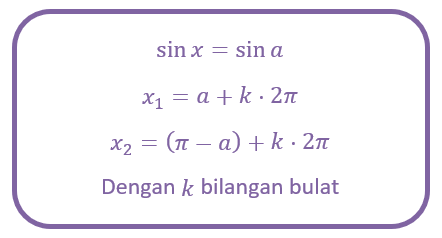
PERSAMAAN COSINUS

Sedangkan, bentuk umum persamaan trigonometri fungsi cosinus adalah:

Dalam bentuk radian (pi) persamaan fungsi cosinus adalah sebagai berikut.


 

PERSAMAAN TANGEN

Terakhir, bentuk umum persamaan trigonometri fungsi tangen adalah:

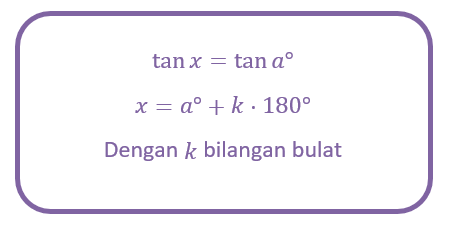
Dalam bentuk radian (pi) persamaan fungsi tangen adalah sebagai berikut.

 

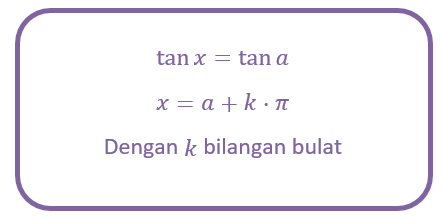
Sebagian sobat pintar mungkin ada yang bingung dengan maksud dari rumus-rumus persamaan trigonometri tadi, untuk memperjelas, sobat pintar bisa perhatikan contoh soal berikut.

Tentukan himpunan penyelesaian dari persamaan trigonometri berikut!

Pembahasan:



Persamaan Trigonometri Bentuk Lain


Persamaan trigonometri tidak selamanya akan berbentuk seperti bentuk umum yang telah sobat pintar pelajari. Untuk itu sobat pintar perlu rumus bantuan untuk bisa menyelesaikan persamaan tersebut.

Misal sobat pintar bertemu dengan persamaan m cos x + n sin x = c, maka sobat pintar bisa menggunakan rumus berikut untuk mengubahnya menjadi seperti bentuk umum, berikut rumusnya

Selain bentuk barusan, terdapat juga bentuk persamaan kuadrat trigonometri yang dapat diselesaikan dengan memfaktorkan persamaan tersebut untuk mencari penyelesaiannya. Misal persamaan kuadrat trigonometri yang mengandung sin x seperti berikut.

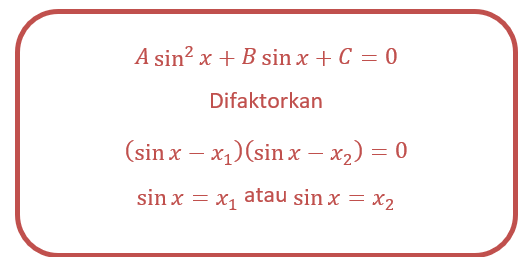
1.

Jawablah soal berikut!


A. {30°, 90°, 180°, 360°}
B. {45°, 90°, 180°, 270°}
C. {45°, 90°, 225°, 270°}
D. {30°, 45°, 60°, 90°}
E. {30°, 180°, 225°, 270°}

JAWABAN BENAR

C.

{45°, 90°, 225°, 270°}

PEMBAHASAN

Menyederhanakan persamaan

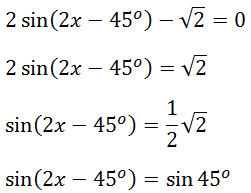
Substitusikan pada bentuk umum penyelesaian persamaan trigonometri fungsi sinus

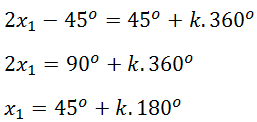
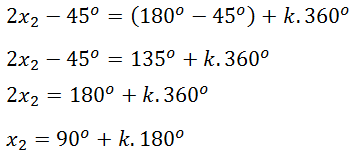
Jika k = 0, diperoleh:

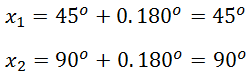
Jika k = 1, diperoleh:

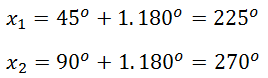
Untuk nilai k = 2 dan seterusnya akan menghasilkan nilai x yang lebih dari 360°, sehingga perhitungan cukup sampai k = 1.

Jadi, himpunan penyelesaian yang diperoleh adalah {45°, 90°, 225°, 270°}

2.

Jawablah soal berikut!


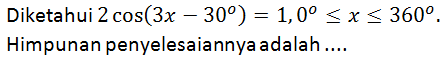
A. {30°, 110°, 150°, 230°, 270°}
B. {10°, 30°, 110°, 150°, 230°, 270°}
C. {10°, 30°, 150°, 225°, 270°}
D. {30°, 120°, 160°, 200°, 240°}
E. {30°, 60°, 90°, 180°, 270°}

JAWABAN BENAR

A.

{30°, 110°, 150°, 230°, 270°}

PEMBAHASAN

Menyederhanakan persamaan

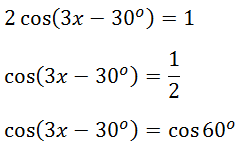
Substitusikan pada bentuk umum penyelesaian persamaan trigonometri fungsi cosinus

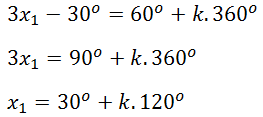
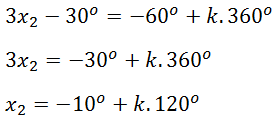
Jika k = 0, diperoleh:

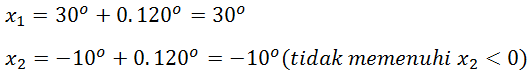
Jika k = 1, diperoleh:

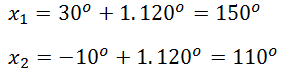
Jika k = 2, diperoleh:

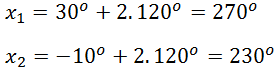
Untuk nilai k = 3 dan seterusnya akan menghasilkan nilai x yang lebih dari 360°, sehingga perhitungan cukup sampai k = 2.

Jadi, himpunan penyelesaian yang diperoleh adalah {30°, 110°, 150°, 230°, 270°}

3.

Jawablah soal berikut!


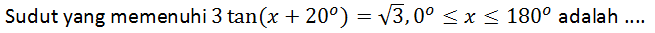
A. 0°
B. 10°
C. 15°
D. 30°
E. 45°

JAWABAN BENAR

B.

10°

PEMBAHASAN

Menyederhanakan persamaan

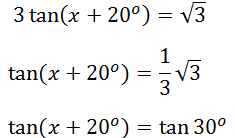
Substitusikan pada bentuk umum penyelesaian persamaan trigonometri fungsi tangen

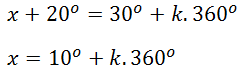
Jika k = 0, diperoleh:

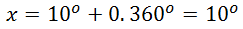
Untuk nilai k=1 dan seterusnya akan menghasilkan nilai x yang lebih dari 180°, sehingga perhitungan cukup sampai k=0.

Jadi, himpunan penyelesaian yang diperoleh adalah {10°}

4.

Jawablah soal berikut!


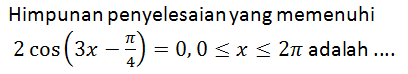
A.
B.
C.
D.
E.

JAWABAN BENAR

D.

PEMBAHASAN

Menyederhanakan persamaan

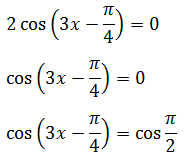
Substitusikan pada bentuk umum penyelesaian persamaan trigonometri fungsi cosinus

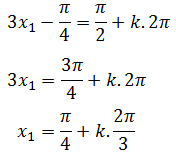
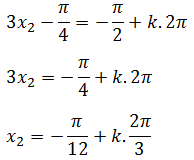
Jika k = 0, diperoleh:

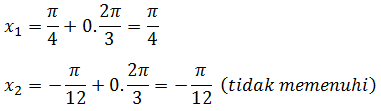
Jika k = 1, diperoleh:

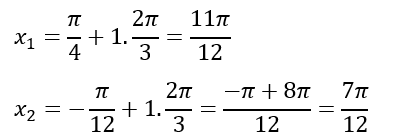
Jika k = 2, diperoleh:

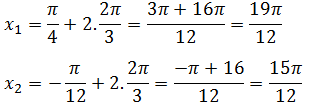
Untuk nilai k=3 dan seterusnya akan menghasilkan nilai x yang lebih dari

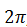
sehingga perhitungan cukup sampai k=2.

Jadi, himpunan penyelesaian yang diperoleh adalah

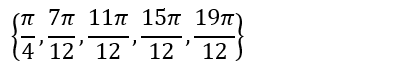
5.

Jawablah soal berikut!


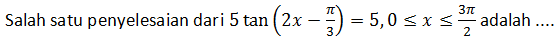
A.
B.
C.
D.
E.

JAWABAN BENAR

E.

PEMBAHASAN

Menyederhanakan persamaan

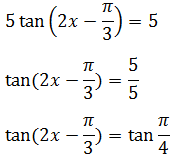
Substitusikan pada bentuk umum penyelesaian persamaan trigonometri fungsi tangen

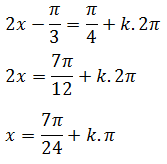
Untuk nilai k=2 dan seterusnya akan menghasilkan nilai x yang lebih dari

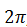
sehingga perhitungan cukup sampai k=1.

6.

Kerjakan soal berikut dengan tepat!


A.
B.
C.
D.
E.

JAWABAN BENAR

C.

PEMBAHASAN

7.

Kerjakan soal berikut dengan tepat!


A. {50°, 307°}
B. {106°, 254°}
C. {113°, 353°}
D. {148°, 219°}
E. {166°, 201°}

JAWABAN BENAR

C.

{113°, 353°}

PEMBAHASAN


redesain-navbar Portlet