Belajar Pintar Materi SMP, SMA, SMK
BelajarPintarV3
Matematika Minat
Limit Fungsi Trigonometri
MATERI
Pengertian Limit di Ketakhinggaan

Kita telah mempelajari limit fungsi untuk suatu nilai yang mendekati bilangan real tertentu, bagaimana jika suatu fungsi didekati dengan tak hingga bilangan?
Nah! Materi kali ini akan membahas mengenai konsep limit di ketakhinggaan.
Suatu limit dikatakan mendekati tak hingga jika dan hanya jika

Catatan:
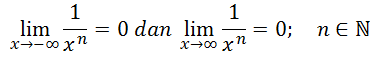
Menentukan Nilai Limit di Ketakhinggan Fungsi Aljabar

Fungsi aljabar yang nilainya dicari menggunakan limit di ketakhinggaan berupa:
- fungsi rasional bentuk pecahan
- fungsi irasional
LIMIT DI KETAKHINGGAAN FUNGSI RASIONAL PECAHAN
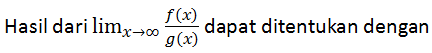
membagi f(x) dan g(x) dengan variabel berpangkat tertinggi yang terdapat pada f(x) maupun g(x).
Beberapa kemungkinan hasil yang diperoleh, antara lain:
- Jika variabel berpangkat tertinggi dari f(x) dan g(x) sama, maka:
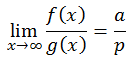
a = koefisien dari variabel berpangkat tertinggi f(x)
p = koefisien dari variabel berpangkat tertinggi g(x)
- Jika variabel berpangkat tertinggi f(x) lebih besar dari variabel berpangkat tertinggi g(x) dan koefisien dari variabel berpangkat tertinggi f(x) bernilai positif, maka:
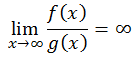
- Jika variabel berpangkat tertinggi f(x) lebih besar dari variabel berpangkat tertinggi g(x) dan koefisien dari variabel berpangkat tertinggi f(x) bernilai negatif, maka:
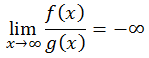
- Jika variabel berpangkat tertinggi f(x) lebih kecil dari variabel berpangkat tertinggi g(x), maka:

LIMIT DI KETAKHINGGAAN FUNGSI IRASIONAL

dapat ditentukan dengan mengalikan bentuk sekawannya.
- Jika diketahui fungsi Linear
Diketahui f(x)=ax+b dan g(x)=px+q, maka berlaku:
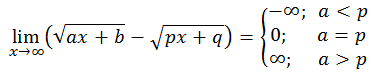
- Jika diketahui fungsi Kuadrat
Diketahui f(x)=ax2+bx+c dan g(x)=px2+qx+r, maka berlaku:
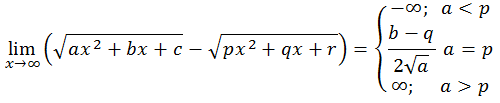
Menentukan Nilai Limit di Ketakhinggan Fungsi Trigonometri

Nilai limit di ketakhinggan fungsi trigonometri dapat diselesaikan menggunakan sifat-sifat yang berlaku pada limit fungsi geometri.

Contoh:

Aplikasi Limit Fungsi di Ketakhinggan Fungsi Trigonometri

Bagaimana cara menyelesaikan masalah yang berhubungan dengan konsep limit fungsi di ketakhinggan fungsi trigonometri?
Untuk memahaminya, ayo sobat pelajari contoh berikut!

ASIMTOT DATAR
Asimtot adalah suatu garis lurus yang didekati oleh lengkungan dengan jarak semakin lama semakin kecil mendekati nol di takhingga.
Asimtot juga diartikan sebagai garis batas atau garis arah kelengkungan kurva dan ada pada domain tertentu.
Jadi, asimtot datar adalah suatu garis yang mendekati nilai y tertentu tidak melewati atau menyinggungnya.

Untuk memahami tentang asimtot datar, ayo pelajari contoh berikut ini

1.
Jawablah soal berikut!
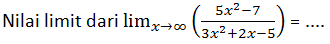
A. 1/3
B. 2/3
C. 1
D. 4/3
E. 5/3
JAWABAN BENAR
E.
5/3
PEMBAHASAN
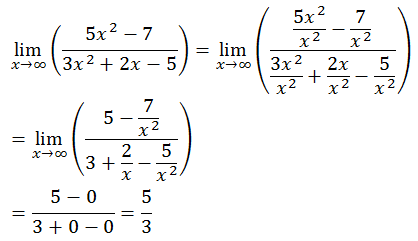
2.
Jawablah soal berikut!

A. 2
B. 1
C. 0
D. -1
E. -2
JAWABAN BENAR
C.
0
PEMBAHASAN
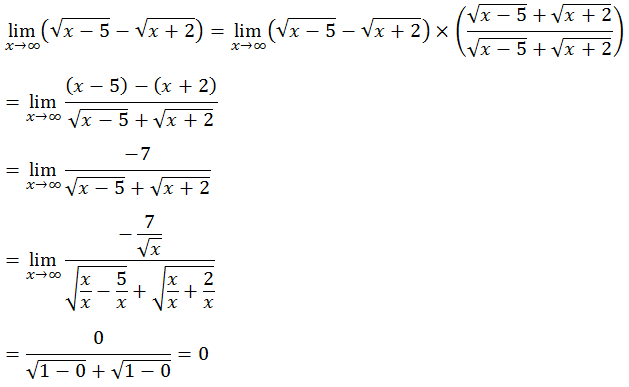
3.
Jawablah soal berikut!
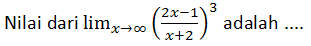
A. 16
B. 8
C. 4
D. 2
E. 1
JAWABAN BENAR
B.
8
PEMBAHASAN
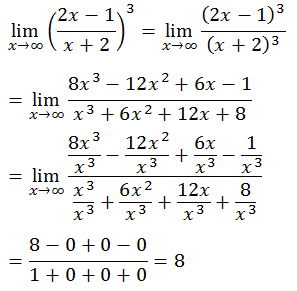
4.
Jawablah soal berikut!
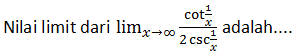
A. ~
B. 2
C. 1
D. 1/2
E. 0
JAWABAN BENAR
D.
1/2
PEMBAHASAN
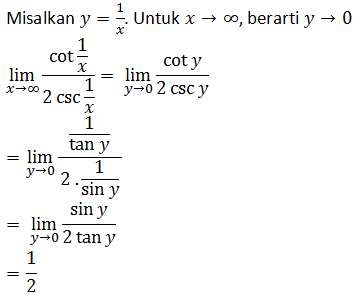
5.
Jawablah soal berikut!
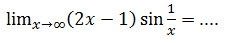
A. 2
B. 1
C. 0
D. -1
E. -2
JAWABAN BENAR
A.
2
PEMBAHASAN
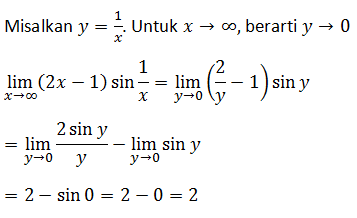
6.
Jawablah soal berikut!
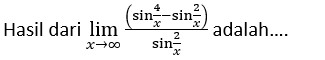
A. 0
B. 1
C. 2
D. 4
E. 8
JAWABAN BENAR
B.
1
PEMBAHASAN
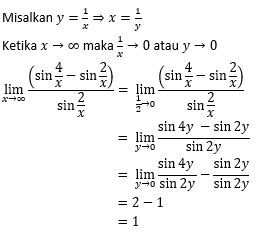
7.
Jawablah soal berikut!

A. -1
B. 0
C. 1
D. 2
E. 3
JAWABAN BENAR
C.
1
PEMBAHASAN


Oops!!!
Yah, jawaban kamu meleset nih. Ingin melihat pembahasan soal ini?

BENAR!!!
Selamat!
Jawaban kamu benar. Ingin lihat pembahasan soal ini?
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved

