Belajar Pintar Materi SMP, SMA, SMK
BelajarPintarV3
Matematika Wajib
Kaidah Pencacahan
MATERI
Kaidah Penjumlahan dan Perkalian


Sumber : Dekoruma.com
Sobat Pintar, pasti pernah bingung ketika memilih pakaian, kan? Wah, sama dong! hihihi...
Materi yang akan kita pelajari kali ini akan berhubungan dengan pilih memilih nih. Yuk, kita belajar bersama tentang permutasi dan kombinasi.
Sebelum kita belajar teori permutasi dan kombinasi, kita perlu memahami dulu tentang kaidah penjumlahan dan perkalian. Eitsss, tapi sebelum itu kalian harus paham dulu tentang banyak kejadian suatu percobaan. Apa sih?
Setiap melakukan suatu percobaan pasti akan selalu mendapatkan hasil. Namun, tidak selalu hasil tersebut sesuai dengan yang diharapkan. Oleh karena itu dalam melakukan percobaan kita tentu harus menduga hasil yang mungkin terjadi. Dalam menentukan banyak kejadian suatu percobaan kita dapat menggunakan bantuan tabel dan diagram pohon.
Aturan Penjumlahan

Jika suatu kejadian pertama dapat terjadi dalam n1 cara yang berbeda, kejadian kedua dapat terjadi dalam n2 cara yang berbeda, dan seterusnya maka kejadian-kejadian itu secara berurutan dapat terjadi:
n1+n2+n3+ ...
Contoh:
Di rumah Anita terdapat 4 jenis sepeda, 3 jenis sepeda motor, dan 2 jenis mobil yang berbeda. Jika Anita ingin berpergian, ada banyak cara Anita menggunakan kendaraannya?
Pembahasan:
Pada kasus ini, ada 3 pilihan kendaraan yaitu sepeda, sepeda motor, dan mobil.Anita tidak mungkin menggunakan sekaligus ketiga jenis kendaraan tersebut.
Artinya Anita harus memilih salah satu jenis kendaraan saja.
Dengan demikian, banyak cara Anita menggunakan kendaraannya menggunakan aturan penjumlahan:
4 + 3 + 2 = 9 cara
Aturan Perkalian

Dalam memahami metode ini, kita dapat menjabarkannya menggunakan pasangan terurut. Jika suatu kejadian pertama dapat terjadi dalam n1 cara yang berbeda, kejadian kedua dapat terjadi dalam cara yang berbeda, dan seterusnya maka kejadian-kejadian itu secara berurutan dapat terjadi :
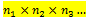
Contoh Soal:
Seorang karyawan memiliki 3 kemeja dan 2 celana yang masing-masing mempunyai warna berbeda.
Kemeja : Abu-abu, Putih, Merah
Celana : Biru, Hitam
Berapa banyak pasangan warna kemeja dan celana yang dapat dipakai?
Pembahasan:
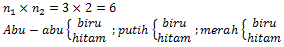
Banyaknya pasangan celana dan baju yang dapat dipakai yaitu:
{(abu-abu, biru), (abu-abu, hitam), (putih, biru), (putih, hitam), (merah, biru), (merah hitam)}
1.
Jawablah soal di bawah ini dengan benar!
Andin melemparkan tiga keping uang logam yang mempunyai sisi angka dan gambar secara bersamaan. Banyak kejadian yang mungkin terjadi adalah ….
A. 6
B. 7
C. 8
D. 9
E. 10
JAWABAN BENAR
C.
8
PEMBAHASAN
Banyak kejadian yang mungkin terjadi = 2n = 23 = 8
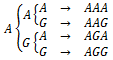
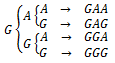
2.
Jawablah soal berikut dengan benar!
Di rumah Farhan terdapat 4 jenis sepeda, 3 jenis sepeda motor, dan 2 jenis mobil yang berbeda. Jika Farhan ingin berpergian, ada banyak cara Farhan menggunakan kendaraannya?
A. 6
B. 9
C. 10
D. 12
E. 24
JAWABAN BENAR
B.
9
PEMBAHASAN
Pada kasus ini, ada 3 pilihan kendaraan yaitu sepeda, sepeda motor, dan mobil. Farhan tidak mungkin menggunakan sekaligus ketiga jenis kendaraan tersebut. Artinya Farhan harus memilih salah satu jenis kendaraan saja. Dengan demikian, banyak cara Farhan menggunakan kendaraannya menggunakan aturan penjumlahan:
4 + 3 + 2 = 9 cara.
3.
Jawablah soal berikut dengan benar!
Sekolah X diwajibkan mengirimkan satu siswa untuk perwakilan mengikuti Olimpiade Matematika. Berapa banyaknya cara sekolah tersebut memilih siswa untuk perwakilan jika dalam tahap akhir seleksi terpilih 4 siswa perempuan dan 5 siswa laki-laki?
A. 5
B. 9
C. 12
D. 15
E. 20
JAWABAN BENAR
B.
9
PEMBAHASAN
Untuk menghitung banyaknya cara sekolah tersebut memilih siswa untuk perwakilan menggunakan kaidah penjumlahan sehingga 4 + 5 = 9 cara
4.
Jawablah soal di bawah ini dengan benar!
Seorang karyawan memiliki 3 kemeja dan 2 celana yang masing-masing mempunyai warna berbeda. Berapa banyak pasangan warna kemeja dan celana yang dapat dipakai?
A. 3
B. 5
C. 6
D. 8
E. 9
JAWABAN BENAR
C.
6
PEMBAHASAN
Banyaknya pasangan celana dan baju yang dapat dipakai yaitu:
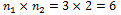
5.
Jawablah soal di bawah ini dengan tepat!
Jika nomor rumah yang terdiri atas dua angka tanpa angka nol, maka banyak rumah yang dimaksud dengan nomor genap adalah ….
A. 27
B. 36
C. 40
D. 45
E. 72
JAWABAN BENAR
B.
36
PEMBAHASAN
Jika pada soal banyak rumah yang dimaksud dengan nomor genap maka satuan dapat diisi oleh angka 2, 4, 6, 8.
Dengan demikian ada 4 cara untuk mengisi tempat satuan, sehingga n1 = 4.
Untuk puluhan dapat diisi dengan angka 1, 2, 3, 4, 5, 6, 7, 8, 9, sehingga n2 = 9.
Jadi, banyaknya nomor rumah dengan nomor genap adalah n1 x n2 = 4 x 9 = 36.

Oops!!!
Yah, jawaban kamu meleset nih. Ingin melihat pembahasan soal ini?

BENAR!!!
Selamat!
Jawaban kamu benar. Ingin lihat pembahasan soal ini?
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved

