Belajar Pintar Materi SMP, SMA, SMK
BelajarPintarV3
Matematika Wajib
Kaidah Pencacahan
MATERI
Notasi Faktorial


Sumber : PNG Download.id
Pernahkah Sobat Pintar duduk di meja bundar? Bagaimana kalian menentukan tempat duduknya? Kalau kamu ingin duduk di sebelah temanmu si A, tetapi si A ingin duduk di sebelah si B, bagaimana kemungkinan urutan tempat duduknya ya?
Banyaknya cara untuk duduk pada meja bundar dapat dihitung dengan menggunakan rumus permutasi lho, Sobat Pintar.
Dalam permutasi perlu dipahami terlebih dahulu terkait faktorial. Hasil kali bilangan bulat dari 1 sampai n adalah n! (dibaca : n faktorial) atau :
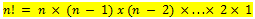
Contoh : 5! = 5 x 4 x 3 x 2 x 1 = 120
Permutasi

Sobat pintar, kali ini kita akan belajar tentang teori permutasi bilangan. Sebelumnya, apa yang kalian tahu tentang permutasi?
Permutasi adalah susunan berurutan dari semua atau sebagian elemen dari suatu himpunan.
Untuk menyelesaikan soal permutasi terdapat 4 metode, yaitu:
Permutasi dari Elemen yang Berbeda
Permutasi elemen dari elemen yang ada (setiap elemen berbeda) adalah susunan elemen itu dalam suatu urutan yang diperhatikan. Banyaknya permutasi dari elemen n diambil r elemen dapat dinotasikan:
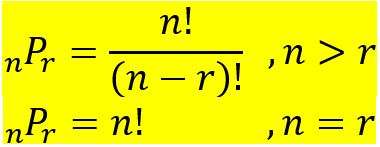
Sebagai ilustrasi: menyusun 3 elemen dari 3 huruf : a,b,c adalah a,b,c a,c,b b,c,a b,a,c c,a,b c,b,a dengan 3P3 = 3! = 6. Sedangkan menyusun 2 elemen dari 3 huruf adalah
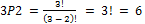
Permutasi dengan Berapa Elemen yang Sama
Setiap unsur yang digunakan tidak boleh lebih dari satu kali. Secara umum, banyaknya permutasi n elemen yang memuat k, l, m, … elemen yang sama dapat dinotasikan:
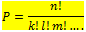
sebagai ilustrasi : ada 3 bola basket dan 2 bola kasti.
Jumlah cara menyusunnya adalah:
p = n! / (n1! n2! ... nr!) = 6! / (3! 2!) = 6 x 5 x 4 x 3! / 3! x (2 x 1) = 60
Permutasi Siklis
Permutasi siklis digunakan untuk menghitung banyak cara yang dibuat dari susunan melingkar. Secara umum, banyaknya permutasi siklis dapat dinotasikan:
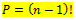
sebagai ilustrasinya misal : bagaimana banyaknya cara 4 orang duduk melingkar dalam 1 meja makan adalah :
P = (4 - 1)! = 3! = 3 x 2 x 1 = 6
Permutasi Berulang
Permutasi berulang adalah permutasi yang dalam penyusunannya urutan diperhatikan dan suatu objek dapat dipilih lebih dari sekali (berulang). Banyaknya permutasi ini dinotasikan:
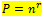
Berbeda dengan permutasi yang tidak boleh berulang dapat dinotasikan:
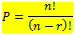
Nah Sobat, gimana nih? Mudah bukan?
Yuk kita lanjut latihan soal!
1.
Jawablah soal di bawah ini dengan tepat !
Menjelang Pergantian kepengurusan BEM STMIK Tasikmalaya akan dibentuk panitia inti sebanyak 2 orang (terdiri dari ketua dan wakil ketua), calon panitia tersebut ada 6 orang yaitu: a, b, c, d, e, dan f. Ada berapa pasang calon yang dapat duduk sebagai panitia inti tersebut?
A. 20
B. 30
C. 40
D. 50
E. 60
JAWABAN BENAR
B.
30
PEMBAHASAN
6P2 = 6! / (6-2)!
= (6.5.4.3.2.1) / (4.3.2.1)
= 720 / 24
= 30 cara
2.
Jawablah soal di bawah ini dengan tepat!
Berapa banyaknya permutasi dari cara duduk yang dapat terjadi jika 8 orang disediakan 4 kursi, sedangkan salah seorang dari padanya selalu duduk di kursi tertentu?
A. 180 cara
B. 200 cara
C. 210 cara
D. 220 cara
E. 250 cara
JAWABAN BENAR
C.
210 cara
PEMBAHASAN
Jika salah seorang selalu duduk di kursi tertentu maka tinggal 7 orang dengan 3 kursi kosong.
Maka banyaknya cara duduk ada :
7P3 = 7!/(7-3)!
= 7!/4!
= 7.6.5
= 210 cara
3.
Jawablah soal di bawah ini dengan tepat !
Ada berapa cara 5 gelas warna yang mengitari meja kecil, dapat menempati kelima tempat dengan urutan yang berlainan?
A. 18 cara
B. 20 cara
C. 22 cara
D. 24 cara
E. 26 cara
JAWABAN BENAR
D.
24 cara
PEMBAHASAN
P(siklis) = (5-1)! = 4! = 4 . 3 . 2 . 1 = 24 cara
4.
Jawablah soal si bawah ini dengan tepat!
Dari 7 orang calon termasuk Astro akan dipilih 4 orang sebagai pengurus kelas, yaitu sebagai ketua, wakil, sekretaris, dan bendahara. Banyaknya susunan pengurus kelas yang mungkin terjadi jika Astro harus menjadi ketua kelas adalah ….
A. 36
B. 60
C. 120
D. 336
E. 450
JAWABAN BENAR
C.
120
PEMBAHASAN
Banyaknya susunan adalah
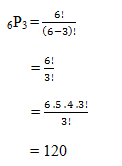
5.
Jawablah soal di bawah ini dengan tepat!
Berapa banyak susunan huruf yang berbeda dapat dibentuk dari huruf-huruf pada kata LILIN?
A. 10
B. 15
C. 25
D. 30
E. 45
JAWABAN BENAR
D.
30
PEMBAHASAN
Banyaknya susunan adalah menggunakan permutasi unsur yang sama yaitu:
Jumlah huruf LILIN = n = 5
Unsur yang sama yaitu;
Huruf L= 2 dan huruf I = 2
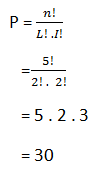

Oops!!!
Yah, jawaban kamu meleset nih. Ingin melihat pembahasan soal ini?

BENAR!!!
Selamat!
Jawaban kamu benar. Ingin lihat pembahasan soal ini?
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved

