Belajar Pintar Materi SMP, SMA, SMK
BelajarPintarV3
Matematika
Trigonometri
MATERI
Relasi 2 Sudut Lancip
Untuk memudahkan sobat pintar menyelidiki relasi nilai perbandingan trigonometri tersebut, perhatikan gambar dan penjelasan berikut ini
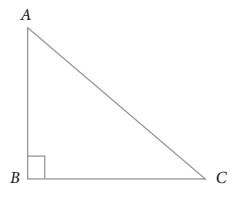
karena 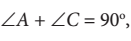 sehingga
sehingga 
sehingga dapat diperoleh
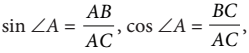
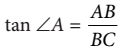
selain itu, sobat pintar juga dapat menuliskan
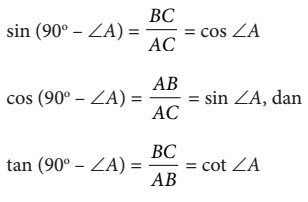
Relasi dua sudut yang lancip dapat dituliskan sebagai berikut

Kemudian jika relasi sudut  pada kuadaran II, dapat ditulis
pada kuadaran II, dapat ditulis
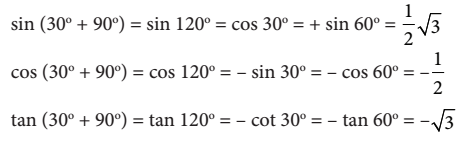
Kemudian jika relasi sudut  pada kuadran III, dapat ditulis
pada kuadran III, dapat ditulis
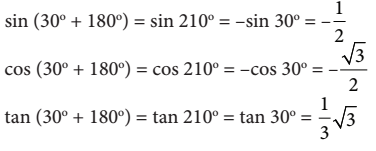
Jika relasi sudut  pada kuadran IV, dapat ditulis
pada kuadran IV, dapat ditulis

Jika relasi sudut  pada kuadran I, dapat ditulis
pada kuadran I, dapat ditulis
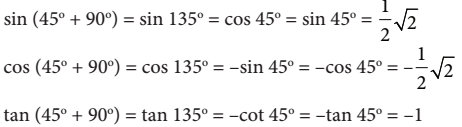
jika relasi sudut  pada kuadran III, dapat ditulis
pada kuadran III, dapat ditulis
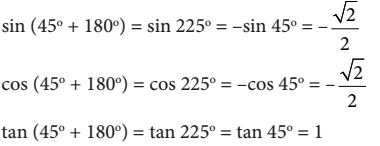
Dengan demikian, diperoleh bahwa
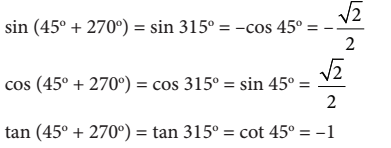
Untuk 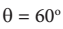 dengan cara yang sama dapat diperoleh kesimpulan bahwa
dengan cara yang sama dapat diperoleh kesimpulan bahwa
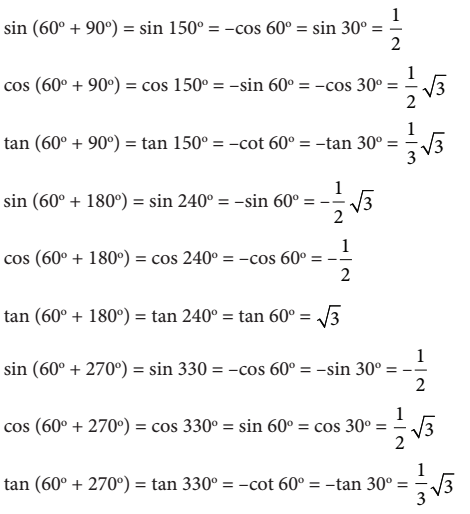
Nilai perbandingan nilai trigonometri untuk sudut-sudut istimewa
Berikut adalah nilai perbandingan nilai trigonometri untuk sudut istimewa supaya sobat pintar lebih mudah memahaminya
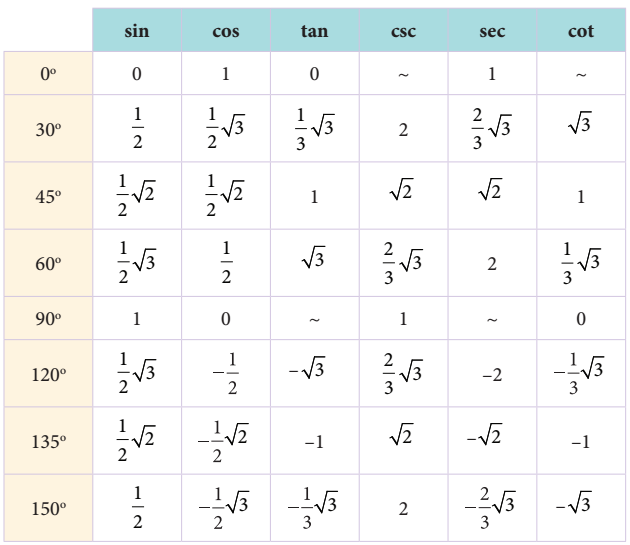
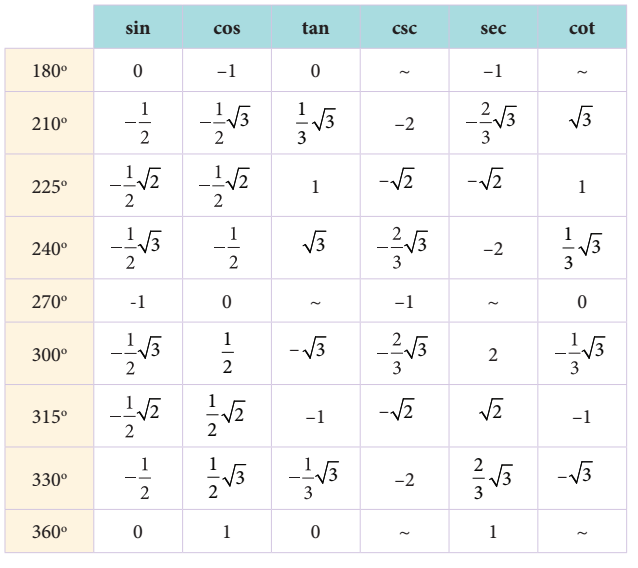
Sifat-sifat Trigonometri
Dengan memperhatikan secara cermat nilai-nilai pada tabel dan letaknya pada kuadran yang sudah di paparkan sebelumnya, maka dapat disimpulkan seperti dalam sifat berikut

Tanda positif dan negatif di setiap kuadran di atas diberikan untuk membantu sobat pintar mengingat nilai-nilai perbandingan trigonometri, Sifat di atas, hal penting dan yang lain juga dapat disimpulkan, yaitu sifat relasi antarsudut, seperti disimpulkan pada sifat berikut.
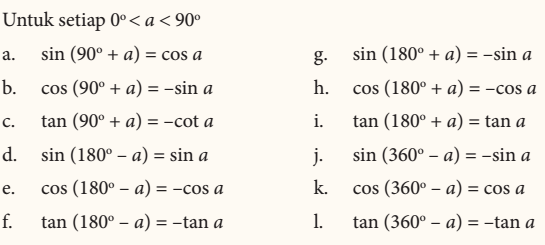
Identitas Trigonometri

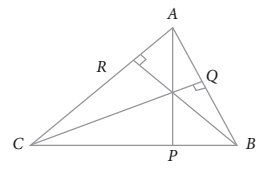
Untuk setiap segitiga, dengan 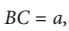
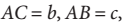 dengan sudut-sudutnya
dengan sudut-sudutnya 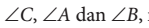 maka berlaku
maka berlaku
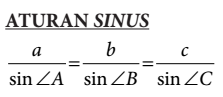

1.
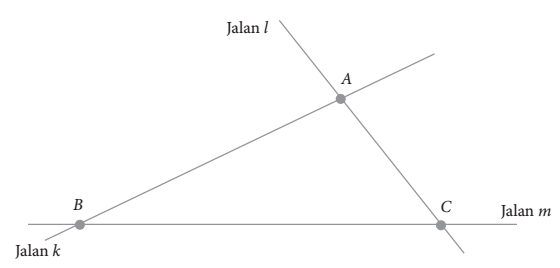
Jalan k dan jalan l berpotongan di kota A. Dinas tata ruang kota ingin menghubungkan kota B dengan kota C dengan membangun jalan m dan memotong kedua jalan yang ada, seperti yang ditunjukkan Gambar dibawah. Jika jarak antara kota A dan kota C adalah 5 km, sudut yang dibentuk jalan m dengan jalan l adalah  dan sudut yang dibentuk jalan k dan jalan m adalah
dan sudut yang dibentuk jalan k dan jalan m adalah 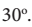 Tentukan jarak kota A dengan kota B.
Tentukan jarak kota A dengan kota B.
A. 9,4 Km
B. 10,9 Km
C. 11,7 Km
D. 8 Km
E. 12 Km
JAWABAN BENAR
A.
9,4 Km
PEMBAHASAN


2.
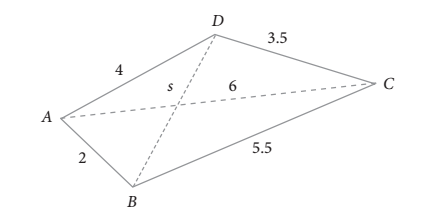
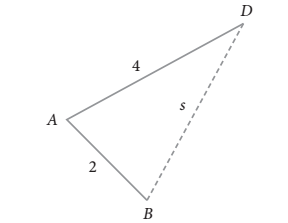
Tentukan nilai s
A. 4,7
B. 2,5
C. 3,8
D. 8,8
E. 2
JAWABAN BENAR
A.
4,7
PEMBAHASAN
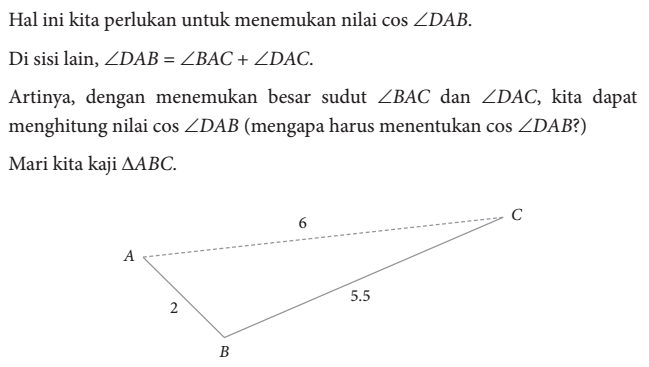
dengan menggunakan aturan cosinus maka,
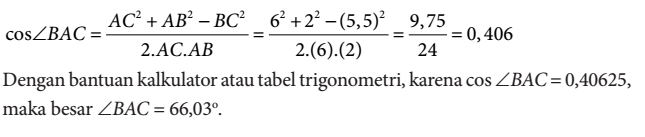
dengan aturan cosinus, maka diperoleh

Sehingga panjang sisi s adalah


Oops!!!
Yah, jawaban kamu meleset nih. Ingin melihat pembahasan soal ini?

BENAR!!!
Selamat!
Jawaban kamu benar. Ingin lihat pembahasan soal ini?
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved

