Belajar Pintar Materi SMP, SMA, SMK
BelajarPintarV3
UTBK - SNBT
Penalaran Matematika
MATERI
Aritmatika Sosial

Untung
- Definisi: Keuntungan terjadi jika harga jual lebih besar daripada harga beli.
- Rumus Keuntungan:
Keuntungan = Harga Jual - Harga Beli - Persentase Keuntungan:
Persentase Keuntungan = Keuntungan/Harga Beli x 100%
Contoh Soal:
Ani membeli barang seharga Rp200.000, kemudian menjualnya dengan harga Rp250.000. Berapa persen keuntungan Ani?
Penyelesaian:
Keuntungan = Rp250.000 - Rp200.000 = Rp50.000
Persentase Keuntungan = Rp50.000/Rp200.000 x 100% = 25%
Rugi
- Definisi: Kerugian terjadi jika harga jual lebih kecil daripada harga beli.
- Rumus Kerugian:
Kerugian = Harga Beli - Harga Jual - Persentase Kerugian:
Persentase Kerugian = Kerugian/Harga Beli x 100%
Contoh Soal:
Sebuah barang dibeli seharga Rp300.000, lalu dijual seharga Rp250.000. Berapa persen kerugiannya?
Penyelesaian:
Kerugian = Rp300.000 - Rp250.000 = Rp50.000
Persentase Kerugian = Rp50.000/Rp300.000 x 100% = 16,67%
Diskon
- Definisi: Pengurangan harga dari harga awal.
- Rumus Diskon:
Harga Diskon = Harga Awal x Persentase Diskon/100 - Harga Setelah Diskon:
Harga Akhir = Harga Awal - Harga Diskon
Contoh Soal:
Sebuah barang berharga Rp500.000 mendapat diskon 20%. Berapa harga setelah diskon?
Penyelesaian:
Harga Diskon = Rp500.000 x 20/100 = Rp100.000
Harga Akhir = Rp500.000 - Rp100.000 = Rp400.000
Bunga Tunggal dan Bunga Majemuk
Bunga Tunggal:
Definisi: Bunga yang dihitung dari modal awal setiap periode.
Rumus:
B = P x r x t
M = P + B
Di mana:
B: Bunga,
P: Modal awal,
r: Suku bunga (dalam desimal),
t: Waktu (tahun).
Contoh Soal:
Modal Rp10.000.000 disimpan di bank dengan bunga tunggal 6% per tahun selama 3 tahun. Berapa total uang setelah 3 tahun?
Penyelesaian:
B = Rp10.000.000 x 0,06 x 3 = Rp1.800.000
M = Rp10.000.000 + Rp1.800.000 = Rp11.800.000
Bunga Majemuk:
Definisi: Bunga yang dihitung dari modal awal dan bunga yang telah diakumulasi.
Rumus:
M=P x (1 + r)t
Di mana M: Nilai akhir.
Contoh Soal:
Modal Rp10.000.000 disimpan dengan bunga majemuk 6% per tahun selama 3 tahun. Berapa total uang setelah 3 tahun?
Penyelesaian:
M = Rp10.000.000 x (1 + 0,06)3 = Rp10.000.000 x 1,191016 = Rp11.910.160
Perbandingan

Perbandingan adalah cara untuk membandingkan dua atau lebih nilai untuk mengetahui hubungan antar nilai tersebut. Dalam matematika, perbandingan sering digunakan untuk menyelesaikan berbagai masalah kehidupan sehari-hari, seperti kecepatan, harga, atau jarak.
Terdapat dua jenis perbandingan utama, yaitu:
Perbandingan Senilai
Perbandingan senilai adalah hubungan antara dua besaran yang meningkat atau menurun secara bersamaan. Artinya, jika salah satu besaran bertambah, maka besaran lainnya juga bertambah dengan proporsi yang sama, begitu pula jika berkurang.
Ciri-Ciri Perbandingan Senilai
- Nilai kedua besaran bertambah atau berkurang secara bersamaan.
- Rasio (perbandingan) antara dua besaran selalu konstan.
Rumus Perbandingan Senilai
Jika A dan B adalah dua besaran yang memiliki hubungan perbandingan senilai, maka:
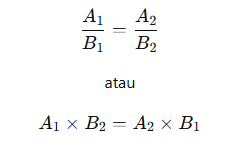
Contoh Soal
Sebuah mobil memerlukan 4 liter bensin untuk menempuh 80 km. Berapa liter bensin yang dibutuhkan untuk menempuh 200 km?
Diketahui:
- A1 = 4 liter
- B1 = 80 km
- B2 = 200 km
Gunakan rumus:
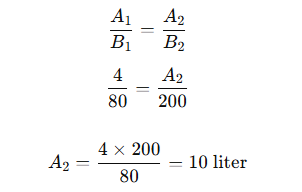
Perbandingan Berbalik Nilai
Perbandingan berbalik nilai adalah hubungan antara dua besaran di mana jika salah satu besaran bertambah, maka besaran lainnya berkurang, dan sebaliknya, dengan proporsi yang tetap.
Ciri-Ciri Perbandingan Berbalik Nilai
- Salah satu besaran bertambah, sementara yang lain berkurang.
- Hasil kali antara dua besaran selalu konstan.
Rumus Perbandingan Berbalik Nilai
Jika A dan B adalah dua besaran yang memiliki hubungan perbandingan berbalik nilai, maka:
A1 x B1 = A2 x B2
Contoh Soal
Sebuah pekerjaan dapat diselesaikan oleh 5 orang dalam waktu 12 hari. Berapa hari yang dibutuhkan jika pekerja ditambah menjadi 10 orang?
Diketahui:
- A1 = 5 orang
- B1 = 12 hari
- A2 = 10 orang
Gunakan rumus:
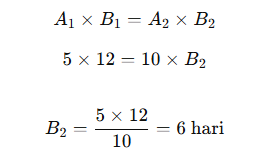
Baris Aritmatika dan Geometri

Aritmatika
Definisi: Barisan dengan beda antar suku yang tetap.
Rumus Barisan Aritmatika:
Suku ke-n:
Un = a + (n - 1)b
Di mana:
a: Suku pertama,
b: Beda,
n: Nomor suku.
Jumlah n-suku:
Sn = n/2 x (2a + (n - 1)b)
Contoh Soal:
Diketahui barisan aritmatika dengan a=3, b=5. Hitung suku ke-10 dan jumlah 10 suku pertama!
Penyelesaian:
U10 = 3 + (10 - 1)5 = 3 + 45 = 48
S10 = 10/2 x (2 x 3 + (10 - 1)5) = 5 x (6 + 45) = 5 x 51 = 255
Geometri
Definisi: Barisan dengan rasio antar suku yang tetap.
Rumus Barisan Geometri:
Suku ke-n:
Un = a x rn-1
Di mana:
a: Suku pertama,
r: Rasio,
n: Nomor suku.
Jumlah n-suku:
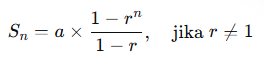
Contoh Soal:
Diketahui barisan geometri dengan a = 2, r=3. Hitung suku ke-5 dan jumlah 5 suku pertama!
Penyelesaian:
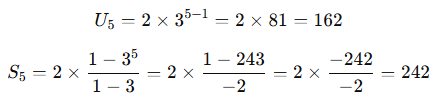
Sistem Persamaan Linear

Sistem Dua Variabel
- Definisi: Persamaan dengan dua variabel yang dicari penyelesaiannya.
- Bentuk Umum:
a1x + b1y = c1, a2x + b2y = c2
Metode Penyelesaian:
- Substitusi
- Eliminasi
- Grafik
Contoh Soal:
Diketahui:
- 2x + y = 10
- x - y = 4
- Cari x dan y!
Penyelesaian:
Dari x - y = 4, diperoleh x = y + 4.
Substitusi ke 2x + y = 10:
2(y + 4) + y = 10 --> 2y + 8 + y = 10 --> 3y = 2 --> y = 2/3
x = y + 4 = 2/3 + 4 = 14/3
Sistem Tiga Variabel
- Definisi: Persamaan dengan tiga variabel yang dicari penyelesaiannya.
- Bentuk Umum:
a1x + b1y + c1z = d1 - Diselesaikan dengan substitusi atau eliminasi bertahap.
Fungsi

Definisi Fungsi
Relasi dari satu himpunan ke himpunan lain yang memasangkan setiap elemen domain dengan satu elemen kodomain.
Notasi
f(x) = ax + b (fungsi linear)
f(x)=ax2 + bx + c (fungsi kuadrat)
Komposisi Fungsi
Rumus:
(f o g)(x) = f(g(x))
Invers Fungsi
Jika f(x) = y, maka invers f-1(y) = x.
Langkah: Tukar x dan y, lalu selesaikan untuk y.
Contoh Soal:
Jika f(x) = 2x + 3, tentukan f-1(x)!
Penyelesaian:
y = 2x + 3 --> x = 2y + 3 --> y = (x - 3)/2
f-1(x)= (x - 3)/2
1.
Kerjakan soal berikut ini dengan tepat!
Seorang pedagang barang antik memasang harga jual guci keramik dengan 10% lebih mahal dari harga ia membelinya. Selama ia promosi, ia memberi diskon 5% dari harga jual. Berapa keuntungannya dibandingkan dengan harga beli?
A. Rugi 5%
B. Rugi 10%
C. Rugi 15%
D. Untung 5%
E. Untung 10%
JAWABAN BENAR
D.
Untung 5%
PEMBAHASAN
Persentase harga jual barang = persentase harga beli + persentase keuntungan
= 100% + 10%
= 110%.
Persentase harga jual barang setelah promosi
= persentase harga jual barang – persentase diskon
= 110% - 5%
= 105%.
Persentase keuntungannya dibandingkan harga beli adalah 5% lebih banyak.
2.
Kerjakanlah soal di bawah ini!
Diketahui suatu deret aritmatika dengan suku tengah yaitu 32. Jika jumlah n suku pertama deret tersebut adalah 672, maka banyak suku dalam deret tersebut adalah ….
A. 12
B. 16
C. 17
D. 21
E. 24
JAWABAN BENAR
E.
24
PEMBAHASAN

3.
Kerjakanlah soal di bawah ini!
Sesorang mahasiswa membutuhkan waktu 16,1 menit untuk pergi ke kampus dengan jalan kaki. Jika menggunakan sepeda, ia hanya membutuhkan waktu 2 menit 20 detik. Pada suatu hari, ia ke kampus mengendaai sepeda. Setelah 1 2/3 menit ia bersepeda, tiba-tiba bannya bocor. Terpaksa ia harus melanjutkan perjalanannya dengan jalan kaki. Waktu yang dibutuhkan olehnya untuk melanjutkan perjalanannya sampai ke kampus adalah ....
A. 276 detik
B. 267 detik
C. 176 detik
D. 167 detik
E. 116 detik
JAWABAN BENAR
A.
276 detik
PEMBAHASAN
t jalan kaki = 16,1 menit = 966 detik
t sepeda = 2 menit 20 detik = 140 detik
jarak ke kampus diibaratkan = 1
1 2/3 menit = 100 detik
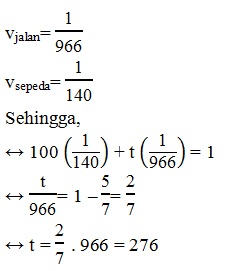
Jawaban: A
4.
Kerjakanlah soal di bawah ini!
Untuk membuat sebuah baju dibutuhkan kain dengan panjang 1,5 meter dan lebar 1 meter serta 8 buah kancing. Pada suatu hari telah dihabiskan 144 kancing. Panjang kain yang telah digunakan jika lebarnya 3 meter adalah ....
A. 9 meter
B. 12 meter
C. 24 meter
D. 47 meter
E. 48 meter
JAWABAN BENAR
A.
9 meter
PEMBAHASAN
Produksi harian 144/8 = 18 buah baju
Luasan kain yang dibutuhkan adalah : 18 x 1,5 x 1 = 27 m2
Jadi jika lebar kain 3 meter, maka panjang kainnya adalah 27/3 = 9 meter.
Jawaban A
5.
Kerjakanlah soal di bawah ini!
Diketahui suatu deret aritmatika dengan suku tengah yaitu 32. Jika jumlah n suku pertama deret tersebut adalah 672, maka banyak suku dalam deret tersebut adalah ….
A. 12
B. 16
C. 17
D. 21
E. 24
JAWABAN BENAR
E.
24
PEMBAHASAN


Oops!!!
Yah, jawaban kamu meleset nih. Ingin melihat pembahasan soal ini?

BENAR!!!
Selamat!
Jawaban kamu benar. Ingin lihat pembahasan soal ini?
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved

