Belajar Pintar Materi SMP, SMA, SMK
BelajarPintarV3
UTBK - SNBT
Penalaran Umum
MATERI
Proposisi/Pernyataan

Proposisi sederhana adalah pernyataan yang memiliki nilai kebenaran (benar atau salah) dan tidak dapat diuraikan lagi menjadi pernyataan lain.
Proposisi Sederhana
Proposisi sederhana adalah pernyataan tunggal yang tidak memiliki penghubung logis.
Contoh:
- "Matahari terbit di timur." (Benar)
- "2 + 2 = 5." (Salah)
Proposisi Majemuk
Proposisi majemuk adalah gabungan dari dua atau lebih proposisi sederhana yang dihubungkan oleh kata penghubung logis.
Konjungsi (AND)
Menghubungkan dua proposisi dengan "dan". Proposisi majemuk bernilai benar jika kedua proposisi bernilai benar.
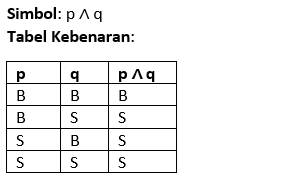
Contoh:
"Hari ini hujan dan angin kencang."
Disjungsi (OR)
Menghubungkan dua proposisi dengan "atau". Proposisi majemuk bernilai benar jika salah satu atau kedua proposisi bernilai benar.
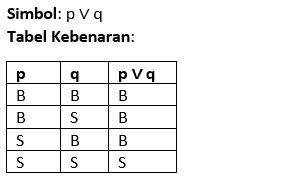
Contoh:
"Besok akan hujan atau cerah."
Implikasi (Jika... maka..., -->)
Proposisi majemuk berbentuk sebab-akibat. Proposisi bernilai salah hanya jika antecedent (p) benar dan consequent (q) salah.
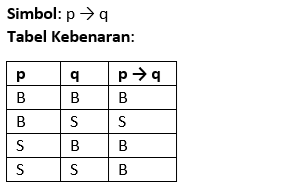
Contoh:
"Jika saya belajar, maka saya akan lulus."
Biimplikasi (Jika dan hanya jika, <-->)
Proposisi bernilai benar jika kedua proposisi memiliki nilai kebenaran yang sama.
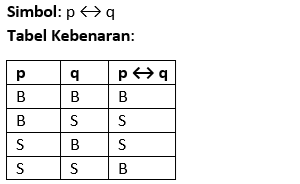
Contoh:
"Saya lulus jika dan hanya jika saya belajar."
Negasi/Ingkaran

Negasi adalah pernyataan yang memiliki nilai kebenaran kebalikan dari proposisi asal.
Simbol: -p
Contoh:
- Proposisi: "Hari ini hujan."
- Negasi: "Hari ini tidak hujan."
Negasi Proposisi Majemuk

Aturan Penarikan Kesimpulan

Berikut beberapa aturan dalam logika deduktif:
Modus Ponens
Jika p--> q dan p benar, maka q juga benar.
Contoh:
- Premis 1: Jika hujan (p), maka jalan basah (q).
- Premis 2: Hujan (p).
- Kesimpulan: Jalan basah (q).
Modus Tollens
Jika p --> q dan -q benar, maka -p juga benar.
Contoh:
- Premis 1: Jika hujan (p), maka jalan basah (q).
- Premis 2: Jalan tidak basah (-q).
- Kesimpulan: Tidak hujan (-p).
Silogisme Hipotesis
Jika p --> q dan q --> r, maka p --> r.
Contoh:
- Premis 1: Jika belajar (p), maka paham (q).
- Premis 2: Jika paham (q), maka lulus (r).
- Kesimpulan: Jika belajar (p), maka lulus (r).
Kondisi tanpa Kesimpulan

Ada beberapa kondisi atau bentuk dua premis yang tidak dapat ditarik kesimpulan berdasarkan aturan logika deduktif yang ada. Berikut adalah beberapa contoh situasi di mana dua premis tidak dapat ditarik kesimpulannya:
Tidak ada hubungan logis langsung antara kedua premis
Jika dua premis tidak memiliki hubungan implikatif yang jelas (seperti dalam modus ponens atau modus tollens), maka tidak ada kesimpulan yang bisa ditarik.
Contoh:
- Premis 1: Semua burung bisa terbang.
- Premis 2: Kucing adalah hewan peliharaan.
- Kesimpulan?: Tidak ada kesimpulan yang valid karena kedua premis tidak terkait secara langsung.
Premis tidak cukup untuk menarik kesimpulan
Terkadang dua premis yang tampaknya benar tidak memberikan cukup informasi untuk menarik kesimpulan yang sah.
Contoh:
- Premis 1: Semua manusia adalah makhluk hidup.
- Premis 2: Semua makhluk hidup membutuhkan oksigen.
- Kesimpulan?: Tidak dapat disimpulkan secara langsung bahwa semua manusia membutuhkan oksigen. Meskipun kedua premis benar, untuk menarik kesimpulan ini, diperlukan premis tambahan yang lebih spesifik tentang manusia.
Premis mengandung kontradiksi internal
Jika dua premis saling bertentangan, maka tidak mungkin ada kesimpulan yang sah yang dapat diambil. Hal ini terkait dengan prinsip non-kontradiksi dalam logika.
Contoh:
- Premis 1: Semua siswa lulus ujian.
- Premis 2: Ada siswa yang gagal ujian.
- Kesimpulan?: Tidak ada kesimpulan yang valid, karena kedua premis bertentangan satu sama lain.
Premis tidak memenuhi aturan logika yang berlaku
Beberapa bentuk proposisi atau hubungan antara premis tidak mengikuti aturan logika yang sah, seperti jika sebuah implikasi tidak cukup dijelaskan atau premis tidak diikuti aturan yang benar.
Contoh:
- Premis 1: Jika hujan, maka jalanan basah.
- Premis 2: Jalanan basah.
- Kesimpulan?: Tidak dapat disimpulkan dengan cara yang valid bahwa hujan (karena ini adalah kesalahan yang dikenal dengan fallacy "affirming the consequent").
Dengan demikian, dua premis bisa jadi tidak dapat menghasilkan kesimpulan yang sah jika hubungan antar premisnya tidak logis atau ada kontradiksi dalam premis-premis tersebut.
Pernyataan Berkuantor

Jenis-Jenis Kuantor
- Kuantor Universal ("semua" atau "setiap")
Bentuk umum: "Semua A adalah B", Artinya: Setiap anggota himpunan A memiliki sifat B.
Contoh:- Semua siswa rajin belajar.
- Setiap manusia membutuhkan oksigen.
- Kuantor Eksistensial ("ada" atau "beberapa")
Bentuk umum: "Beberapa A adalah B", Artinya: Ada minimal satu anggota himpunan A yang memiliki sifat B.
Contoh:- Beberapa siswa pandai bermain musik.
- Ada tanaman yang bisa hidup tanpa banyak air.
Konversi dan Logika Pernyataan
- Negasi Pernyataan
- Negasi kuantor universal: "Semua A adalah B" --> "Ada A yang bukan B"
- Negasi kuantor eksistensial: "Ada A yang B" --> "Tidak ada A yang B"
- Contoh:
Semua burung bisa terbang --> Negasi: Ada burung yang tidak bisa terbang.
- Implikasi
Jika ada hubungan kausal atau sebab-akibat antara dua pernyataan, maka implikasi digunakan.
Contoh: Jika semua A adalah B, maka tidak ada A yang bukan B.
Aturan Penarikan Kesimpulan dari Dua Pernyataan Berkuantor
Dalam logika, penarikan kesimpulan dari dua pernyataan berkuantor dilakukan berdasarkan hubungan logis antara premis-premis yang diberikan. Berikut adalah aturan dasarnya:
- Aturan Kuantor Universal (Semua/Setiap)
Format Umum: Jika Semua A adalah B dan Semua B adalah C, maka kesimpulannya adalah Semua A adalah C.
Contoh:- Premis 1: Semua manusia adalah makhluk hidup.
- Premis 2: Semua makhluk hidup membutuhkan oksigen.
- Kesimpulan: Semua manusia membutuhkan oksigen.
- Aturan Kuantor Eksistensial (Ada/Beberapa)
Format Umum:
Jika Ada A yang B dan Semua B adalah C, maka kesimpulannya adalah Ada A yang C.
Contoh:- Premis 1: Ada siswa yang pandai bermain musik.
- Premis 2: Semua orang yang pandai bermain musik mencintai seni.
- Kesimpulan: Ada siswa yang mencintai seni.
- Aturan Gabungan Kuantor Universal dan Eksistensial
Format Umum: Jika Semua A adalah B dan Ada B yang C, maka tidak ada kesimpulan pasti tentang hubungan langsung antara A dan C.
Catatan: Pernyataan ini tidak selalu memberikan hubungan langsung karena sifat eksistensial tidak menjamin hubungan terhadap semua elemen A.
Contoh:- Premis 1: Semua siswa rajin belajar.
- Premis 2: Ada siswa yang gemar olahraga.
- Kesimpulan: Tidak dapat disimpulkan bahwa semua siswa gemar olahraga.
- Silogisme Kuantor
Format Umum:
Jika Semua A adalah B dan Semua B adalah C, maka Semua A adalah C (logika transitif).
Jika Semua A adalah B dan Tidak ada B yang C, maka Tidak ada A yang C.- Contoh (Kasus Positif):
- Premis 1: Semua dokter mempelajari anatomi.
- Premis 2: Semua orang yang mempelajari anatomi memahami tubuh manusia.
- Kesimpulan: Semua dokter memahami tubuh manusia.
- Contoh (Kasus Negatif):
- Premis 1: Semua ikan hidup di air.
- Premis 2: Tidak ada makhluk yang hidup di darat yang adalah ikan.
- Kesimpulan: Tidak ada ikan yang hidup di darat.
- Contoh (Kasus Positif):
- Aturan Penolakan Kesimpulan Tidak Valid
Kesalahan Umum: Tidak semua kombinasi premis dapat menghasilkan kesimpulan yang valid. Contohnya:- Premis 1: Semua burung bisa terbang.
- Premis 2: Ada hewan yang bisa terbang.
- Kesimpulan (Tidak Valid): Tidak dapat disimpulkan bahwa semua hewan yang bisa terbang adalah burung.
- Penarikan Kesimpulan dengan Negasi
Negasi perlu diperhatikan dengan hati-hati, terutama dalam hubungan kuantor universal dan eksistensial.
Format Umum:
Jika Tidak ada A yang B dan Semua B adalah C, maka Tidak ada A yang C. Contoh:- Premis 1: Tidak ada pohon yang bisa berjalan.
- Premis 2: Semua yang bisa berjalan adalah makhluk hidup.
- Kesimpulan: Tidak ada pohon yang adalah makhluk hidup.
1.
Jawablah pertanyaan berikut!
Pupuk memiliki unsur yang berguna bagi tanaman.
X adalah pupuk.
Kesimpulan yang benar adalah ?
A. X memiliki unsur yang berguna bagi tanaman
B. X tidak memiliki unsur yang berguna bagi tanaman
C. Bukan X yang memiliki unsur yang berguna bagi tanaman
D. Kecuali X, pupuk memiliki unsur yang berguna bagi tanaman
E. Hanya X yang tidak memiliki unsur yang berguna bagi tanaman
JAWABAN BENAR
A.
X memiliki unsur yang berguna bagi tanaman
PEMBAHASAN
Karena X adalah pupuk, maka X memiliki unsur yang berguna bagi tanaman.
Jawaban A
2.
Jawablah pertanyaan berikut!
Ketika belajar di ruang B atau C, semua orang menggunakan kipas angin.
Alex belajar di ruang B.
Kesimpulan yang benar adalah ?
A. Alex menggunakan kipas angin
B. Alex tidak menggunakan kipas angin
C. Alex menggunakan bukan kipas angin
D. Bukan Alex yang menggunakan kipas angin
E. Alex menggunakan alat kecuali kipas angin
JAWABAN BENAR
A.
Alex menggunakan kipas angin
PEMBAHASAN
Karena Alex belajar di ruang B, maka Alex menggunakan kipas angin.
Jawaban A
3.
Jawablah pertanyaan berikut!
Semua yang teringat, pernah dicatat.
Sebagian pengalaman pahit masih teringat.
Kesimpulan yang benar adalah ?
A. Semua pengalaman pahit pernah dicatat
B. Sebagian pengalaman pahit pernah dicatat
C. Semua pengalaman pahit adalah yang teringat
D. Semua yang pernah dicatat adalah yang teringat
E. Semua yang pernah dicatat adalah pengalaman pahit
JAWABAN BENAR
B.
Sebagian pengalaman pahit pernah dicatat
PEMBAHASAN
P1 : Semua yang teringat, pernah dicatat.
P2 : Sebagian pengalaman pahit masih teringat.
K : Sebagian pengalaman pahit pernah dicatat.
Jawaban B
4.
Pilihlah jawaban yang paling tepat!
Kevin menyukai Fisika, ia ingin kuliah dijurusan Teknik Nuklir.
Russel, teman sekelas Kevin, menyukai Fisika.
Kesimpulan mana yang benar?
A. Kevin dan Russel belajar Fisika bersama.
B. Kevin dan Russel ingin kuliah jurusan Teknik Nuklir.
C. Kevin dan Russel menyukai Teknik Nuklir.
D. Kevin dan Russel belajar Fisika di Teknik Nuklir.
E. Kevin dan Russel menyukai Fisika.
JAWABAN BENAR
E.
Kevin dan Russel menyukai Fisika.
PEMBAHASAN
P1 : Kevin menyukai Fisika, ia ingin kuliah di jurusan Teknik Nuklir.
P2 : Russel, teman sekelas Kevin, menyukai Fisika.
S : Kevin dan Russel menyukai Fisika
5.
Jawablah pertanyaan berikut!
Jika dekan menulis jurnal di ruangannya, maka dekan tidak menggunakan laptopnya.
Jika dekan tidak menggunakan laptopnya, maka dekan akan kesulitas menulis jurnal.
Siang ini dekan tidak menggunakan laptopnya.
Kesimpulan mana yang benar?
A. Dekan tidak bisa menulis jurnal.
B. Siang ini dekan menulis jurnal.
C. Dekan tidak menulis jurnal siang ini.
D. Siang ini dekan akan kesulitan menulis jurnal.
E. Dekan menulis jurnal di ruangannya.
JAWABAN BENAR
D.
Siang ini dekan akan kesulitan menulis jurnal.
PEMBAHASAN
P1 : Jika dekan menulis jurnal di ruangannya, maka dekan tidak menggunakan laptopnya
P2 : Jika dekan tidak menggunakan laptopnya, maka dekan akan kesulitan meulis jurnal
P3 : Siang ini dekan tidak menggunakan laptopnya
S : Siang ini dekan akan kesulitan menulis jurnal

Oops!!!
Yah, jawaban kamu meleset nih. Ingin melihat pembahasan soal ini?

BENAR!!!
Selamat!
Jawaban kamu benar. Ingin lihat pembahasan soal ini?
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved

