Belajar Pintar Materi SMP, SMA, SMK
BelajarPintarV3
UTBK - SNBT
Penalaran Umum
MATERI
Aritmatika

Operasi Dasar: Penjumlahan, pengurangan, perkalian, dan pembagian.
- Contoh: Hitung hasil dari 72 / 8 + 15 x 3.
- Strategi: Gunakan urutan operasi (prioritas) dengan benar, yaitu kurung, pangkat, perkalian/pembagian, kemudian penjumlahan/pengurangan (aturan BODMAS).
Pecahan: Penjumlahan, pengurangan, perkalian, dan pembagian pecahan.
- Contoh: Berapa hasil dari (1/3) + (1/5) + (1/6) ?
- Strategi: Samakan penyebut pecahan sebelum melakukan operasi, lalu sederhanakan hasilnya.
Persentase:
- Contoh: Sebuah barang didiskon 20% dari harga Rp500.000. Berapa harga setelah diskon?
- Strategi: Gunakan rumus % x nilai
Bilangan Bulat dan Desimal:
- Contoh: Tentukan hasil dari 3,25 x 4,1.
- Strategi: Kalikan angka seperti bilangan bulat, lalu atur posisi desimal pada hasil akhir berdasarkan jumlah angka desimal pada bilangan yang dikalikan.
Penerapan Aritmatika pada Soal Cerita:
- Contoh: Jika seorang pekerja mendapat gaji Rp2.500.000 per bulan dan ia menyisihkan 20% untuk tabungan, berapa jumlah tabungan setelah 6 bulan?
- Strategi: Pecahkan soal ke dalam langkah-langkah kecil menggunakan operasi dasar.
Pola Deret atau Baris Bilangan

Untuk bisa menguasai soal deret angka, langkah pertama yang harus kamu lakukan adalah memahami jenis-jenis deret angka yang umum muncul dalam ujian. Deret angka pada umumnya terbagi ke dalam beberapa pola yang bisa dipelajari secara sistematis. Berikut adalah beberapa jenis deret angka yang perlu kamu ketahui.
Deret Aritmatika
Deret aritmatika adalah deret di mana setiap angka bertambah atau berkurang dengan selisih yang sama. Pola ini sangat umum ditemukan dalam soal-soal deret angka CPNS.
- Contoh Soal: 3, 6, 9, 12, …
- Jawabannya adalah 15 (selisih antar angka adalah +3).
- Tips: Temukan selisih atau penambahan konstan antara dua angka berturut-turut untuk menemukan pola.
Deret Geometri
Deret geometri adalah deret di mana setiap angka bertambah atau berkurang dengan cara dikalikan atau dibagi dengan angka tertentu.
- Contoh Soal: 2, 4, 8, 16, …
- Jawabannya adalah 32 (setiap angka dikalikan 2).
- Tips: Periksa apakah setiap angka dalam deret diperoleh dengan mengalikan atau membagi angka sebelumnya dengan suatu bilangan tetap.
Deret Kombinasi
Deret kombinasi adalah deret angka yang merupakan gabungan antara beberapa pola, seperti aritmatika dan geometri. Ini seringkali dianggap lebih sulit karena melibatkan lebih dari satu pola.
- Contoh Soal: 2, 5, 10, 17, 26, …
- Jawabannya adalah 37 (pola penambahan berurutan: +3, +5, +7, +9, +11).
- Tips: Jika pola sederhana tidak terlihat, coba analisis lebih lanjut untuk melihat apakah ada pola yang berubah secara bertahap.
Deret Bilangan Berpola Kompleks
Beberapa deret angka melibatkan pola yang lebih kompleks, seperti pengelompokan angka, penjumlahan atau pengurangan dua pola berselang-seling, atau bahkan perubahan non-linier.
- Contoh Soal: 1, 4, 9, 16, 25, …
- Jawabannya adalah 36 (bilangan kuadrat: 1², 2², 3², 4², 5², …).
- Tips: Jika angka tampak acak, periksa apakah deret tersebut mungkin merupakan hasil dari operasi matematika yang lebih kompleks seperti kuadrat, kubik, atau deret berpola khusus lainnya.
Berikut adalah beberapa variasi pola yang sering muncul :
- Pola barisan fibonacci, yaitu setiap angka selanjutnya berasal dari penjumlahan dua bilangan sebelumnya.
Contoh : 1, 2, 3, 5, 8, 13, 21, ... - Pola penjumlahan/pengurangan tetap.
Contoh : 1, 5, 9, 13, 17, 21, 25, ... (pola berikutnya bertambah 4 secara tetap) - Pola perkalian/pembagian tetap.
Contoh : 3, 6, 12, 24, 48, 98, ... (pola berikutnya dikali 2 secara tetap) - Pola bilangan ganjil.
Contoh : 11, 13, 15, 17, 19, 21, 23, ... - Pola bilangan genap
Contoh : 12, 14, 16, 18, 20, 22, 24, ... - Pola bilangan prima
Contoh : 2, 3, 5, 7, 11, 13, 17, 19, ... - Pola pangkat tetap
Contoh : 1, 4, 9, 16, 25, 36, 49, ... (pola pangkat 2 : 12, 22, 32, 42, 52, ...) - Pola loncat bilangan
Contoh : 100, 1, 90, 2, 80, 3, 70, ... (urutan ganjil berkurang sepuluh, urutan genap bertambah 1)
Perbandingan

Perbandingan adalah cara untuk membandingkan dua atau lebih nilai untuk mengetahui hubungan antar nilai tersebut. Dalam matematika, perbandingan sering digunakan untuk menyelesaikan berbagai masalah kehidupan sehari-hari, seperti kecepatan, harga, atau jarak.
Terdapat dua jenis perbandingan utama, yaitu:
Perbandingan Senilai
Perbandingan senilai adalah hubungan antara dua besaran yang meningkat atau menurun secara bersamaan. Artinya, jika salah satu besaran bertambah, maka besaran lainnya juga bertambah dengan proporsi yang sama, begitu pula jika berkurang.
Ciri-Ciri Perbandingan Senilai
- Nilai kedua besaran bertambah atau berkurang secara bersamaan.
- Rasio (perbandingan) antara dua besaran selalu konstan.
Rumus Perbandingan Senilai
Jika A dan B adalah dua besaran yang memiliki hubungan perbandingan senilai, maka:
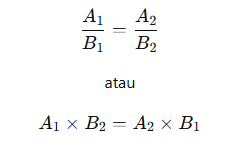
Contoh Soal
Sebuah mobil memerlukan 4 liter bensin untuk menempuh 80 km. Berapa liter bensin yang dibutuhkan untuk menempuh 200 km?
Diketahui:
- A1 = 4 liter
- B1 = 80 km
- B2 = 200 km
Gunakan rumus:
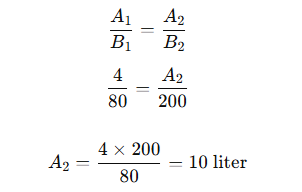
Perbandingan Berbalik Nilai
Perbandingan berbalik nilai adalah hubungan antara dua besaran di mana jika salah satu besaran bertambah, maka besaran lainnya berkurang, dan sebaliknya, dengan proporsi yang tetap.
Ciri-Ciri Perbandingan Berbalik Nilai
- Salah satu besaran bertambah, sementara yang lain berkurang.
- Hasil kali antara dua besaran selalu konstan.
Rumus Perbandingan Berbalik Nilai
Jika A dan B adalah dua besaran yang memiliki hubungan perbandingan berbalik nilai, maka:
A1 x B1 = A2 x B2
Contoh Soal
Sebuah pekerjaan dapat diselesaikan oleh 5 orang dalam waktu 12 hari. Berapa hari yang dibutuhkan jika pekerja ditambah menjadi 10 orang?
Diketahui:
- A1 = 5 orang
- B1 = 12 hari
- A2 = 10 orang
Gunakan rumus:
Data dan Penyajiannya

Data adalah kumpulan informasi yang diperoleh dari suatu pengamatan, penelitian, atau survei. Data dapat disajikan dalam bentuk tabel, diagram, atau grafik untuk memudahkan analisis.
Dalam statistik, terdapat tiga ukuran pemusatan data yang sering digunakan, yaitu:
- Mean (Rata-rata)
- Median (Nilai Tengah)
- Modus (Nilai yang Paling Sering Muncul)
Mean (Rata-rata)
Mean adalah nilai rata-rata yang dihitung dengan menjumlahkan semua data, lalu membaginya dengan jumlah data.
Rumus Mean
Untuk data tunggal:
Mean = (Jumlah seluruh data) / (Jumlah data)
Contoh Soal
- Seorang siswa memperoleh nilai: 80, 85, 90, 75, dan 95. Hitung rata-rata nilainya!
- Mean = (80 + 85 + 90 + 75 + 95)/5 = 425/5 = 85
Median (Nilai Tengah)
Median adalah nilai yang berada di tengah data setelah data diurutkan dari yang terkecil hingga terbesar. Jika jumlah data ganjil, median adalah data di posisi tengah. Jika jumlah data genap, median adalah rata-rata dari dua data tengah.
Langkah Menentukan Median
- Urutkan data dari kecil ke besar.
- Tentukan jumlah data (n):
- Jika n ganjil: Median adalah data ke-(n+1)/2 .
- Jika n genap: Median adalah rata-rata data ke-(n/2) dan ke-(n/2) + 1
Contoh Soal
- Data: 40, 35, 50, 45, 30. Tentukan mediannya!
Urutkan: 30, 35, 40, 45, 50.
n=5 (ganjil), Median = data ke-(5+1)/2 = data ke-3 = 40. - Data: 25, 20, 15, 10, 5, 30. Tentukan mediannya!
Urutkan: 5, 10, 15, 20, 25, 30.
n=6 (genap), Median = rata-rata data ke-3 dan ke-4:
Median = (15 + 20)/2 = 17,5
Modus (Nilai yang Sering Muncul)
Modus adalah nilai yang paling sering muncul dalam sekumpulan data. Sebuah data dapat memiliki:
- Satu modus (unimodal)
- Dua modus (bimodal)
- Lebih dari dua modus (multimodal)
- Tidak ada modus (jika semua nilai muncul sama seringnya)
Contoh Soal
- Data: 5, 7, 5, 9, 10, 5, 7, 10. Tentukan modusnya!
- Frekuensi:
- 5: 3 kali
- 7: 2 kali
- 9: 1 kali
- 10: 2 kali
- Modus = 5 (muncul paling sering).
- Frekuensi:
- Data: 2, 3, 3, 4, 4, 5. Tentukan modusnya!
- Frekuensi:
- 3: 2 kali
- 4: 2 kali
- Modus = 3 dan 4 (bimodal).
- Frekuensi:
1.
Jawablah soal berikut ini!
2, 5, 11, 23, 47, 95, ...
A. 105
B. 180
C. 190
D. 191
E. 200
JAWABAN BENAR
D.
191
PEMBAHASAN
Jawaban : D
2.
Jawablah soal berikut ini!
2, 3, 6, 5, 18, 7, 54, 9, …
A. 90
B. 108
C. 126
D. 144
E. 162
JAWABAN BENAR
E.
162
PEMBAHASAN
Larik : 2
Tingkat : 1
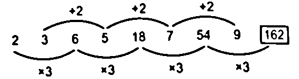
Jawaban : E
3.
Jawablah soal berikut ini!
Sebanyak 2/3 dari peserta sebuah workshop adalah laki-laki. Sebanyak 1/4 peserta perempuan belum menikah. Jika ada 9 orang peserta perempuan yang sudah berkeluarga, jumlah seluruh peserta workshop adalah ....
A. 28 orang
B. 30 orang
C. 32 orang
D. 36 orang
E. 38 orang
JAWABAN BENAR
D.
36 orang
PEMBAHASAN
L = 2/3 bagian
P = 1 - 2/3 = 1/3 bagian
P belum menikah = 1/4 P
P sudah menikah = 1 - 1/4 = 3/4 P
3/4 P = 9
P = 9 (4/3) = 12
P = 1/3 X
12 = 1/3 X
X = 36
Jawaban D
4.
Jawablah soal berikut ini!
Gaji Toni 125% dari gaji Joni, sedangkan gaji Meri hanya 80% dari gaji Joni. Jika jumlah gaji ketiganya adalah Rp 6.100.000, maka gaji Meri adalah ....
A. Rp 1.000.000
B. Rp 1.200.000
C. Rp 1.400.000
D. Rp 1.600.000
E. Rp 1.800.000
JAWABAN BENAR
D.
Rp 1.600.000
PEMBAHASAN
125% J + 100% J + 80% J = 6100
305% J = 6100
J = 100/305 x 6100 = 2000
Meri = 80% x 2000 = 1600
Jadi, gaji Meri adalah Rp 1.600.000.
Jawaban D
5.
Jawablah soal berikut ini!
Di dalam suatu ujian, masing-masing siswa diberikan skor 5, 10, atau 15. Banyaknya siswa untuk masing-masing skor ditunjukkan pada table berikut.
Jika median skornya adalah 10, maka nilai terbesar yang mungkin adalah ....
A. 8
B. 9
C. 19
D. 20
E. 21
JAWABAN BENAR
C.
19
PEMBAHASAN
Agar mediannya 10, maka nilai tengah terletak pada data ke = 8 + 12 = 20.
Jadi, banyak data disebelah kanan median atau x, haruslah sama dengan banyak data di sebelah kiri median = 8 + 11 = 19.
Jawaban C

Oops!!!
Yah, jawaban kamu meleset nih. Ingin melihat pembahasan soal ini?

BENAR!!!
Selamat!
Jawaban kamu benar. Ingin lihat pembahasan soal ini?
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved

