Daftar Materi
MATERI
Fungsi
RELASI
Sobat pintar masih ingat tidak apa itu relasi?
Relasi menyatakan hubungan antara anggota himpunan dengan anggota himpunan lain. Himpunan A dan Himpunan B dikatakan memiliki relasi jika terdapat anggota himpunan yang saling berpasangan dengan hubungan tertentu
Relasi antara dua himpunan dapat dinyatakan dengan tiga cara yaitu:
a) Diagram Panah
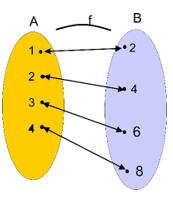
b) Himpunan Pasangan Berurutan
K = {(1,2),(2,4),(3,6),(4,8),(5,10)
c) Diagram Kartesius
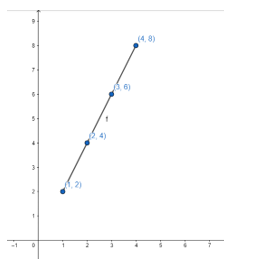
FUNGSI
Fungsi (pemetaan) adalah relasi dari himpunan A ke himpunan B, jika terdapat setiap anggota berpasangan tepat satu anggota himpunan B. Semua anggota himpunan A disebut domain (daerah asal), semua anggota himpunan B disebut kodomain (daerah kawan) dan hasil dari pemetaan himpunan A dan himpunan B adalah daerah hasil (range). Sama seperti relasi, fungsi juga dapat dinyatakan dalam bentuk diagram panah, diagram kartesius, dan himpunan pasangan berurutan
Suatu fungsi secara sistematis dapat dituliskan:
f:x -> ax+b (fungsi f memetakan x ke ax+b)
atau
f(x) = ax+b (fungsi dalam x)
atau
y= ax+b (y adalah fungsi dari x)
Catatan
Jika f(x)=y, maka y merupakan bayangan x (image), sedangkan x merupakan prabayangan dari y (pra-image)
Fungsi dapat disajikan dalam bentuk:
- diagram panah
- diagram cartesius
- himpunan pasangan berurutan
DOMAIN, KODOMAIN DAN RANGE FUNGSI
Jika f adalah suatu fungsi dari A ke B, maka himpunan A disebut domain (daerah asal) dan himpunan B disebut kodomain (daerah kawan). Sedangkan himpunan B yang berpasangan (himpunan C) disebut range (hasil) fungsi f.
Aturan yang memasangkan anggota himpunan A dengan anggota-anggota himpunan B disebut aturan fungsi f.
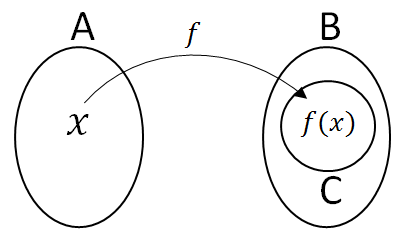
Domain suatu fungsi dapat ditetapkan secara jelas (eksplisit). Jika domain tidak ditetakan dengan jelas, maka digunakan kesepakatan bahwa domainnya merupakan himpunan bilangan real.
Syarat yang harus dipenuhi agar suatu fungsi terdefinisi (memiliki daerah hasil di himpunan bilangan real), yaitu:
- fungsi dalam akar
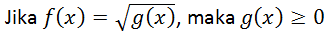
- fungsi pecahan
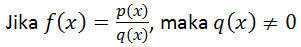
- fungsi pecahan, dimana penyebutnya merupakan fungsi lain dalam bentuk akar
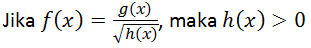
- fungsi logaritma
Jika f(x) = g(x) log h(x), maka h(x)>0, g(x)>0 dan g(x) tidak sama dengan 1
GRAFIK FUNGSI
Suatu fungsi dari himpunan A ke himpunan B dapat dbuat grafik pemetaannya dengan menggunakan diagram cartesius. Grafik suatu fungsi dapat berupa garis lurus maupun kurva.
Langkah-langkah menggambar grafik fungsi pada koordinat cartesius, yaitu:
- Tentukan domain (jika belum diketahui secara pasti, pilih beberapa bilangan bulat disekitar nol)
- Tentukan pasangan berurutan dari fungsi tersebut
- Gambar pasangan berurutan sebagai titik pada koordinat cartesius
- Hubungkan titik-titik yang sudah digambar pada koordinat cartesius
Berdasarkan grafik suatu fungsi, dapat ditentukan domain dan range nya. Domain fungsi terletak pada sumbu x, sedangkan kodomain fungsi terletak pada sumbu y.
OPERASI ALJABAR FUNGSI
Pada dua atau lebih fungsi dapat dilakukan operasi aljabar seperti penjumlahan, pengurangan, perkalian dan pembagian.
Operasi aljabar yang berlaku pada fungsi, antara lain:
SPLDV dan SPLTV
SISTEM PERSAMAAN LINEAR DUA VARIABEL (SPLDV)
Sistem persamaan adalah himpunan persamaan yang saling berhubungan. Variabel merupakan nilai yang dapat berubah-ubah. Persamaan linear adalah suatu persamaan yang memiliki variabel dengan pangkat tertingginya adalah 1 (satu). Sistem persamaan linear Dua Variabel (SPLDV) merupakan suatu sistem yang terdiri atas dua persamaan linier yang mempunyai dua variabel. Dalam sebuah Sistem Persamaan Linear Dua Variable (SPLDV) biasanya melibatkan dua persamaan dengan dua variabel.
Contoh SPLDV:
2x + 5y = 14
3a + 4b = 24
q + r = 3
Bentuk umum sistem persamaan linier dua variabel (SPLDV) dengan variabel x dan y serta a, b, c, d, e, f bilangan real :
ax + by = c
dx + ey = f
SISTEM PERSAMAAN LINEAR TIGA VARIABEL
Sistem persamaan linear tiga variabel (SPLTV) yaitu juga merupakan bentuk perluasan dari sistem persamaan linear dua variabel (SPLDV)
Bentuk umum dari Sistem Persamaan Linear Tiga Variabel (SPLTV) dalam x, y, dan z dapat dituliskan berikut ini :
ax + by + cz = d
ex + fy + gz = h
ix + jy + kz = l
dengan a, b, c, d, e, f, g, h, i, j, k, l merupakan bilangan real
MENYELESAIKAN SPLDV DAN SPLTV
Untuk menyelesaikan SPLDV dan SPLTV dapat dilakukan dengan cara yang sama, yaitu eliminasi, substitusi, dan campuran. Hanya saja SPLTV proses menentukan nilai variabelnya lebih lama karena variabelnya lebih banyak.
Metode Eliminasi
Langkah-langkah menyelesaikan SPLDV dengan metode eliminasi:
1. Menyamakan salah satu koefisien dari variabel x atau y dari kedua persamaan dengan cara mengalikan konstanta yang sesuai.
2. Hilangkan variabel yang memiliki koefisien yang sama dengan cara menambahkan atau mengurangkan kedua persamaan.
3. Ulangi kedua langkah untuk mendapatkan varibel yang belum diketahui.
4. Penyelesaiannya adalah (x, y).
Metode Substitusi
Langkah-langkah menyelesaikan SPLDV dengan metode eliminasi:
1. Menyamakan salah satu koefisien dari variabel x atau y dari kedua persamaan dengan cara mengalikan konstanta yang sesuai.
2. Hilangkan variabel yang memiliki koefisien yang sama dengan cara menambahkan atau mengurangkan kedua persamaan.
3. Ulangi kedua langkah untuk mendapatkan varibel yang belum diketahui.
4. Penyelesaiannya adalah (x, y).
Metode Campuran
Metode campuran berarti gabungan dari metode eliminasi dan substitusi tanpa ditentukan urutannya.
Pertidaksamaan dan Program Linear
Pertidaksamaan Linear Dua Variabel
Pertidaksamaan Linear Dua Variabel merupakan suatu pertidaksamaan yang memuat dua variabel dengan masing-masing variabel berderajat satu dan dihubungkan dengan tanda ketidaksamaan.
Bentuk umum Pertidaksamaan Linear Dua Variabel
Bentuk umum dari pertidaksamaan Linear Dua Variabel antara lain:
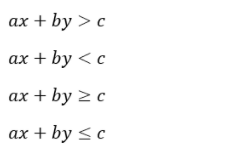
Contoh bentuk sistem pertidaksamaan linear dua variabel :
Langkah-langkah Penyelesaian Sistem Pertidaksamaan Linear Dua Variabel
Penyelesaian dari sistem pertidaksamaan linear dua variabel berupa daerah penyelesaian, baik berupa daerah yang diarsir maupun daerah yang bersih. Untuk menentukan daerah penyelesaiannya, langkah-langkah yang dilakukan yaitu:
- Ubah tanda ketaksamaan menjadi persamaan, sehingga diperoleh persamaan linear dua variabel
- Lukis grafik dari persamaan linear yang diperoleh dengan menentukan titik potong sumbu x dan sumbu y dari persamaan linear
- Uji titik yang berada di sebelah kanan atau kiri garis, kemudian substitusi titik koordinat (x,y) pada pertidaksamaan sehigga menghasilkan pernyataan
- Jika pernyataan yang dihasilkan benar, maka daerah tersebut merupakan penyelesaiannya. Jika pernyataan salah, maka daerah yang tidak memuat titik tersebut merupakan daerah penyelesaiannya
Pertidaksamaan Kuadrat Dua Variabel
Pertidaksamaan kuadrat dua variabel merupakan suatu pertidaksamaan yang memuat dua variabel dengan salah satu atau kedua variabel maksimal berderajat dua dan dihubungkan dengan tanda ketidaksamaan. Perbedaan pertidaksamaan linear dengan pertidaksamaan kuadrat adalah pada derajat (pangkat) variabelnya.
Bentuk umum Pertidaksamaan Kuadrat Dua Variabel
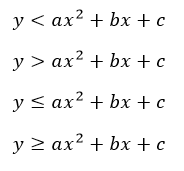
Contoh bentuk sistem pertidaksamaan linear dua variabel :
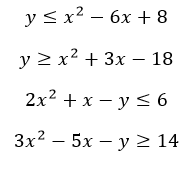
Langkah-langkah Penyelesaian Sistem Pertidaksamaan Kuadrat Dua Variabel
Penyelesaian dari sistem pertidaksamaan kuadrat dua variabel berupa daerah penyelesaian, baik berupa daerah yang diarsir maupun daerah yang bersih. Untuk menentukan daerah penyelesaiannya, langkah-langkah yang dilakukan yaitu
- Tentukan arah kurva terbuka ke atas atau ke bawah di lihat dari koefisien x kuadrat
- Sketsa gambar dengan menentukan titik potong dengan sumbu x
- Tetapkan interval yang memenuhi y > 0, berarti grafik terletak di atas sumbu x, y < 0 berarti terletak di bawah sumbu x
- Tentukan titik puncak dari kurva
Program Linear
Masalah program linear dua variabel adalah menentukan nilai x,y yang mengoptimumkan (maksimum atau minimum) fungsi tujuan Z(x,y)=C1 x+C2 y dengan kendala:
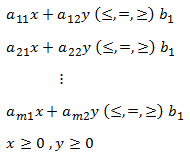
Langkah-langkah dalam membuat model matematika dari kendala yang ada yaitu :
- Tuliskan kendala pada soal dengan bantuan tabel
- Tentukan besaran masalah sebagai variabel yang akan digunakan
- Buatlah Sistem Pertidaksamaan Linear Dua Variabel berdasarkan kendala pada tabel
- Tentukan fungsi tujuan sebagai fungsi yang akan menjadi nilai optimum
Setelah membuat model matematika berdasarkan informasi yang tersedia pada soal, kita dapat menentukan nilai optimum suatu fungsi tujuan dengan menggambarkan grafik daerah penyelesaian. Daerah penyelesaian masalah program linear merupakan himpunan semua titik (x,y) yang memenuhi kendala suatu masalah program linear. Kemudian menentukan nilai optimumnya dengan metode uji titik sudut dan metode garis selidik.
Metode Uji Titik Sudut
Menentukan nilai optimum dari fungsi tujuan dengan metode uji titik sudut menggunakan langkah-langkah berikut:
- Setelah menggambar grafik daerah penyelesaian, tentukan koordinat titik sudut dari daerah penyelesaian.
- Hitung nilai fungsi tujuan pada masing-masing titik sudut
- Nilai optimum dapat terlihat dengan membandingkan nilai-nilai fungsi tujuan pada setiap titik sudut
Metode Garis Selidik
Menentukan nilai optimum dari fungsi tujuan dengan metode garis selidik menggunakan langkah-langkah berikut:
- Setelah menggambar grafik daerah penyelesaian, lukis garis selidik ax+by=k, dengan k dapat diperbesar maupun diperkecil dan selidiki nilainya pada masing-masing titik sudut.
- Nilai optimum dicari dengan membandingkan nilai-nilai pada langkah sebelumnya
1.
Kerjakan soal berikut ini dengan tepat!
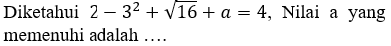
A. -7
B. -3
C. 1
D. 4
E. 7
JAWABAN BENAR
E.
7
PEMBAHASAN
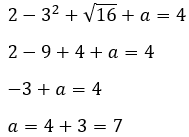
2.
Kerjakan soal berikut ini dengan tepat!
A. 11
B. 5
C. -5
D. -7
E. -11
JAWABAN BENAR
A.
11
PEMBAHASAN
3.
Kerjakan soal berikut ini dengan tepat!
Nilai x yang memenuhi x2 – 8x > 20 yaitu ….
A. x < 2
B. x > -10
C. x < -2 atau x > 10
D. -10 < x < 2
E. -2 < x < 10
JAWABAN BENAR
C.
x < -2 atau x > 10
PEMBAHASAN
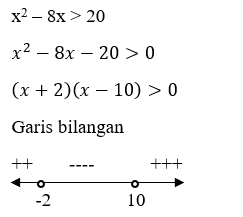
Jadi, penyelesaiannya yaitu x < -2 atau x > 10
4.
Kerjakan soal berikut ini dengan tepat!
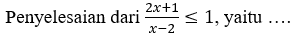
A.
B.
C.
D.
E.
JAWABAN BENAR
B.
PEMBAHASAN
5.
Perhatikan grafik berikut!
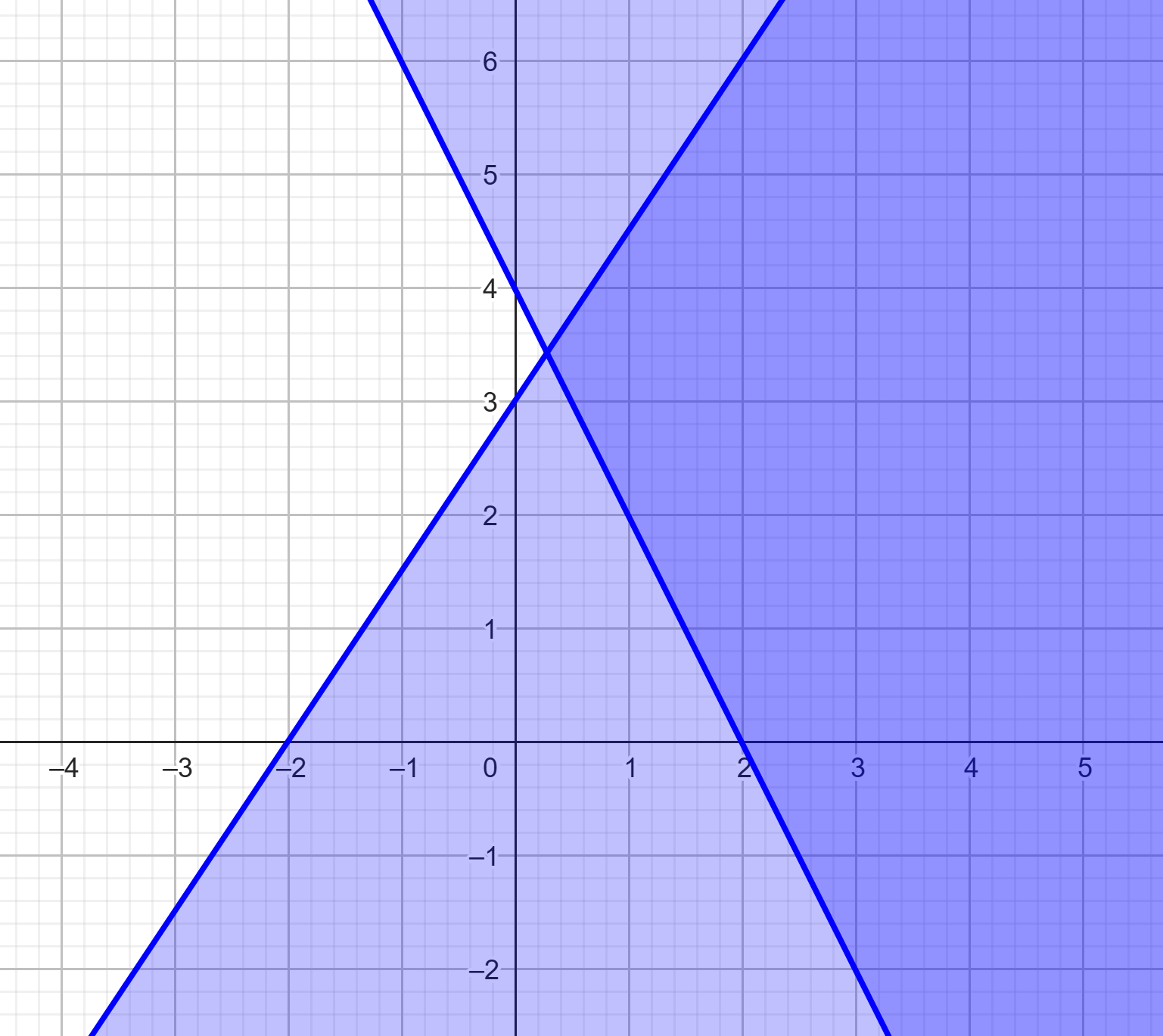
Sistem pertidaksamaan yang menunjukkan daerah penyelesaian yang diarsir pada grafik di atas, yaitu ….
A.
B.
C.
D.
E.
JAWABAN BENAR
D.
PEMBAHASAN
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
Ikuti Kami
Download Aku Pintar
