Belajar Pintar Materi SMP, SMA, SMK
BelajarPintarV3
UTBK - SNBT
Pengetahuan Kuantitatif
MATERI
Titik dan Garis


Sumber : AnakTeknik
Pernahkah kalian melihat burung yang bertengger pada kabel listrik? Kalau seandainya burung itu kita andaikan sebagai titik, kabel listrik sebagai garis, dan daratan sebagai bidang, maka kedudukan dari titik akan berubah-ubah bukan? Seperti burung yang bisa terbang, bertengger di kabel listrik maupun turun ke daratan. Nah! Kali ini, kita akan belajar bersama mengenai kedudukan titik, garis, dan bidang.
Halo, Sobat Pintar!! Pasti kalian tidak asing lagi dengan titik.
Titik yaitu suatu noktah yang hanya ditentukan letaknya, dan tidak mempunyai ukuran. Biasanya ditandai dengan huruf kapital, misalnya titik A, titik B, titik P, titik Q, dan seterusnya.
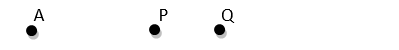
Kedudukan Titik terhadap Titik

Titik A terpisah dengan titik B, jadi titik A dan B adalah dua titik yang berbeda. Sedangkan titik B berimpit dengan titik C sehingga titik B = titik C.
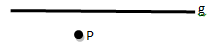
Kedudukan Titik terhadap Garis
- Sebuah titik P dikatakan terletak pada garis g, jika garis g melalui titik P.

- Sebuah titik P dikatakan diluar garis g, jika garis g tidak melalui titik P.
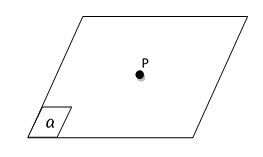
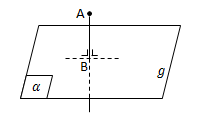
Kedudukan Titik terhadap Bidang
- Sebuah titik P dikatakan terletak pada bidang a, jika bidang a melalui titik P
- Sebuah titik P dikatakan diluar bidang a, jika bidang a tidak melalui titik P
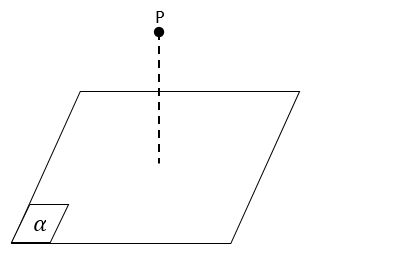
Gimana nih Sobat materi sebelumnya? Mudah bukan? Yuk kita beralih ke materi kedudukan garis!
Pada kedudukan garis ini terbagi menjadi dua sebagai berikut.
Kedudukan Dua Garis
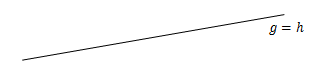
- Garis g dan garis h dikatakan berimpit jika setiap titik pada garis g juga terletak pada garis h, dan sebaliknya.
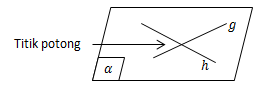
- Garis g dan garis h dikatakan saling berpotongan jika kedua garis tersebut memiliki satu titik persekutuan yang disebut titik potong. Dua garis hanya dapat berpotongan jika terletak pada suatu bidang yang sama.
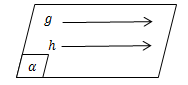
- Garis g dan garis h dikatakan sejajar jika kedua garis tidak memiliki titik persekutuan.
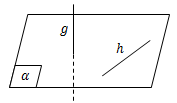
- Garis g dan garis h di katakan bersilangan jika kedua garis tidak memiliki titik persekutuan, tidak sejajar dan tidak terletak pada satu bidang yang sama.
Kedudukan Garis dan Bidang
- Garis g dikatakan terletak pada bidang a jika paling sedikit dua titik pada garis g terletak pada bidang a
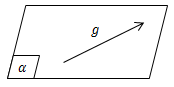
- Garis g dikatakan sejajar bidang a jika garis g sejajar dengan garis pada bidang a
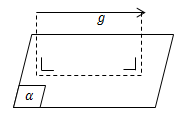
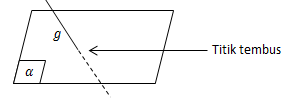
- Garis g dikatakan menembus bidang a jika garis g tidak terletak pada bidang dan tidak sejajar bidang a. Dalam hal ini, garis g dan bidang a mempunyai satu titik persekutuan yang dinamakan titik tembus.
Jarak

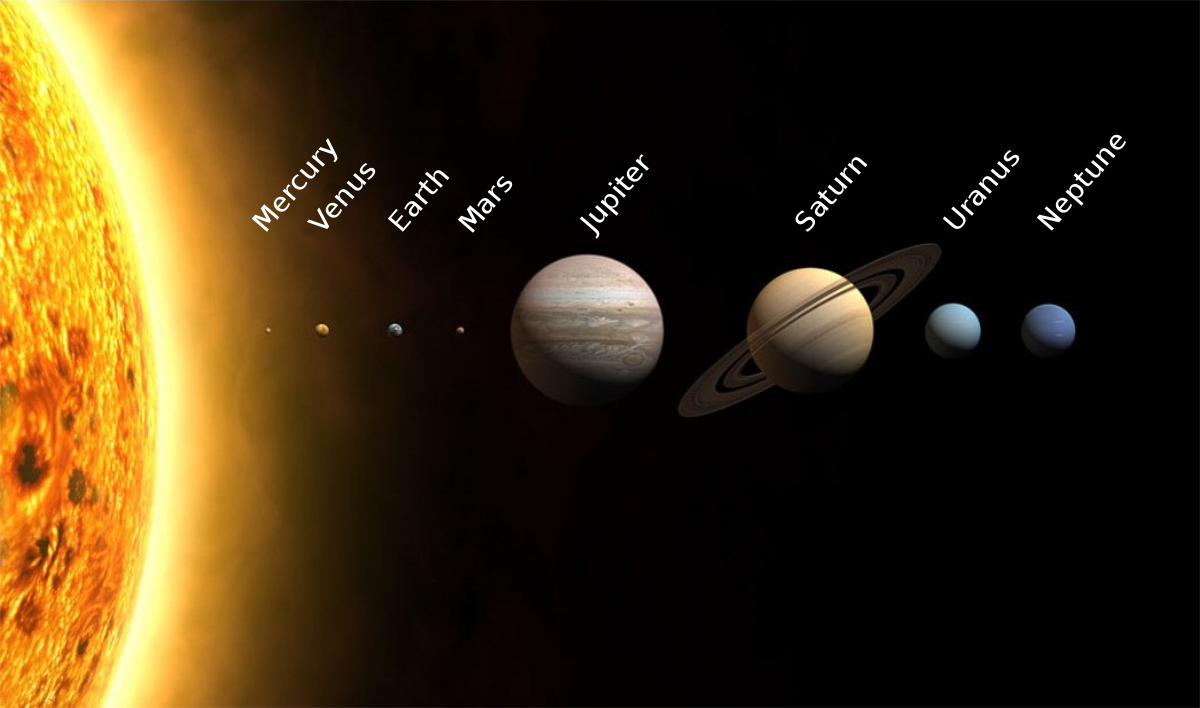
Sumber : Wikipedia.org
Pernahkah kalian berpikir berapa jarak antara planet yang satu dengan yang lainnya? Kalau kita anggap planet-planet ini sebagai titik, berapa jarak antar titik-titik tersebut?
Nah Sobat Pintar, setelah kita mempelajari tentang kedudukan titik, garis, dan bidang, kita akan mempelajari tentang jarak titik, garis, dan bidang.
Terlebih dahulu kita akan mempelajari jarak antar dua titik. Jarak titik A ke titik B sama dengan panjang ruas garis AB, yang ditentukan dengan teorema Pythagoras, yaitu:
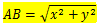
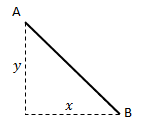
Selanjutnya adalah jarak titik ke garis. Jarak titik ke garis ini terbagi menjadi 2 yaitu:
Titik dan Garis Terletak pada Satu Bidang
Titik A dan garis g terletak pada bidang a. Untuk menentukan jarak titik A ke garis g yaitu:
- Buatlah garis h yang melalui titik A dan memotong tegak lurus garis g di B
- Titik B adalah proyek titik A pada garis g. AB adalah jarak antara titik A dan garis g.
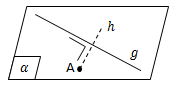
Titik dan Garis Tidak Terletak pada Satu Bidang
Garis g terletak pada bidang a. Untuk menentukan jarak antara titik A dan garis g, yaitu :
- Buatlah garis AB yang tegak lurus bidang a.
- Buatlah garis BC yang tegak lurus garis g.
- AC adalah jarak antara titik A dan garis g.
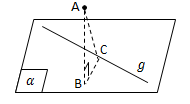
Terakhir yaitu jarak antar titik ke bidang. Titik A terletak di luar bidang a. Untuk menentukan jarak antara titik A dan bidang a adalah sebagai berikut.
- Buatlah garis g yang melalui titik A dan tegak lurus bidang a.
- Jika garis g menembus bidang di B, maka AB adalah jarak antara titik A dan bidang a.
Sudut

Secara matematis, hubungan sinar garis dan titik sudut diilustrasikan sebagai berikut.
Gambar Sudut yang terbentuk oleh dua sinar garis
Suatu sudut terbentuk dari perpotongan dua sinar garis yang berpotongan tepat di satu titik, sehingga titik potongnya disebut dengan titik sudut.
Nama suatu sudut dapat berupa simbol alfa, beta, dll, atau berdasarkan titik titik yang melalui garis yang berpotongan tersebut. Biasanya, satuan sudut dinyatakan dalam dua jenis, yaitu derajat (o) dan radian (rad). Sudut APB bisa juga disebut Sudut P, dan besar sudut P dilambangkan dengan m sudut P.
Keterangan: Besar sudut satu putaran penuh adalah 360o
PENAMAAN SUDUT
Secara matematis, penamaan sudut diperlukan untuk mempermudah penamaan sudut untuk kajian selanjutnya. Mari kita perhatikan Gambar berikut ini.
Gambar Penamaan Sudut ABC atau Sudut CBA
Dari Gambar tersebut BA dan BC disebut kaki sudut. Titik B adalah titik sudut. Secara umum, ada dua penamaan sudut, yaitu:
- Titik B dapat dikatakan sebagai titik sudut B seperti pada Gambar di atas. Ingat, penulisannya selalu menggunakan huruf kapital.
- Sudut yang terbentuk pada gambar di samping dapat juga disimbolkan dengan sudut ABC atau sudut CBA atau sudut B.
Pada setiap sudut yang terbentuk, harus kita tahu berapa besar derajat sudutnya. Secara manual, kita dapat menggunakan alat ukur sudut yaitu busur. Alat ini dapat membantu kita mengukur suatu sudut yang sudah terbentuk dan membentuk besar sudut yang akan digambar.
Gambar Busur, alat untuk mengukur sudut
Perlu kita kenalkan bahwa, terdapat ukuran sudut standar yang perlu kita ketahui, seperti yang disajikan pada gambar di bawah ini
Gambar Sudut lancip, tumpul, siku-siku, dan sudut lurus
Jenis-Jenis Sudut
- Sudut Siku-Siku: ukuran sudutnya 90o
- Sudut Lancip: ukuran sudutnya antara 0o dan 90o
- Sudut Tumpul: ukuran sudutnya antara 90o dan 180o
- Sudut Lurus: ukuran sudutnya 180o
- Sudut Reflek: ukuran sudutnya antara 180o dan 360o
JENIS-JENIS SUDUT
1. Sudut berpelurus
Sudut berpelurus adalah sudut yang apabila dijumlahkan keduanya bernilai 180o.
Berpelurus diambil dari kata dasar lurus yang dibentuk oleh sebuah garis lurus adalah 180o. Dua sudut yang disebut saling berpelurus adalah apabila jumlah besar kedua sudut tersebut adalah 180o. Sudut yang satu disebut pelurus dari sudut yang lain.
Dengan demikian misalkan Sudut ABD dan Sudut CBD saling berpelurus, maka Sudut ABD + Sudut CBD = 180o. Untuk lebih jelasnya perhatikan gambar dibawah ini
2. Sudut berpenyiku
Sudut berpenyiku adalah sudut yang apabila dijumlahkan keduanya bernilai 90o.
Sesuai dengan judul berpenyiku dengan kata dasar siku atau siku-siku maka besar sudutnya adalah 90o. Apabila dua sudut yang letaknya saling bersebelahan membentuk sudut siku-siku atau jumlah besar sudutnya 90o maka sudut-sudut tersebut dapat dikatakan saling berpenyiku atau disebut juga komplemen. Sudut yang satu disebut penyiku dari sudut yang lain.
Dengan demikian misalkan Sudut ADB dan Sudut BDC saling berpenyiku, maka Sudut ADB + Sudut BDC merupakan penyiku dari Sudut ABC. Perhatikan gambar dibawah ini!
Sudut yang saling bertolak belakang merupakan sudut yang posisinya saling bertolak belakang atau sudut yang membelakangi dan tentunya sama besar. Perhatikan gambar dibawah ini.
Sudut A = Sudut C (bertolak belakang)
Sudut B = Sudut D (bertolak belakang)
Sudut E = Sudut G (bertolak belakang)
Sudut F = Sudut H (bertolak belakang)
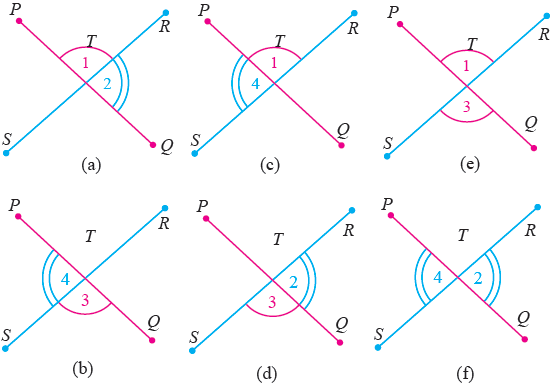
Gambar Sudut berpelurus dan bertolak belakang
- Pada gambar (a) dan (b) termasuk sudut berpelurus, yaitu m Sudut T1 + m Sudut T2 = 180o dan m Sudut T3 + m Sudut T4 = 180o
- Pada gambar (c) dan (d) juga termasuk sudut berpelurus yaitu mT1 Sudut + m Sudut T4 = 180o dan m Sudut T2 + m Sudut T3 = 180o
- Pada gambar (e) dan (f) termasuk sudut sudut bertolak belakang, m Sudut T1 = m Sudut T3 dan m Sudut T2 = m Sudut T4
Perhatikan contoh soal dibawah ini
Contoh Soal :
Perhatikan gambar berikut. Tentukan nilai ao dan bo
Gambar Pasangan sudut-sudut bertolak belakang
Penyelesaian :
Untuk menyelesaikan soal ini, kita harus memahami sudut pelurus dan memahami pasangan sudut yang saling bertolak belakang. Pasangan-pasangan sudut bertolak belakang dari Gambar sebagai berikut.
- a + 60 sama dengan 180 (sudut pelurus)
a + 60 = 180
a = 180 – 60
a = 120o
- 60 sama besar dengan b (bertolak belakang)
60 = b
b = 60o
- a sama besar dengan c (bertolak belakang)
a = c
120 = c (sudah ditemukan a =120o)
c = 120o
Jadi nilai a = 120o, b = 60odan c = 120o
HUBUNGAN SUDUT DENGAN GARIS
Coba perhatikan Gambar berikut, yakni gambar lintasan kereta api dan modelnya.
Dua garis berwarna hijau, merupakan dua segmen garis sejajar, kita sebut garis k dan garis l, dipotong oleh garis garis m pada Gambar diatas sehingga membentuk delapan sudut.
Kedelapan sudut dapat digambarkan seperti gambar berikut.
Gambar Garis k dan l merupakan dua garis sejajar dipotongan oleh satu garis m
Perhatikan contoh soal dibawah ini
Contoh Soal :
Perhatikan gambar dibawah ini. Tentukan nilai x-nya
Penyelesaian :
Coba ingat kembali tentang materi sudut yang saling bertolak belakang pada bagian Masalah di atas, yakni sebagai berikut
Karena garis k//l, akibatnya besar sudut 3x dengan besar sudut 60o membetuk sudut berpelurus
3x + 60 = 180 berpelurus
3x = 180 - 60
3x = 120
x = 40
Jadi nilai x = 40o
Bangun Datar
Bangun Datar merupakan objek geometri dua dimensi (2D) yang dibatasi oleh garis-garis lurus atau lengkung, dan hanya memiliki ukuran panjang dan lebar. Bangun datar tidak memiliki tinggi dan tebal, sehingga hanya memiliki luas dan keliling.
Bangun datar memiliki ciri-ciri umum, yaitu: Terbentuk dari garis-garis yang saling berhubungan, Memiliki luas dan keliling, Tidak memiliki ketebalan atau ketinggian.
Contoh bangun datar, yaitu : segitiga, persegi, persegi panjang, trapesium, belah ketupat, layang-layang, jajargenjang, dan lingkaran
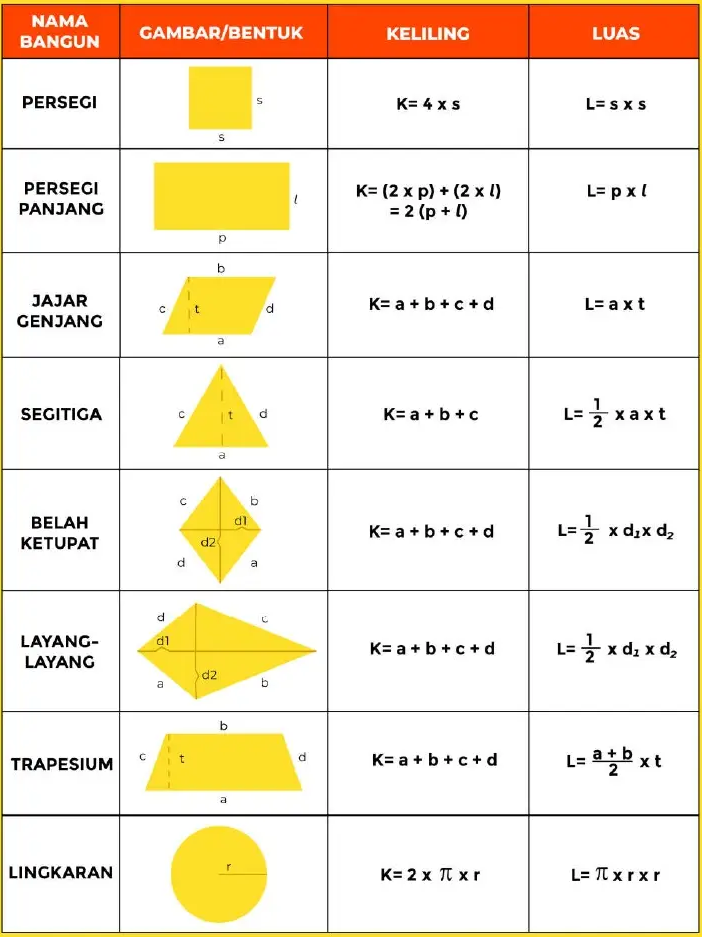
Berikut ini rumus keliling dan luas bangun datar
Bangun Ruang

Bangun Ruang terbagi menjadi 2 jenis, yaitu bangun ruang sisi datar (kubus, balok, limas, dan prisma) serta bangun ruang sisi lengkung (tabung, kerucut, bola)
BANGUN RUANG SISI DATAR
Kubus
kubus adalah bangun ruang yang dibatasi oleh 6 buah sisi yang berbentuk persegi (bujur sangkar). Beberapa orang sering menyebut bangun ini sebagai bidang enam beraturan dan juga prisma segiempat dengan tinggi sama dengan sisi alas.
Rumus-rumus Kubus
Volume = s x s x s = s3
Luas Permukaan = 6 x s x s = 6 s2
Balok
Balok adalah bangun ruang yang memiliki tiga pasang sisi segi empat (total 6 buah) dimana sisi-sisi yang berhadapan memiliki bentuk dan ukuran yang sama. Berbeda dengan kubus yang semua sisinya berbentuk persegi yang sama besar, balok sisi yang sama besar hanya sisi yang berhadapan dan tidak semuanya berbentuk persegi, kebanyakan bentuknya persegi panjang.
Rumus-rumus Balok
Volume = panjang x lebar x tinggi = p x l x t
Luas Permukaan = 2 (pl + pt + l t)
Limas
Limas adalah bangun ruang dengan alas berbentuk segi banyak, bisa segi tiga, segi empat, segi lima, dll dan bidang sisi tegaknya berbentuk segitiga yang berpotongan pada satu titik puncak. Ada banyak macam bangun ruang limas. Penamaannya berdasarkan bentuk alasnya.
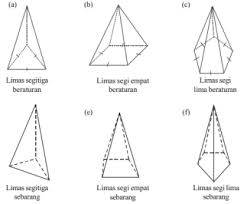
Rumus-rumus Limas
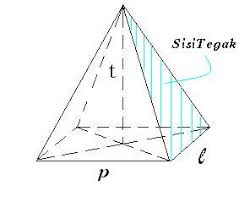
Volume = 1/3 x Luas alas x Tinggi
Luas Permukaan = Jumlah Luas alas + Jumlah Luas sisi tegak
Prisma
Prisma memiliki bidang alas dan bidang atas yang sejajar dan kongruen. Sisi lainnya berupa sisi tegak berbentuk pesegi panjang yang tegak lurus ataupun titik dengan bidang alas dan bidang atasnya. Jika dilhat dari bentuk alasnya ada yang namanya prisma segitiga, prisma segi empat, prisma segi lima, dan seterusnya. Jika alasnya berbentuk segi n Sobat Pintar bisa memberikan nama prisma segi n.
Rumus-rumus Prisma
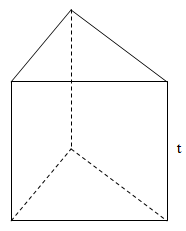
Volume = Luas alas x Tinggi
Luas permukaan = (2 x Luas Alas) + (Keliling alas x tinggi)
BANGUN RUANG SISI LENGKUNG
Kerucut
kerucut adalah sebuah limas istimewa yang beralas lingkaran. Kerucut memiliki 2 sisi dan 1 rusuk.
Rumus Kerucut:
1. Luas Alas
![]()
2. Luas Selimut
3. Luas Permukaan
4. Volume
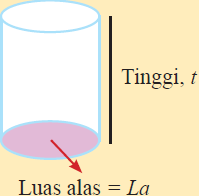
Tabung
Tabung adalah bangun ruang sisi lengkung yang dibentuk oleh dua buah lingkaran identik yang sejajar dan sebuah persegi panjang yang mengelilingi kedua lingkarn tersebut. Tabung memiliki tiga sisi yakni dua sisi datar dan satu sisi lengkung.
Luas permukaan tabung ekuivalen dengan jumlahan semua luas bangun penyusun dari jaring-jaring tabung. Jaring-jaring tabung terdiri atas dua lingkaran dan satu persegi panjang.

Volume tabung
Bola
Bola adalah bangun ruang sisi lengkung yang dibatasi oleh satu bidang lengkung. Bola didapatkan dari bangun setengah lingkaran yang diputar satu putaran penuh atau 360 derajat pada garis tengahnya.
Rumus Luas Permukaan Bola

Rumus Volume Bola

1.
Kerjakan soal berikut ini!
Sebuah tabung dengan tutup yang berjari-jari 14 cm memiliki luas permukaan 2.992 cm2. Jika sebuah kerucut dengan jari-jari dan tinggi yang sama dimasukkan ke dalam tabung tersebut, berapa volume sisa volume tabung diluar kerucut?
A. 20 cm3
B. 1760 cm3
C. 4107 cm3
D. 8213 cm3
E. 12320 cm3
JAWABAN BENAR
D.
8213 cm3
PEMBAHASAN
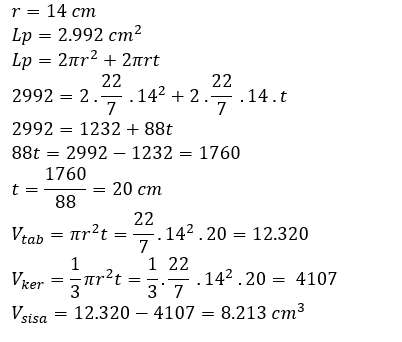
2.
Kerjakan soal berikut ini!
Diketahui kubus ABCD.EFGH dengan panjang rusuk 8cm. Titik P dan Q berturut-turut adalah titik tengah dari garis BC dan CD. Volume limas APQ.E yaitu ….
A.

B.

C.

D.

E.

JAWABAN BENAR
E.

PEMBAHASAN
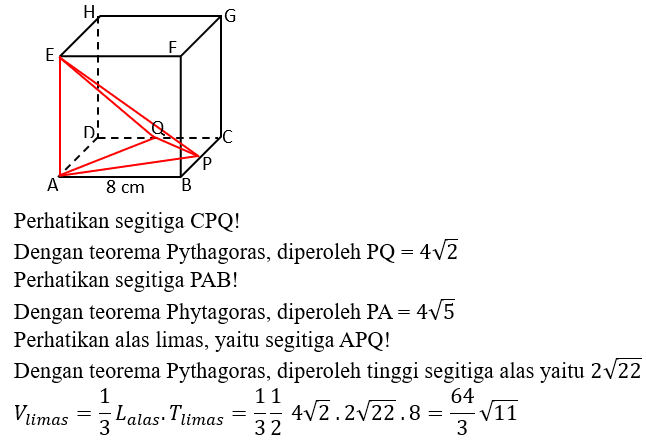
3.
Perhatikan bangun berikut ini!
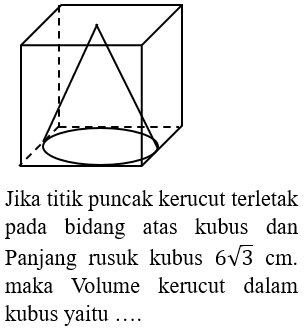
A.

B.

C.

D.

E.

JAWABAN BENAR
E.

PEMBAHASAN

4.
Kerjakan soal berikut ini!
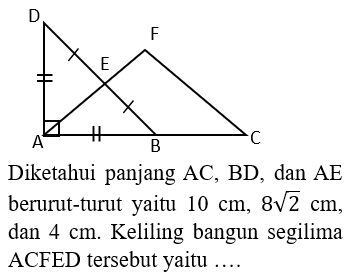
A.

B.

C.

D.

E.

JAWABAN BENAR
B.

PEMBAHASAN

5.
Kerjakan soal berikut ini!
Diketahui sebuah balok dengan perbandingan panjang, lebar, dan tinggi berturut-turut adalah 1 : 2 : 3 memiliki luas permukaan 198 cm2. Jika sebuah kubus akan dimasukkan ke dalam balok, maka rusuk kubus berikut agar kubus dapat muat dalam balok adalah ….
A. 2 cm
B. 4 cm
C. 6 cm
D. 8 cm
E. 9 cm
JAWABAN BENAR
A.
2 cm
PEMBAHASAN


Oops!!!
Yah, jawaban kamu meleset nih. Ingin melihat pembahasan soal ini?

BENAR!!!
Selamat!
Jawaban kamu benar. Ingin lihat pembahasan soal ini?
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved

