Belajar Pintar Materi SMP, SMA, SMK
BelajarPintarV3
UTBK - SNBT
Pengetahuan Kuantitatif
MATERI
Himpunan dan Jenis Himpunan

Kelompok, kumpulan, kelas, maupun gerombolan dalam matematika dikenal dengan istilah himpunan. Namun, tidak semua kumpulan termasuk himpunan.
Kumpulan yang termasuk himpunan
- Kumpulan siswa yang lahir pada bulan Agustus
- Kumpulan siswa laki-laki
- Kumpulan buah-buahan yang diawali dengan huruf M
- Kumpulan nama kota di Indonesia yang diawali dengan huruf S
- Kumpulan binatang yang berkaki dua
- Kumpulan negara di Asia Tenggara
Kumpulan yang termasuk bukan himpunan
- Kumpulan kota-kota besar di Indonesia
- Kumpulan orang kaya di Indonesia
- Kumpulan siswa yang pandai di sekolahmu
- Kumpulan gunung yang tinggi di Indonesia
- Kumpulan pelajaran yang disenangi siswa
- Kumpulan makanan yang lezat
Dari contoh diatas maka bisa diambil kesimpulan bahwa yang termasuk Himpunan adalah kumpulan yang bisa diukur dan definisikan sama oleh semua orang.
Penyajian Himpunan
Sekarang kita lanjut memahami tentang penyajian himpunan.
Cara 1: Dinyatakan dengan menyebutkan anggotanya (enumerasi)
Suatu himpunan dapat dinyatakan dengan menyebutkan semua anggotanya yang dituliskan dalam kurung kurawal. Manakala banyak anggotanya sangat banyak, cara mendaftarkan ini biasanya dimodifikasi, yaitu diberi tanda tiga titik ("…") dengan pengertian “dan seterusnya mengikuti pola"
Cara 2: Dinyatakan dengan menuliskan sifat yang dimiliki anggotanya
Suatu himpunan dapat dinyatakan dengan menyebutkan sifat yang dimiliki anggotanya.
Cara 3: Dinyatakan dengan notasi pembentuk himpunan
Suatu himpunan dapat dinyatakan dengan menuliskan syarat keanggotaan himpunan tersebut.
DIAGRAM VENN
Petunjuk dalam membuat diagram Venn antara lain:
- Himpunan semesta (S) digambarkan sebagai persegi panjang dan huruf S diletakkan di sudut kiri atas.
- Setiap himpunan yang ada dalam himpunan semesta ditunjukkan oleh kurva tertutup sederhana.
- Setiap anggota himpunan ditunjukkan dengan titik.
- Bila anggota suatu himpunan mempunyai banyak anggota, maka anggotaanggotanya tidak perlu dituliskan.
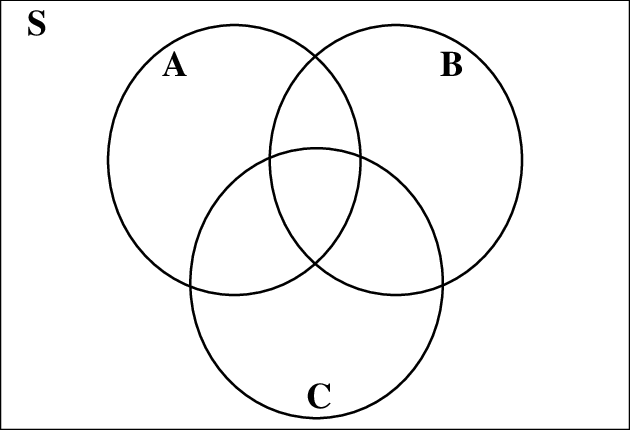
JENIS JENIS HIMPUNAN
Himpunan terbagi menjadi beberapa macam yaitu :
- Himpunan Semesta, himpunan yang anggotanya adalah seluruh semesta himpunan
- Himpunan Bagian, himpunan yang anggota sebagian dari anggota himpunan lain. Disimbolkan dengan tanda subset
- Himpunan Berhingga, himpunan yang anggotanya dapat dihitung
- Himpunan Tak Berhingga, himpunan yang anggotanya tak hingga banyak sehingga tidak dpaat dihitung
- Himpunan Kosong, himpunan yang tidak memiliki anggota, disimbolkan dengan tanda {} atau Ø
Hubungan antar Himpunan

Dua atau lebih himpunan dapat dihubungkan dengan beberapa operasi, seperti irisan, gabungan, dan selisih.
IRISAN HIMPUNAN
Irisan adalah dua himpunan yang bagian-bagiannya menjadi anggota dari keduanya. Irisan himpunan disimbolkan dengan 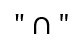
Misalkan S adalah himpunan semesta, irisan himpunan A dan B adalah himpunan yang anggotanya semua anggota S yang merupakan anggota himpunan A dan anggota himpunan B, dilambangkan dengan Irisan dua himpunan dinotasikan
GABUNGAN HIMPUNAN
Gabungan dalam teori himpunan merupakan operasi penggabungan dua himpunan, sehingga menghasilkan himpunan baru yang berisi anggota-anggota kedua himpunan awal. Gabungan dinotasikan dengan tanda union 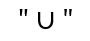
Misalkan S adalah himpunan semesta, gabungan himpunan A dan B adalah himpunan yang anggotanya semua anggota S yang merupakan anggota himpunan A atau anggota himpunan B, dilambangkan denganGabungan dua himpunan ditulis
SELISIH HIMPUNAN
Selisih (difference) himpunan A dan B adalah himpunan yang anggotanya semua anggota dari A tetapi bukan anggota dari B. Selisih himpunan dilambangkan dengan tanda kurang (-).
KOMPLEMEN HIMPUNAN
Komplemen himpunan berarti himpunan anggota selain anggota himpunan tersebut. Operasi komplemen ini mirip dengan selisih, hanya saja yang dicari adalah selisih dari semesta dari himpunan tertentu. Komplemen memerlukan ditetapkannya himpunan semesta. Komplemen himpunan A dapat disimbolkan dengan AC
Sifat Operasi Bilangan Bulat

PENJUMLAHAN dan PENGURANGAN
Penjumlahan bilangan bulat disimbolkan dengan tanda tambah (+). Sedangkan Pengurangan bilangan bulat disimbolkan dengan tanda kurang (-). Sifat-sifat dari penjumlahan dan pengurangan bilangan bulat diantaranya:
- Komutatif, a ± b = b ± a
- Asosiatif, (a ± b) ± c = a ± (b ± c)
Terdapat sifat khusus untuk penjumlahan bilangan bulat
- Dua bilangan ganjil jika dijumlahkan sama dengan bilangan genap
- Dua bilangan genap jika dijumlahkan sama dengan bilangan genap
- Penjumlahan bilangan ganjil dan genap akan menjadi bilangan ganjil
PERKALIAN
Secara umum, untuk a elemen bilangan bulat positif dan b elemen bilangan bulat, a x b diartikan menjumlahkan b sebanyak a kali.
Pada operasi perkalian juga berlaku sifat komutatif, asosiatif, dan distributif. Untuk sebarang bilangan bulat a, b, dan, c berlaku:
1. Komutatif
a x b = b x a
2. Asosiatif
(a x b) x c = a x ( b x c)
3. Distributif
Perkalian terhadap penjumlahan
a x (b + c) = a x b + a x c
Perkalian terhadap pengurangan
a x (b - c) = a x b - a x c
Perkalian dua bilangan bulat tak nol
Keterangan:
Positif (+) : Sebarang bilangan bulat positif
Negatif (-) : Sebarang bilangan bulat negatif
Sifat khusus perkalian bilangan bulat:
- bilangan ganjil dikalikan bilangan ganjil akan menghasilkan bilangan ganjil
- bilangan genap dikalikan bilangan genap akan menghasilkan bilangan genap
- bilangan ganjil dikalikan bilangan genap akan menghasilkan bilangan genap
Faktor Bilangan Bulat
Diketahui a dan b adalah bilangan bulat. a disebut faktor dari b jika ada n sedemikian sehingga b = a × n, dengan n adalah bilangan bulat.
PEMBAGIAN
Secara umum, untuk a elemen bilangan bulat positif dan b, c elemen bilangan bulat, a : b diartikan b mengurangi a sebanyak c kali sampai nol.
a : b = c
a - b - b - b (sebanyak c) = 0
dengan syarat b tidak boleh sama dengan 0
Sifat Pembagian Bilangan positif dan negatif sama dengan perkalian.
PRIORITAS DALAM OPERASI BILANGAN BULAT
Jika tidak dibuat aturan dalam urutan operasi matematika, maka dalam perhitungan matematika akan menghasilkan beberapa kemungkinan jawaban yang berbeda. Oleh karena itu, para matematikawan sepakat untuk membuat aturan tentang urutan operasi.
- Bilangan yang berada di dalam tanda kurung
- Bilangan berpangkat
- Perkalian dan Pembagian dari kiri ke kanan
- Penjumlahan dan Pengurangan dari kiri ke kanan
1.
Kerjakan soal berikut ini dengan benar!
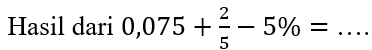
A.

B.

C.

D.

E.

JAWABAN BENAR
E.

PEMBAHASAN

2.
Kerjakan soal berikut ini dengan tepat!
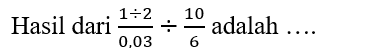
A. 1/100
B. 1/10
C. 1
D. 10
E. 100
JAWABAN BENAR
D.
10
PEMBAHASAN
3.
Kerjakan soal berikut ini dengan tepat!
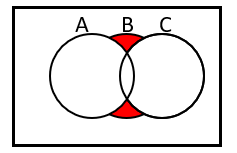
Operasi himpunan yang menyatakan daerah berwarna merah yaitu ….
A.

B.

C.

D.

E.

JAWABAN BENAR
B.

PEMBAHASAN
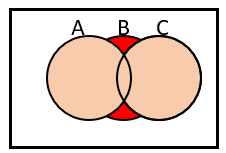
A∩C berwarna merah muda
Daerah berwarna merah diperoleh dari himpunan B dikurangi dengan daerah berwarna pink, sehingga operasi himpunannya yaitu B-(A∪C)
4.
Kerjakan soal berikut ini dengan tepat!
Diantara contoh berikut ini yang termasuk dalam himpunan adalah ….
A. Kumpulan perempuan cantik di kelas 10-A
B. Kumpulan pemain basket yang tinggi
C. Kumpulan pelari yang memiliki pace kurang dari 7
D. Kumpulan pelukis yang kreatif
E. Kumpulan siswa yang pintar di kelas 12-B
JAWABAN BENAR
C.
Kumpulan pelari yang memiliki pace kurang dari 7
PEMBAHASAN
Himpunan merupakan kumpulan dari objek tertentu yang dianggap sebagai satu kesatuan denfan keterangan yang jelas. Kata-kata sifat, seperti cantik, pintar, tinggi, kreatif, tidak dapat dikategorikan sebagai suatu himpunan karena bersifat subjektif. Sehingga contoh yang tepat adalah kumpulan pelari yang memiliki pace kurang dari 7 karena memiliki keterangan yang jelas
5.
Kerjakan soal berikut ini dengan tepat!
![]()
A. 25/18
B. 18/25
C. 12/5
D. 5/12
E. 25/22
JAWABAN BENAR
A.
25/18
PEMBAHASAN
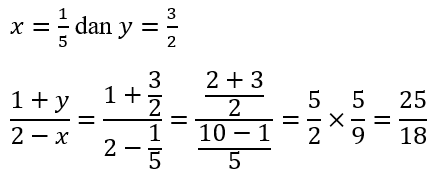

Oops!!!
Yah, jawaban kamu meleset nih. Ingin melihat pembahasan soal ini?

BENAR!!!
Selamat!
Jawaban kamu benar. Ingin lihat pembahasan soal ini?
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved

