Belajar Pintar Materi SMP, SMA, SMK
BelajarPintarV3
UTBK - SNBT
Pengetahuan Kuantitatif
MATERI
Konsep Matriks

Matriks adalah susunan bilangan-bilangan berbentuk persegi panjang yang diatur dalam baris (jajaran) dan kolom (lajur) dengan dibatasi oleh kurung biasa “( )” atau kurung siku “[ ]”.
Bilangan-bilangan yang tersusun dalam matriks disebut elemen (unsur) matriks. Baris sebuah matriks adalah susunan bilangan-bilangan yang mendatar (horizontal), sedangkan kolom adalah susunan bilangan-bilangan yang tegak (vertikal).
Jika suatu matriks diberi nama matriks A, maka secara umum, bentuk matriks A, yaitu:
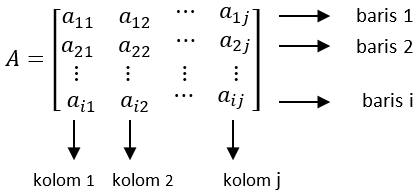
Amxn artinya matriks A mempunyai baris sebanyak m dan mempunyai kolom sebanyak n.
a11 = elemen baris pertama kolom pertama
a12 = elemen baris pertama kolom kedua
a1n = elemen baris pertama kolom ke-n
a21 = elemen baris kedua kolom pertama
...
amn = elemen baris ke-m kolom ke-n
ORDO MATRIKS
Ordo matriks adalah banyaknya elemen baris dan banyaknya elemen kolom dari suatu matriks. Jika sebuah matriks memiliki m baris dan n kolom, maka matriks tersebut berordo m x n, dapat dituliskan Amxn.
Contoh :

JENIS-JENIS MATRIKS
Matriks dapat dikelompokkan menjadi beberapa jenis sebagai berikut:
- Matriks nol, yaitu: matriks yang seluruh elemennya bilangan nol.
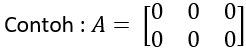
- Matriks baris, yaitu: matriks yang hanya memiliki satu baris atau berordo 1 x n.
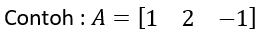
- Matriks kolom, yaitu: matriks yang hanya memiliki satu kolom atau berordo m x 1.
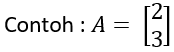
- Matriks persegi, yaitu: matriks yang banyaknya baris dan kolom sama atau berordo m x m.
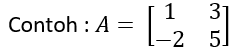
- Matriks diagonal, yaitu: matriks persegi yang semua elemennya nol, kecuali elemen pada diagonal utamanya bukan nol.
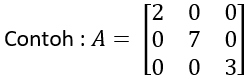
- Matriks segitiga atas, yaitu: matriks persegi yang semua elemen di bawah diagonal utamanya adalah nol.
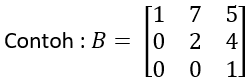
- Matriks segitiga bawah, yaitu: matriks persegi yang semua elemen di atas diagonal utamanya adalah nol.
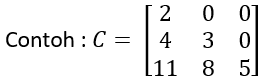
- Matriks identitas, yaitu: matriks persegi yang elemen pada diagonal utamanya adalah satu, sedangkan elemen lainnya adalah nol. Matriks identitas dilambangkan dengan “I”.
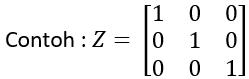
KESAMAAN DUA MATRIKS
Dua matriks dikatakan sama (A=B), apabila mempunyai ordo yang sama dan elemen-elemen yang letaknya sama (bersesuaian) besarnya sama atau aij = bij.
Contoh :
![]()
Matriks A=B karena ordo dan elemen yang letaknya bersesuaian besarnya sama. Matriks C=D karena ordo dan elemen yang seletak dari kedua matriks sama.
Matriks A≠C karena meskipun memiliki ordo yang sama, tetapi letak elemen yang sama tidak sesuai.
Operasi pada Matriks

Operasi aljabar pada matriks hanya sebatas penjumlahan, pengurangan, perkalian dan ada juga operasi aljabar khusus yang hanya di terapkan pada matriks, yaitu transpose matriks.
PENJUMLAHAN MATRIKS
Jika terdapat dua matriks, misal matriks A dan B, yang memiliki ordo sama, maka elemen-elemen yang seletak dapat dijumlahkan. Jumlah A dan B dapat dinyatakan dengan A+B.
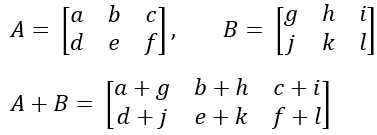
Jika A, B, C merupakan matriks dengan ordo yang sama, maka berlaku sifat penjumlahan, yaitu:
- Komutatif : A+B = B+A
- Asosiatif : (A+B)+C = A+(B+C)
- Identitas : A+O = O+A = A, dengan O adalah matriks nol
- (A+B)t = At + Bt
PENGURANGAN MATRIKS
Jika terdapat dua matriks, misal matriks A dan B, yang memiliki ordo sama, maka elemen-elemen yang seletak dapat dikurangkan.
Pengurangan A dan B dapat dinyatakan dengan A – B atau A + (– B).
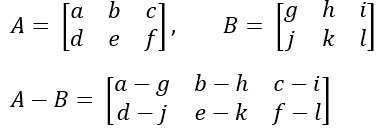
Jika A, B, C merupakan matriks dengan ordo yang sama, maka berlaku sifat pengurangan, yaitu:
- A – A = O, dengan O adalah matriks nol
- Identitas : A – O = A
- (A – B)t = At – Bt
PERKALIAN SKALAR PADA MATRIKS
Jika diketahui A merupakan suatu matriks dan K merupakan bilangan real, maka hasil perkalian K dengan matriks A adalah matriks yang diperoleh dengan mengalikan setiap elemen A dengan K.
Apabila A dan B merupakan matriks dengan ordo yang sama dan k, m merupakan bilangan real, maka berlaku:
- (k+m)A = k.A + m.A
- k(A+B) = k.A + k.B
- (-1)A = A (-1) = -A, dengan –A adalah negatif dari matriks A
- k(m.A) = (k.m)A
- (kA)t = k . At
PERKALIAN ANTAR MATRIKS
Dua buah matriks, misal matriks A dan B, dapat dikalikan jika banyaknya kolom matriks A sama dengan banyaknya baris matriks B.
Bentuk perkalian antar matriks secara umum yaitu:
Ai×m × Bm×n = Ci×n
Untuk mencari hasil kali matriks A dengan matriks B ialah mengalikan elemen pada baris-baris matriks A dengan elemen pada kolom-kolom matriks B kemudian jumlahkan hasil perkalian antara baris dan kolom tersebut.
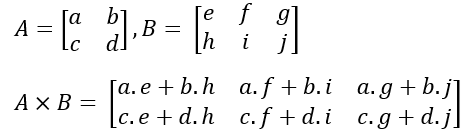
PERPANGKATAN MATRIKS
Pemangkatan matriks hanya berlaku pada matriks persegi. Jika A merupakan matriks persegi dan n, x, y adalah bilangan bulat maka berlaku:
Ax.Ay = A(x+y)
(Ax)y = Ax.y
An = A.An-1 , dengan n>0
A0 = 1
TRANSPOSE MATRIKS
Transpose suatu matriks, misal matriks A, yang dilambangkan dengan At adalah sebuah matriks yang disusun dengan cara menukarkan baris matriks A menjadi kolom matriks At dan kolom matriks A menjadi baris matriks At.
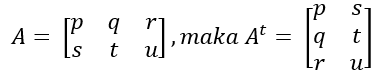
Determinan Matriks

DETERMINAN MATRIKS ORDO 2X2
Determinan suatu matriks didefinisikan sebagai selisih antara perkalian elemen-elemen pada diagonal utama dengan perkalian elemen-elemen pada diagonal sekunder. Determinan matriks hanya dapat ditentukan pada matriks persegi.
Determinan dari matriks A dapat dituliskan det(A) atau |A|.
Determinan matriks persegi dengan ordo 2x2 dapat dihitung dengan cara berikut:
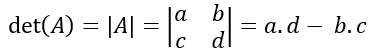
Berikut ini sifat-sifat dari determinan matriks

DETERMINAN MATRIKS ORDO 3X3
Diketahui matriks A dengan ordo 3x3 sebagai berikut:

Determinan matriks persegi dengan ordo 3x3 dapat dicari dengan menggunakan 2 cara, yaitu:
Kaidah Sarrus
Langkah-langkah mencari determinan matriks ordo 3x3 dengan kaidah Sarrus:
- Meletakkan kolom pertama dan kolom kedua di sebelah kanan garis vertikal determinan
- Jumlahkan hasil kali elemen-elemen yang terletak pada diagonal utama dengan hasil kali elemen-elemen yang sejajar diagonal utama pada arah kanan kemudian kurangi dengan jumlah hasil kali elemen-elemen yang terletak pada diagonal samping dengan elemen-elemen yang sejajar dengan diagonal samping
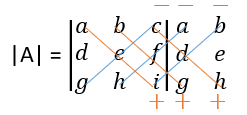
|A| = (a.e.i) + (b.f.g) +( c.d.h) – (c.e.g) – (a.f.h) – (b.d.i)
|A| = (a.e.i + b.f.g + c.d.h) – (c.e.g + a.f.h + b.d.i)
Ekspansi Minor Kofaktor
Apabila diketahui sebuah matriks persegi A maka minor elemen aij dinyatakan oleh Mij dan didefinisikan sebagai determinan submatriks yang tinggal setelah baris ke-i dan kolom ke-j dihilangkan dari matriks A
Minor a23 = M23 dapat dicari dengan menghilangkan baris kedua dan kolom ketiga sehingga diperoleh M23. Kemudian dicari nilai determinannya
Sedangkan kofaktor dari sebuah elemen adalah nilai minor beserta tandanya. Tanda dari determinan ditentukan dengan memberikan tanda positif (+) pada elemen baris pertama kolom pertama diikuti perubahan tanda ke bawah (vertikal) dan ke kanan (horizontal).
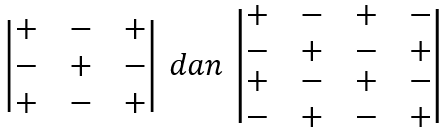
Untuk menentukan determinan matriksnya, kita harus memilih satu baris atau kolom. Misalkan dipilih baris pertama, maka:
![]()
Invers Matriks
Invers matriks dilambangkan dengan A-1. Suatu matriks dikatakan memiliki invers jika determinan dari matriks tersebut tidak sama dengan nol.
INVERS MATRIKS ORDO 2x2
Invers matriks persegi dengan ordo 2x2 dapat dicari dengan cara sebagai berikut:
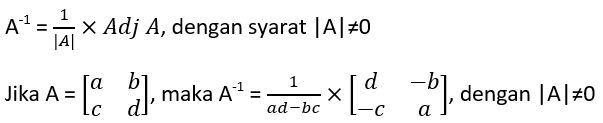
INVERS MATRIKS ORDO 3x3
Untuk mencari invers matriks pada ordo 3x3 menggunakan metode eliminasi Gauss Jordan atau ekspansi kofaktor.
Metode Gauss-Jordan
Secara sistematis, eliminasi Gauss Jordan dapat dinyatakan sebagai berikut:
[A | I] → [I | A-1]
Jadi matriks persegi A dieliminasi menggunakan operasi aljabar sampai membentuk matriks identitas. Operasi yang dilakukan pada matriks A juga dilakukan pada matriks identitas sehingga jika matriks A sudah menjadi matriks identitas, matriks identitas akan berubah menjadi invers dari matriks A.
Operasi yang dapat digunakan pada eliminasi Gauss-Jordan yaitu:
- Bertukar baris
- Menjumlahkan suatu baris dengan baris lain yang telah dikalikan dengan bilangan skalar
Metode Ekspansi Kofaktor
Pada metode ekspansi kofaktor, cara yang digunakan hampir sama dengan menentukan determinan matriks menggunakan ekspansi kofaktor. Namun, dalam menentukan invers matriks, menggunakan rumus berikut
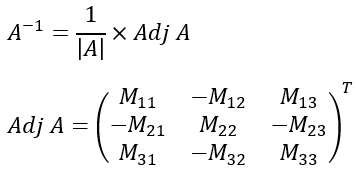
Persamaan dan Penggunaan Matriks

Sistem Persamaan Linear Dua Variabel (SPLDV) maupun Sistem Persamaan Linear Tiga Variabel (SPLTV) dapat kita selesaikan menggunakan persamaan matriks dengan metode Cramer. Metode Cramer memanfaatkan konsep determinan pada matriks untuk menyelesaikan masalah SPLDV maupun SPLTV. Sebelum menggunakan matriks, kita harus bisa mengubah persamaan linear menjadi persamaan matriks.

Hampir sama dengan masalah SPLDV di atas, masalah SPLTV juga dapat diselesaikan dengan mengubah menjadi persamaan matriks terlebih dahulu.

Selain dengan metode Cramer, masalah SPLDV juga dapat diselesaikan dengan menggunakan Invers Matriks.
Dengan prinsip perkalian dua matriks,
![]()
Untuk menentukan x dan y menggunakan invers matriks dapat dicari dengan rumus:
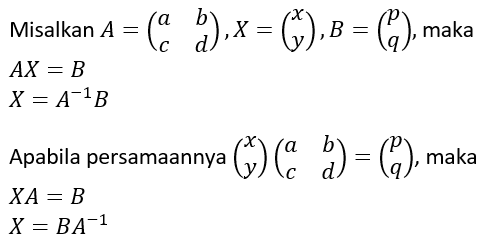
1.
Kerjakan soal berikut!
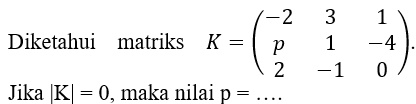
A. -30
B. -20
C. -18
D. 18
E. 30
JAWABAN BENAR
C.
-18
PEMBAHASAN
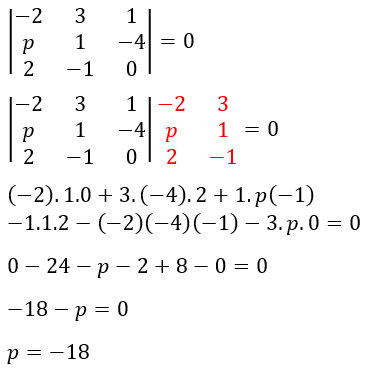
2.
Kerjakan soal berikut!
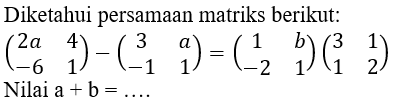
A. 0
B. 3
C. 4
D. 5
E. 6
JAWABAN BENAR
B.
3
PEMBAHASAN

3.
Kerjakan soal berikut!
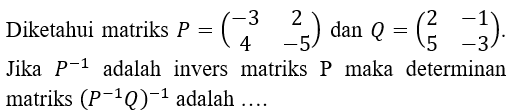
A. -6
B. -7
C. -8
D. -9
E. -10
JAWABAN BENAR
B.
-7
PEMBAHASAN
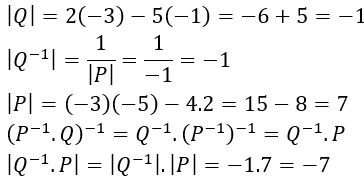
4.
Kerjakan soal berikut!
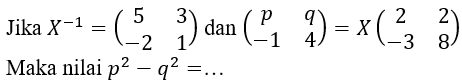
A. -3
B. -2
C. 1
D. 2
E. 3
JAWABAN BENAR
A.
-3
PEMBAHASAN
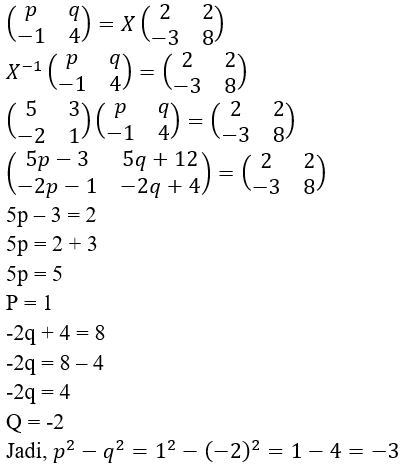
5.
Kerjakan soal berikut!
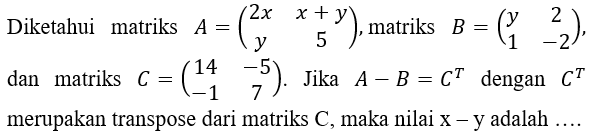
A. -9
B. -7
C. 5
D. 7
E. 9
JAWABAN BENAR
E.
9
PEMBAHASAN
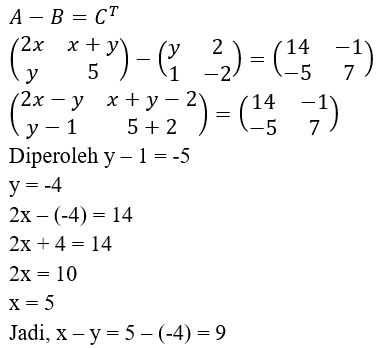

Oops!!!
Yah, jawaban kamu meleset nih. Ingin melihat pembahasan soal ini?

BENAR!!!
Selamat!
Jawaban kamu benar. Ingin lihat pembahasan soal ini?
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved

