Belajar Pintar Materi SMP, SMA, SMK
BelajarPintarV3
UTBK - SNBT
Pengetahuan Kuantitatif
MATERI
Permutasi

Permutasi adalah susunan berurutan dari semua atau sebagian elemen dari suatu himpunan.
Untuk menyelesaikan soal permutasi terdapat 4 metode, yaitu:
Permutasi dari Elemen yang Berbeda
Permutasi elemen dari elemen yang ada (setiap elemen berbeda) adalah susunan elemen itu dalam suatu urutan yang diperhatikan. Banyaknya permutasi dari elemen n diambil r elemen dapat dinotasikan:
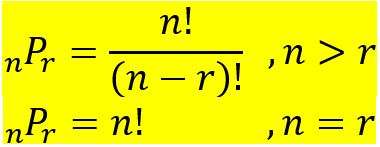
Permutasi dengan Berapa Elemen yang Sama
Setiap unsur yang digunakan tidak boleh lebih dari satu kali. Secara umum, banyaknya permutasi n elemen yang memuat k, l, m, … elemen yang sama dapat dinotasikan:
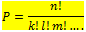
Permutasi Siklis
Permutasi siklis digunakan untuk menghitung banyak cara yang dibuat dari susunan melingkar. Secara umum, banyaknya permutasi siklis dapat dinotasikan:
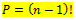
Permutasi Berulang
Permutasi berulang adalah permutasi yang dalam penyusunannya urutan diperhatikan dan suatu objek dapat dipilih lebih dari sekali (berulang). Banyaknya permutasi ini dinotasikan:
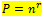
Sedangkan permutasi yang tidak boleh berulang dapat dinotasikan:
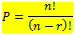
Kombinasi

Kombinasi adalah banyaknya cara yang berbeda dalam memilih kelompok dengan mengambil beberapa atau semua anggota himpunan tanpa memperhatikan urutan.
Kombinasi dapat dirumuskan sebagai berikut:
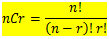
Sebagai ilustrasi : kombinasi 2 elemen dari 3 huruf a,b,c adalah ab, ac, bc . Sedangkan ba, ca, cb tidak termasuk hitungan karena pada kombinasi ab=ba, ac = ca, bc = cb. Banyak kombinasi adalah :
3C2 = 3! / 2! (3-2)! = 3!/2! = 3 x 2 x 1 / 2 x 1 = 3
Peluang

Peluang adalah nilai (kuantitas) untuk menyatakan seberapa besar terjadinya suatu peristiwa. Peluang juga biasa disebut sebagai probabilitas.
Misalkan A suatu kejadian yang merupakan himpunan bagian dari ruang sampel S. Artinya setiap anggota A juga merupakan anggota dari S (A subset S).
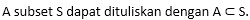
Maka peluang dapat dirumuskan sebagai berikut:

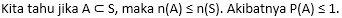
Terdapat beberapa kejadian khusus, yaitu:

Berdasarkan penjelasan diatas, maka besar nilai peluang suatu kejadian A adalah

FREKUENSI HARAPAN
Frekuensi harapan dari kejadian A merupakan banyaknya kejadian A yang diharapkan terjadi dalam beberapa kali percobaan.
Frekuensi harapan kejadian A didefinisikan sebagai berikut:
F(A) = n x P(A)
Keterangan:
F(A) = frekuensi harapan kejadian A
n = banyaknya percobaan yang dilakukan
P(A) = peluang kejadian A
PELUANG KOMPLEMEN SUATU KEJADIAN
Komplemen dari suatu kejadian A memiliki arti bahwa kejadian A tidak terjadi. Komplemen kejadian A dapat dinyatakan dengan Ac.
Peluang kejadian bukan A (Komplemen A) dapat dirumuskan sebagai berikut.
P(Ac)=1 - P(A)
Keterangan:
P(Ac) = komplemen A
P(A) = peluang kejadian A
PELUANG KEJADIAN MAJEMUK
Peluang Kejadian Majemuk berarti menghitung probabilitas dari dua kejadian dengan syarat-syarat tertentu. Peluang kejadian majemuk terbagi menjadi :
- Peluang Dua Kejadian Tidak Saling Lepas
- Peluang Dua Kejadian Saling Lepas
- Peluang Dua Kejadian Saling Bebas
- Peluang Dua Kejadian Bersyarat
Peluang Dua Kejadian Tidak Saling Lepas
Dua kejadian yang memiliki semesta yang sama serta dua kejadian tersebut saling beririsan disebut kejadian tidak saling lepas.
Perhatikan diagram venn berikut!
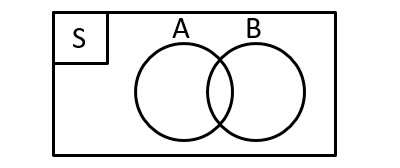
Misalkan kejadian A dan kejadian B berada pada ruang sampel S. Kejadian A dan B dikatakan tidak saling lepas jika terdapat minimal satu elemen pada kejadian A yang sama dengan elemen yang ada pada kejadian B. Kejadian A harus beririsan dengan Kejadian B.
Peluang kejadian A atau B yang mungkin terjadi dengan A dan B adalah kejadian tidak saling lepas, dapat dirumuskan sebagai berikut:

Misalnya akan diambil satu kartu bridge secara acak. Kejadian A adalah kejadian terambilnya kartu yang bergambar hati dan kejadian B terambilnya kartu J,Q,K. Terdapat kemungkinan terambil kartu Queen yang bergambar hati. Oleh karena itu, kejadian A dan B dapat dikatakan sebagai kejadian tidak saling lepas.
Peluang Dua Kejadian Saling Lepas
Dua kejadian dikatakan saling lepas apabila kejadian A dan kejadian B tidak beririsan meskipun himpunan semestanya sama.
Perhatikan diagram venn berikut!
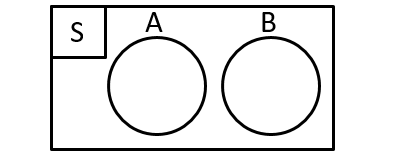
Misalkan kejadian A dan kejadian B berada pada ruang sampel S. Kejadian A dan B dikatakan saling lepas jika tidak ada elemen pada kejadian A yang sama dengan elemen yang ada pada kejadian B. Secara ringkas, Kejadian A dan kejadian B tidak saling beririsan.
Peluang kejadian A atau B yang mungkin terjadi dengan A dan B adalah kejadian saling lepas, dapat dirumuskan sebagai berikut:

Misalnya pada sebuah kotak terdapat bola warna merah dan biru. Kejadian A adalah kejadian terambilnya bola merah dan kejadian B terambilnya bola biru. Jika akan diambil 1 bola secara acak, maka akan terambil 1 bola berwarna merah saja atau 1 bola berwarna biru saja. Kejadian A dan B dapat dikatakan sebagai kejadian saling lepas.
Peluang Dua Kejadian Saling Bebas
Dua kejadian dikatakan saling bebas apabila kejadian A memiliki semesta yang berbeda dengan kejadian B.
Peluang kejadian A atau B yang mungkin terjadi dengan A dan B adalah kejadian saling bebas, dapat dirumuskan sebagai berikut:
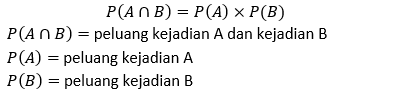
Misalkan pada pelemparan dua buah dadu, kejadian munculnya mata dadu genap pada dadu pertama tidak akan mempengaruhi kejadian munculnya mata dadu ganjil pada dadu kedua karena dadu pertama dan dadu kedua memiliki semesta yang berbeda
Peluang Dua Kejadian Bersyarat
Dua kejadian dikatakan tidak saling bebas atau bersyarat apabila munculnya kejadian A mempengaruhi terjadinya kejadian B atau sebaliknya. Kejadian B dapat terjadi setelah kejadian A terjadi atau sebaliknya.
Misalkan pada sebuah kantong terdapat bola dengan warna merah, kuning, dan hijau. Akan diambil 2 bola secara bergantian tanpa dikembalikan. Maka kejadian terambilnya bola kedua akan bergantung dari kejadian terambilnya bola pertama.
Jika kejadian A dan B adalah dua kejadian yang saling bersyarat, dapat dirumuskan sebagai berikut:

1.
Kerjakan soal berikut ini!
Susunan huruf-huruf A, G, S, O, dan P dengan huruf A dan S selalu berdampingan. Banyaknya susunan huruf yang dapat dibentuk adalah ….
A. 6
B. 12
C. 24
D. 48
E. 96
JAWABAN BENAR
D.
48
PEMBAHASAN

2.
Kerjakan soal berikut ini!
Diberikan angka 2 – 8. Banyaknya bilangan ribuan genap lebih dari 500 yang dapat disusun dengan angka yang berlainan adalah ….
A. 320
B. 280
C. 240
D. 160
E. 140
JAWABAN BENAR
B.
280
PEMBAHASAN

3.
Kerjakan soal berikut ini!
Pada sebuah meja berbentuk bundar akan diisi 8 orang laki-laki dan perempuan. Apabila 4 orang dari mereka adalah dua pasang suami istri yang duduknya harus bersebelahan. Maka banyaknya urutan tempat duduk yang dapat terjadi adalah ….
A. 5040
B. 480
C. 240
D. 120
E. 60
JAWABAN BENAR
B.
480
PEMBAHASAN
Apabila ada 2 pasang suami istri yang duduknya harus berdampingan, maka terdapat 4 orang akan terhitung 2 paket orang
Sehingga banyak permutasi siklisnya yaitu
(6-1)!=5!=120
Karena posisi duduk suami istri dapat bertukar, maka banyak posisi duduk yang mungkin terjadi yaitu
120×2×2=480 cara
4.
Kerjakan soal berikut ini!
Sandi akan mengadakan reuni dengan teman-temannya sebanyak 8 orang. Mereka saling berjabat tangan satu sama lain. Kejadian jabat tangan yang terjadi dilakukan sebanyak ….
A. 32
B. 30
C. 28
D. 26
E. 24
JAWABAN BENAR
C.
28
PEMBAHASAN
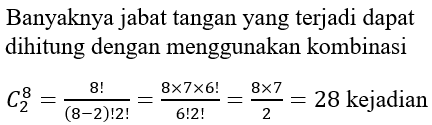
5.
Kerjakan soal berikut ini!
Banyak kata yang dapat disusun dari huruf LABALABA adalah ….
A. 20160
B. 6720
C. 1680
D. 840
E. 420
JAWABAN BENAR
E.
420
PEMBAHASAN


Oops!!!
Yah, jawaban kamu meleset nih. Ingin melihat pembahasan soal ini?

BENAR!!!
Selamat!
Jawaban kamu benar. Ingin lihat pembahasan soal ini?
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved

