APSiswaNavbarV2

redesain-navbar Portlet

BelajarPintarV3

UTBK - SNBT

Pengetahuan Kuantitatif

Daftar Materi

MATERI

Persamaan Lingkaran

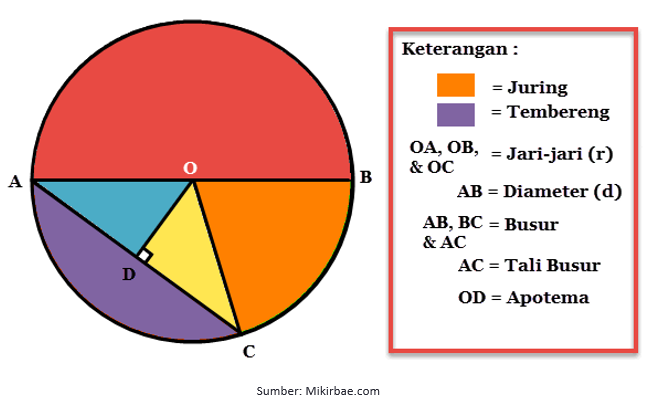
Sobat Pintar masih ingat atau tidak, apa sih pengertian dari lingkaran itu?

Lingkaran adalah tempat kedudukan titik-titik yang berjarak sama dengan satu titik tertentu. Yang dimaksud titik tertentu adalah titik pusat, sedangkan jarak yang sama adalah jari-jari lingkaran.

Sama halnya dengan gelombang sinus yang memiliki persamaan, lingkaran juga memiliki persamaan.

Bagaimana persamaannya?

Persamaan lingkaran dapat ditentukan jika diketahui titik pusat dan jari-jari lingkarannya.

LINGKARAN DENGAN PUSAT DI TITIK O(0,0)

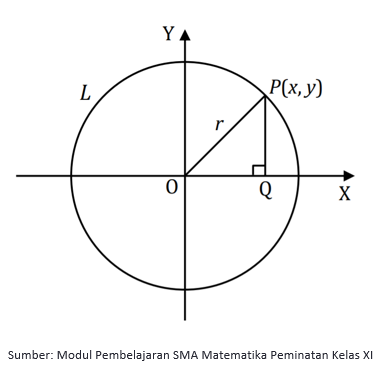
Perhatikan gambar di atas!

Lingkaran L berpusat di O(0, 0) dan berjari-jari r.

Misal titik P(x, y) adalah sebarang titik yang terletak pada lingkaran L, panjang ruas garis OP akan sama dengan jari-jari
Dapat dibentuk segitiga POQ siku-siku di Q, berdasarkan teorema pythagoras diperoleh:

OQ2 + PQ2 = OP2 

Dari sini didapatkan persamaan lingkaran yang berpusat di titik O(0,0) dan berjari-jari r:

 

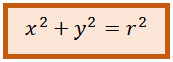
LINGKARAN DENGAN PUSAT DI TITIK M(a,b)

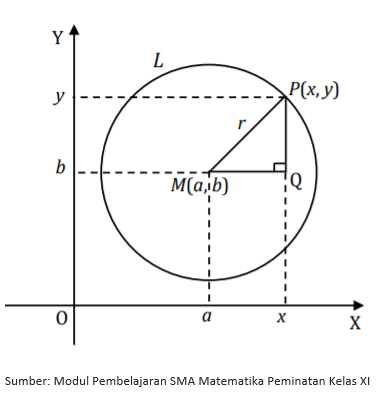
Perhatikan gambar di atas!

Lingkaran L berpusat di titik M(a, b) dengan jari-jari r.

Misal titik P(x, y) adalah sembarang titik yang terletak pada lingkaran L, maka

MP = r 
MQ = x – a 
PQ = y – b 

Dengan informasi di atas dan segitiga PMQ, kita bisa menggunakan teorema pythagoras dan mendapatkan persamaan lingkaran yang berpusat di titik M(a, b) dan berjari-jari r

MQ2 + PQ2 = MP2 

 

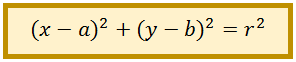
BENTUK UMUM PERSAMAAN LINGKARAN

Bentuk umum persamaan lingkaran yang berpusat di titik M(a,b) dengan jari-jari r dapat dicari dengan cara berikut:

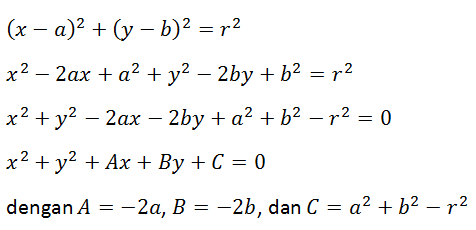
Jadi, bentuk umum dari persamaan lingkaran, yaitu:

 

RUMUS PENTING

Jarak dua titik

Misalkan diketahui titik A(xa,ya) dan titik B(xb, yb), maka jarak titik AB, yaitu:

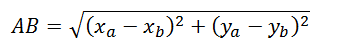
Jarak titik dengan garis

Misalkan diketahui titik C(xc, yc) dan garis Ax + By + C = 0, maka jarak titik C ke garis tersebut, yaitu:

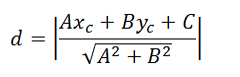
Garis Singgung Persekutuan Dua Lingkaran

GARIS SINGGUNG PERSEKUTUAN LUAR LINGKARAN

Perhatikan gambar di bawah ini!

Lingkaran A berpusat di A dengan jari-jari AD = r1. Lingkaran B berpusat di B dengan jari-jari BE = r2.

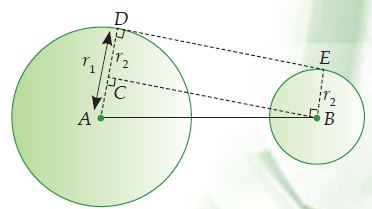
AB adalah jarak kedua titik pusat lingkaran (s). DE adalah garis singgung persekutuan luar dua lingkaran, dimana DE tegak lurus dengan AD. Melalui titik B, dapat ditarik garis BC yang sejajar garis DE (BC//DE), sehingga BE = CD = r2, dan sudut ACB = 90o.

Maka segitiga ACB adalah segitiga siku-siku, sehingga berlaku teorema Phythagoras,
AB2 = AC2 + BC2
BC2 = AB2 – AC2
        = AB2 – (AD – CD)2
        = s2 – (r1 – r2)2

Karena BC//DE dan sudut ACB = sudut ADE = 90o, maka DE = BC. Jadi, DE2 = s2 – (r1 – r2)2. Maka panjang garis singgung persekutuan luar dua lingkaran dirumuskan:

l2 = s2 – (r1 – r2)2

dengan r1 > r2, dan
l : panjang garis singgung persekutuan luar dua lingkaran
s : jarak antara kedua pusat dua lingkaran
r1: jari-jari lingkaran pertama
r2: jari-jari lingkaran kedua

 

GARIS SINGGUNG PERSEKUTUAN DALAM LINGKARAN

Perhatikan gambar di bawah ini!

Lingkaran A berpusat di A dengan jari-jari AC = r1. Lingkaran B berpusat di B dengan jari-jari BE = r2

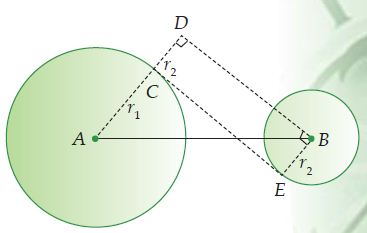
AB adalah jarak kedua titik pusat lingkaran (s). CE adalah garis singgung persekutuan dalam dua lingkaran, dimana CE tegak lurus dengan AC. Melalui titik B, kita dapat menarik garis BD yang sejajar dengan garis CE. (BD//CE), sehingga CD = BE = r2, dan sudut ADB = 90o.

Maka segitiga ADB adalah segitiga siku-siku, sehingga berlaku teorema Phythagoras, yaitu:
AB2 = AD2 + BD2
BD2 = AB2 – AD2
        = AB2 – (AC + CD)2
        = s2 – (r1 + r2)2

Karena BD//CE dan sudut ADB = sudut ACE = 90o, maka CE = BD. Jadi, CE2 = s2 – (r1 + r2)2. Sehingga, dapat kita simpulkan bahwa panjang garis singgung persekutuan dalam dua lingkaran adalah:

d2 = s2 – (r1 + r2)2

dengan r1 > r2, dan
d : panjang garis singgung persekutuan dalam dua lingkaran
s : jarak antara kedua pusat dua lingkaran
r1 : jari-jari lingkaran pertama
r2 : jari-jari lingkaran kedua

Hubungan Dua Lingkaran

Seperti pada garis, dua lingkaran juga dapat saling berhubungan loh sobat. Apalagi kalau dua lingkaran saling berkaitan, jadi nampak seperti cincin pernikahan hihi..

Langsung aja kita bahas hubungan antara dua lingkaran ya, Sobat!

Misalkan terdapat dua lingkaran, lingkaran L1 berpusat di A dengan jari-jari R dan lingkaran L2 berpusat di B dengan jari-jari r. Kedudukan dua lingkaran dapat ditentukan oleh nilai deskriminan, yaitu D = b2 – 4ac. Persamaan dari salah satu lingkaran dapat disubstitusikan pada persamaan lingkaran yang lain, kemudian hasilnya dapat menentukan kedudukan dari kedua lingkatan dengan ketentuan:

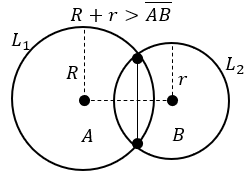
  1. Jika D > 0, kedua lingkaran saling berpotongan di dua titik. Sehingga diperoleh: 
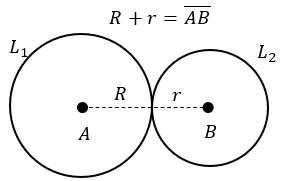
  2. Jika D = 0, kedua lingkaran bersinggungan di satu titik. Sehingga terdapat dua kemungkinan, yaitu : 
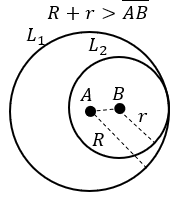
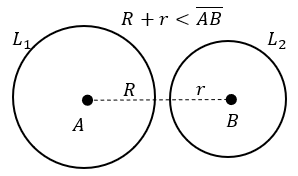
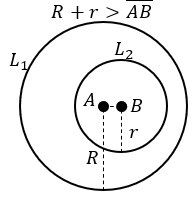
  3. Jika D < 0, kedua lingkaran saling lepas, sehingga terdapat dua kemungkinan berikut: 

Kedudukan Titik dan Garis pada Lingkaran

KEDUDUKAN TITIK PADA LINGKARAN

Kita dapat mengetahui kedudukan titik terhadap suatu lingkaran lho, Sobat!

Kita dapat mengetahui kedudukan suatu titik terhadap lingkaran dengan mempertimbangkan jarak antara titik dan titik pusat lingkaran dengan jari-jari lingkaran tersebut.

Misalkan diketahui titik A(x1,y1) dan lingkaran dengan pusat P(a,b) yang berjari-jari r, maka:

1. Titik di luar lingkaran, jika dan hanya jika panjang AP lebih besar dari jari-jari lingkaran, secara sistematis dapat dituliskan:

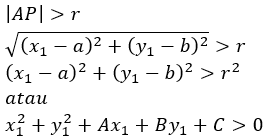
2. Titik terletak pada lingkaran, jika dan hanya jika panjang AP sama dengan jari-jari lingkaran, secara sistematis dapat dituliskan:

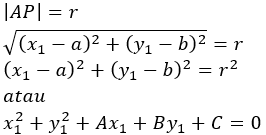
3. Titik di dalam lingkaran, jika dan hanya jika panjang AP kurang dari jari-jari lingkaran, secara sistematis dapat dituliskan:

 

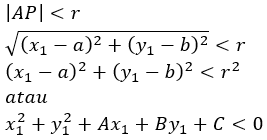
KEDUDUKAN GARIS PADA LINGKARAN

Selain titik, kita juga dapat mengetahui kedudukan suatu garis terhadap lingkaran, Sobat!

Kedudukan dari garis terhadap lingkaran terbagi menjadi 3 macam, yaitu : garis di luar lingkaran, garis yang menyinggung lingkaran dan garis yang memotong lingkaran.

Untuk mengetahui kedudukan sebuah garis terhadap lingkaran, kita harus mensubstitusikan terlebih dahulu persamaan garis y = mx + c pada persamaan lingkaran sehingga diperoleh persamaan dengan bentuk ax2 + bx + c = 0.

Nah, kedudukan garis terhadap lingkaran ditentukan dari nilai deskrimininan persamaan kuadrat ax2 + bx + c = 0.

Kalau Sobat Pintar lupa, nih kakak ingatkan kembali rumus dari determinan persamaan kuadrat:

D = b2 – 4ac

-    Jika D > 0, maka garis memotong lingkaran di dua titik

-    Jika D = 0, maka garis menyinggung lingkaran atau memotong lingkaran di satu titik

-    Jika D < 0, maka garis berada di luar lingkaran.

Persamaan Garis Singgung Lingkaran

Sebelumnya, Sobat Pintar sudah mencari tahu kedudukan garis terhadap lingkaran, salah satunya adalah garis yang menyinggung lingkaran. Jika dalam mencari kedudukan garis terhadap lingkaran akan diketahui persamaan garisnya, pada materi kali ini kita akan mencari persamaan dari garis yang menyinggung lingkaran.

Garis singgung sendiri adalah garis yang memotong lingkaran hanya di satu titik. Dalam mencari persamaan garis singgung lingkaran, kita dapat menentukannya dengan cara-cara berikut:

PERSAMAAN GARIS SINGGUNG JIKA DIKETAHUI TITIK PADA LINGKARAN

Titik pada lingkaran dapat juga disebut dengan titik potong antara garis dengan lingkaran. Untuk menentukan persamaan garis singgung jika diketahui titik P(x1,y1) pada lingkaran dapat dicari bergantung persamaan lingkarannya, yaitu:

 

 PERSAMAAN GARIS SINGGUNG JIKA DIKETAHUI GRADIENNYA

Persamaan  garis singgung lingkaran jika diketahui  gradiennya dapat ditentukan dengan rumus berikut:

 

PERSAMAAN GARIS SINGGUNG JIKA DIKETAHUI TITIK DI LUAR LINGKARAN

Terdapat 3 cara untuk menentukan persamaan garis singgung jika diketahui titik di luar lingkaran, tiga cara tersebut antara lain:

  1. Menggunakan diskriminan
  • Lakukan pemisalan persamaan garis dengan gradien m dan melalui titik A(x1, y1)
    y – y1 = m (x – x1) 
    y = mx – mx1 + y1
  • Substitusi persamaan garis tersebut ke persamaan lingkaran sehingga diperoleh persamaan kuadrat dengan variabel x
  • Karena garis menyinggung lingkaran, artinya diskriminan dari persamaan kuadrat tadi harus bernilai nol atau D = 0
  • Cari nilai m, dan kembalikan nilai m ke persamaan garis singgung pada langkah awal
  1. Menggunakan rumus persamaan garis singgung dengan gradien diketahui
  • Lakukan pemisalan persamaan garis dengan gradien m dan melalui titik A(x1, y1)
    y – y1 = m (x – x1) 
    y = mx – mx1 + y1
  • Lakukan pemisalan persamaan garis singgung lingkaran dengan gradien m
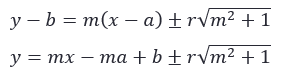
  • Samakan kedua garis singgung untuk mendapat nilai m
  • Kembalikan nilai m ke pemisalan awal
  1. Menggunakan bantuan persamaan garis kutub
  • Cari persamaan garis kutub titik A(x1, y1) dengan rumus
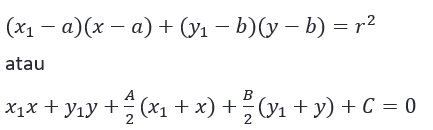
  • Substitusi persamaan garis ke kutub ke persamaan lingkaran untuk mendapatkan titik potong garis kutub dan lingkaran
  • Dari titik potong yang sudah didapatkan sobat pintar bisa menggunakan rumus garis singgung dengan titik pada lingkaran

Ketiga cara ini akan lebih mudah dipahami jika sobat pintar perhatikan contoh soal berikut:

Tentukan persamaan garis singgung pada lingkaran x2 + y2 = 25 yang melalui titik (–1, 7) di luar lingkaran!

Cara 1:

Cara 2:

Cara 3:

1.

Kerjakan soal berikut ini!

Diketahui sebuah lingkaran berjari-jari 4. Jika lingkaran tersebut berpusat di titik (2,-1), maka bentuk umum persamaan lingkaran tersebut adalah ....


A. x2 + y2 – 4x + 2y – 11 = 0
B. x2 + y2 + 4x + 2y + 11 = 0
C. x2 + y2 – 4x - 2y – 11 = 0
D. x2 + y2 + 4x - 2y – 11 = 0
E. x2 + y2 + 4x - 2y + 11 = 0

JAWABAN BENAR

A.

x2 + y2 – 4x + 2y – 11 = 0

PEMBAHASAN

Pusat (2,-1), r = 4

(x – a)2 + (y – b)2 = r2

(x – 2)2 + (y – (-1))2 = 42

(x – 2)2 + (y + 1)2 = 16

x2 – 4x + 4 + y2 + 2y + 1 – 16 = 0

x2 + y2 – 4x + 2y – 11 = 0

2.

Kerjakan soal berikut ini!

Kedudukan garis y = -x + 3 pada lingkaran x2 + y2 = 9 adalah ....


A. di luar lingkaran
B. menyinggung lingkaran
C. memotong lingkaran di dua titik
D. sejajar dengan lingkaran
E. tegak lurus dengan lingkaran

JAWABAN BENAR

C.

memotong lingkaran di dua titik

PEMBAHASAN

Substitusikan persamaan garis y = -x + 3 pada persamaan lingkaran x2 + y2 = 9

x2 + (-x+3)2 = 9

x2 + x2 - 6x + 9 – 9 = 0

2x2 - 6x = 0

D = b2 – 4 ac

D = (-6)2 – 4.2.0

D = 36 > 0

Jadi, garis y = -x + 3 memotong lingkaran x2 + y2 = 9

3.

Kerjakan soal berikut ini!

Sebuah lingkaran memiliki persamaan x2 + y2 – 6x + 10y – 2 = 0, pusat dan jari-jari lingkaran tersebut berturut-turut adalah ....


A. (5,-3) dan 6
B. (3,-5) dan 6
C. (-6,10) dan 36
D. (10,-6) dan 36
E. (-3,5) dan 6

JAWABAN BENAR

B.

(3,-5) dan 6

PEMBAHASAN

4.

Kerjakan soal berikut ini!

Diketahui lingkaran L memiliki persamaan x2 + y2 – 2x + 6y – 6 = 0. Persamaan garis singgung lingkaran L yang bergradien 1/2, yaitu ....


A.
B.
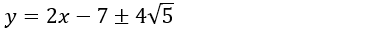
C.
D.
E.

JAWABAN BENAR

D.

PEMBAHASAN

5.

Kerjakan soal berikut ini!

Lingkaran M berpusat di (3,0) dengan jari-jari 5 dan lingkaran N berpusat di (4,-3) dengan jari-jari 3. Hubungan antara kedua lingkaran adalah ....


A. berpotongan di dua titik
B. berpotongan di satu titik
C. saling lepas
D. lingkaran M di dalam lingkaran N
E. lingkaran N di dalam lingkaran M

JAWABAN BENAR

A.

berpotongan di dua titik

PEMBAHASAN

redesain-navbar Portlet