APSiswaNavbarV2

redesain-navbar Portlet

BelajarPintarV3

Matematika IPA

Program Linear

Daftar Materi

MATERI

Nilai Optimum Fungsi Objektif

Fungsi objektif yaitu fungsi linear dan batasan-batasan pertidaksamaan linear yang memiliki sebuah himpunan penyelesaian. Himpunan penyelesaian yang ada ialah berupa titik-titik dalam diagram cartesius yang apabila koordinatnya disubstitusikan kedalam fungsi linear maka dapat memenuhi persyaratan yang ditentukan.

Nilai optimum fungsi objektif dari suatu persoalan linear bisa ditentukan dengan menggunakan metode grafik. Dengan melihat grafik dari fungsi objektif dan batasan-batasannya, maka kita bisa tentukan letak titik yang menjadi nilai optimum.

Langkah-langkahnya yaitu sebagai berikut :

  • Menggambar himpunan penyelesaian dari semua batasan syarat yang ada pada cartesius.
  • Menentukan titik-titik ekstrim yang merupakan perpotongan pada garis batasan dengan garis batasan yang lainnya. Titik-titik ekstrim tersebut adalah himpunan penyelesaian dari batasannya dan memiliki suatu kemungkinaan besar akan membuat fungsi menjadi optimum.
  • Meneliti nilai optimum fungsi objektif dengan dua acara, yaitu :
  1. Menggunakan garis selidik, dan
  2. Membandingkan nilai fungsi objektif pada tiap titik ekstrim.

mari kita bahasa satu persatu sobat pintar

1. Menggunakan garis selidik

Garis selidik dapat diperoleh dari fungsi objektif f(x, y) = ax + by yang mana garis selidiknya ialah: ax + by = Z

Nilai Z diberikan sembarang nilai.

Garis ini dibuat setelah grafik himpunan penyelesaian pertidaksamaannya juga dibuat.

Garis selidik awal dibuat di area himpunan penyelesaian awal. Lalu kemudian dibuat garis-garis yang sejajar dengan garis selidik awal.

Berikut adalah pedoman untuk mempermudah penyelidikian nilai fungsi optimum:

1. Cara 1 (syarat a > 0), yaitu:

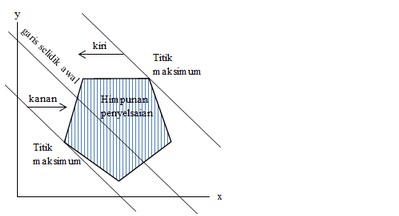
  • Apabila maksimum, maka dibuat garis yang sejajar garis selidik awal sehingga membuat himpunan penyelesaian berada di kiri garis tersebut. Titik yang dilalui garis tersebut ialah titik maksimum.
  • Apabila minimum, maka dibuatlah garis yang sejajar garis selidik awal sehingga akan membuat suatu himpunan penyelesaian berada di kanan garis tersebut.
  • Titik yang dilalui garis tersebut ialah titik minimum.

Perhatikan grafik dibawah:

2. Cara ke- 2 (syarat b > 0), yaitu:

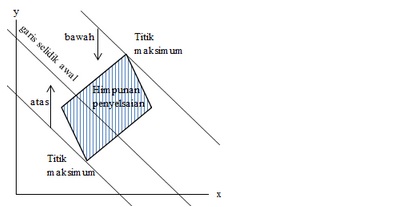
  • Apabila maksimum: maka dibuat garis yang sejajar garis selidik awal sehingga membuat himpunan penyelesaian berada di bawah garis tersebut. Titik yang dilalui garis tersebut ialah titik maksimum.
  • Apabila minimum: maka dibuat garis yang sejajar garis selidik awal sehingga membuat himpunan penyelesaian berada di atas garis tersebut. Titik yang dilalui garis tersebut ialah titik minimum.

Perhatikanlah grafik dibawah berikut:

Bagi nilai a < 0 dan b < 0 maka berlaku sebuah kebalikan dari kedua cara yang dijelaskan di atas.

2. Membandingkan nilai fungsi tiap titik ekstrim

Menyelidiki nilai optimum dari fungsi objektif juga dapat dilaksanakan dengan terlebih dahulu menentukan titik-titik potong dari suatu garis-garis batas yang ada. Titik-titik potong tersebut merupakan nilai ekstrim yang berpotensi memiliki nilai maksimum pada salah satu titiknya.

Berdasarkan titik-titik tersebut, maka dapat ditentukan nilai masing-masing fungsinya, yakni kemudian dibandingkan.

Nilai terbesar merupakan nilai maksimum dan nilai terkecil adalah merupakan nilai minimum.

1.

Tentukanlah sebuah nilai minimum dari: f(x, y) = 9x + y pada daerah yang telah dibatasi oleh 2 < x < 6, dan 0 < y < 8 serta x + y < 7.


A. 17
B. 18
C. 19
D. 20
E. 25

JAWABAN BENAR

B.

18

PEMBAHASAN

  • Langkah pertama gambar grafiknya terlebih dahulu :

 

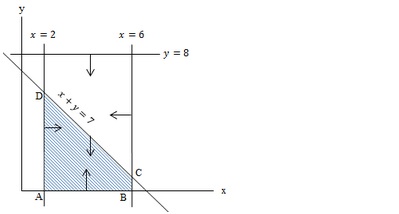
  • Langkah ke dua menentukan titik-titik ekstrimnya:

Maka berdasarkan gambar di atas, ada 4 titik ekstrim, yaitu A, B, C, D dan himpunan penyelesaiannya ada di area yang telah diarsir

  • Langkah ke tiga yaitu menyelidiki nilai optimum:

berdasarkan grafik di atas dapat diketahui titik A dan B mempunyai nilai y = 0 sehingga kemungkinan menjadi nilai minimum.

Kedua titik disubtitusikan ke dalam f(x,y) = 9x + y untuk dibandingkan

titik A(x,y) = A(2,0) disubtitusikan f(2,0) = 9(2) + 0 = 18

titik B(x,y) = B(6,0) disubtitusikan f(6,0) = 9(6) + 0 = 54

dengan membandingkan tersebut, maka disimpulkan bahwa titik A memiliki nilai minimun 18.

Jawaban : B

2.

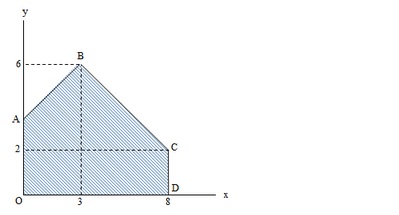
Tentukanlah dimana nilai maksimum fungsi f(x, y) = 4x + 5y yang akan dicapai pada pada grafik ini!

 


A. 38
B. 40
C.

41


D. 42
E. 46

JAWABAN BENAR

D.

42

PEMBAHASAN

Titik ekstrim pada gambar adalah :

  • A tidak mungkin maksimum karena titik A paling kiri
  • B(3,6)
  • C(8,2)
  • D(8,0)

Nilai tiap titik ekstrim adalah :

B(3,6) maka f(3,6) = 4(3) + 5(6) = 42

C(8,2) maka f(8,2) = 4(8) + 5(2) = 42

D(8,0) maka f(8,0) = 4(8) + 5(0) = 32

sehingga dapat diketahui hasilnya bahwa nilai maksimumnya berada pada titik yang melalui garis BC dengan nilai maksimum 42

Jawaban : D

redesain-navbar Portlet