Belajar Pintar Materi SMP, SMA, SMK
BelajarPintarV3
Matematika
Integral
MATERI
Integral Tak Tentu
Halo sobat pintar, apakah sobat pintar masih ingat dengan konsep integral yang diterapkan dalam mata pelajaran fisika kelas 11? apasih integral itu? integral merupakan anti turunan. Jadi, apabila terdapat fungsi F(x) yang dapat didiferensialkan pada interval [a, b] , sedemikian hingga
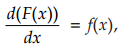
maka antiturunan dari f(x) adalah F(x) + c. Secara matematis dituliskan sebagai berkut
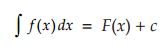
yang dimana 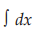 = Lambang integral yang menyatakan operasi antiturunan
= Lambang integral yang menyatakan operasi antiturunan
f(x) = Fungsi integran, yaitu fungsi yang dicari antiturunannya
c = Konstanta
apakah sobat pintar masih bingung? jika iya coba perhatikan contoh berikut
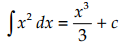
hal tersebut disebabkan karena
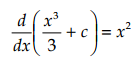
Sehingga sobat pintar dapat menyebut integral tak tentu sebagai wakil keseluruhan keluarga fungsi (satu antiturunan untuk setiap nilai konstanta c). Pengertian tersebut dapat sobat pintar gunakan untuk membuktikan beberapa teori yang akan membantu dalam pengerjaan hitung integral.
Integral Tentu
Apakah sobat pintar pernah menghitung suatu luasan di bawah garis yang lurus? tentu saja mudah bukan, dengan menggunakan rumus gabungan atau menggunakan rumus bangn datar biasa. Namun bagaimana jika luasan di bawah garis yang sobat pintar hitung adalah luasan yang berada di bawah garis melengkung? untuk dapat menghitung luasan yang ada di bawah grafik sobat pintar perlu mempelajari integral tentu. Apasih integral tentu itu? Integral tentu adalah integral yang dibatasi dengan batas atas dan batas bawah.
Misalkan y = F(x) anti turunan dari y = f(x) dan masing-masing terdefinisi pada daerah : 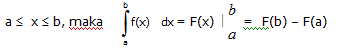
Bentuk integral di atas disebut integral tertentu dari y = f(x)
a dan b disebut batas integral dengan a merupakan batas bawah dan b merupakan batas atas.
Bagaimana nih sobat pintar, sudah faham belum dengan materi yang telah di sampaikan ? biar lebih gampangnya, yuk lihat contoh soal berikut!
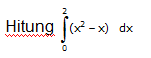
jawab : 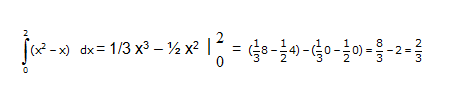
jika sobata pintar masih bingung, yuk lihat contoh soal kedua!
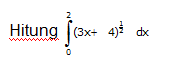
jawab : 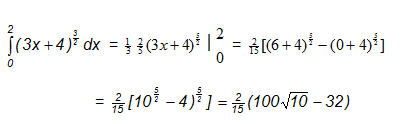
bagaimana sobat pintar? mudah bukan?
Menentukan Luas Daerah dengan Integral Tentu
masih berhubungan dengan sub bab integral tentu, integral tentu diaplikasikan untuk menghitung luas dan volume dibawah sumbu untuk lebih jelasnya, coba sobat pintar perhatikan contoh berikut

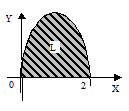
jawab : 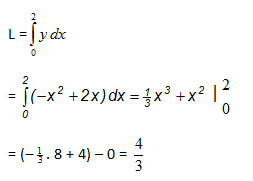
apakah sobat pintar sudah paham? jika belum, coba lihat contoh selanjutnya
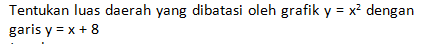
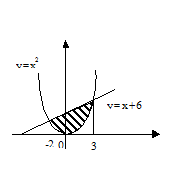
jawab :
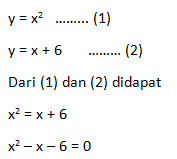
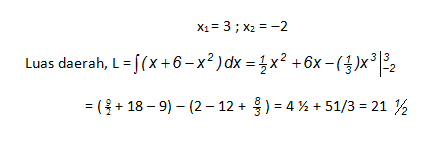
Menentukan Volume Benda Putar

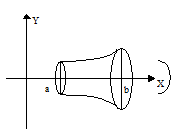
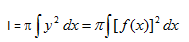
Bagaimana nih sobat pintar, sudah faham belum dengan materi yang telah di sampaikan ? yuk kita perhatikan contoh soal berikut
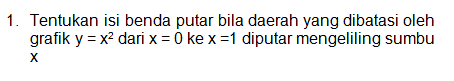
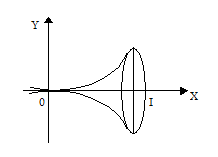
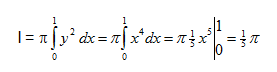
bagaimana? mudah kan sobat pintar?
Sifat Integral
1. 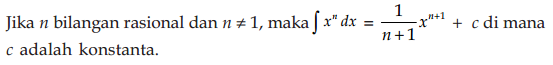
2. 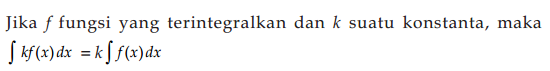
3. 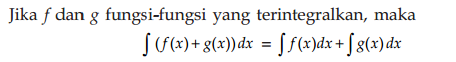
4. 
1. Volume benda putar bila luasan yang dibatasi oleh  adalah
adalah
A. 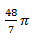
B. 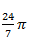
C. 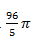
D. 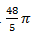
E. 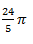
JAWABAN BENAR
D.
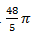
PEMBAHASAN

2. Nilai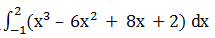 adalah
adalah
A. 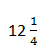
B. 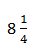
C. 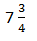
D. 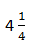
E. 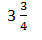
JAWABAN BENAR
E.
PEMBAHASAN
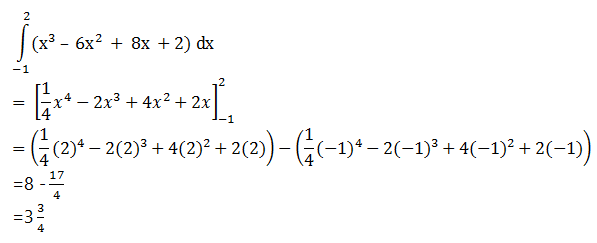

Oops!!!
Yah, jawaban kamu meleset nih. Ingin melihat pembahasan soal ini?

BENAR!!!
Selamat!
Jawaban kamu benar. Ingin lihat pembahasan soal ini?
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved

