Daftar Materi
MATERI
Menyelesaikan Persamaan Menggunakan Penjumlahan atau Pengurangan
Hallo Sobat Pintar! Kalian masih bingung gak sih gimana cara menyelesaikan Persamaan Linier satu Variabel? Berikut penjelasannya agar kalian gak bingung lagi yuk kita simak.
Dalam menyelesaikan persamaan linear satu variabel, tujuannya adalah menyederhanakan persamaan untuk menyisakan variabel saja di salah satu sisi. Setiap langkah yang digunakan untuk menyederhanakan persamaan menghasilkan persamaan ekuivalen. Apakah yang dimaksud dengan persamaan ekuivalen?
Perhatikan persamaan-persamaan berikut.
1. x + 1 = 3
2. x + 2 = 4
3. 2x - 2 = 6
Bagaimanakah himpunan selesaian dari ketiga persamaan di atas? Ketiga persamaan tersebut memiliki himpunan selesaian yang sama. Persamaan-persamaan di atas disebut dengan persamaan yang ekuivalen atau persamaan yang setara.
Untuk memahami bagaimana persamaan yang ekuivalen digunakan untuk menentukan himpunan selesaian suatu persamaan mari kita simak contoh soal dibawah ini
Contoh Soal :
1. Tentukan Penyelesaian dari persamaan berikut.
a. x - 4 = 7
b. 8 = x - 7
2. Tentukan himpunan selesaian dari 12 + x = 40
3. Andi memakan 8 kue baruasa dan Nyoman memakan 11 kue baruasa dari kemasan yang baru dibuka. Mereka berdua menyisakan 23 kue baruasa di dalam kemasan. Tulis persamaan dan tentukan selesaiannya untuk mengetahui banyaknya kue baruasa dalam kemasan semula.
Penyelesaian :
1. a. x - 4 = 7
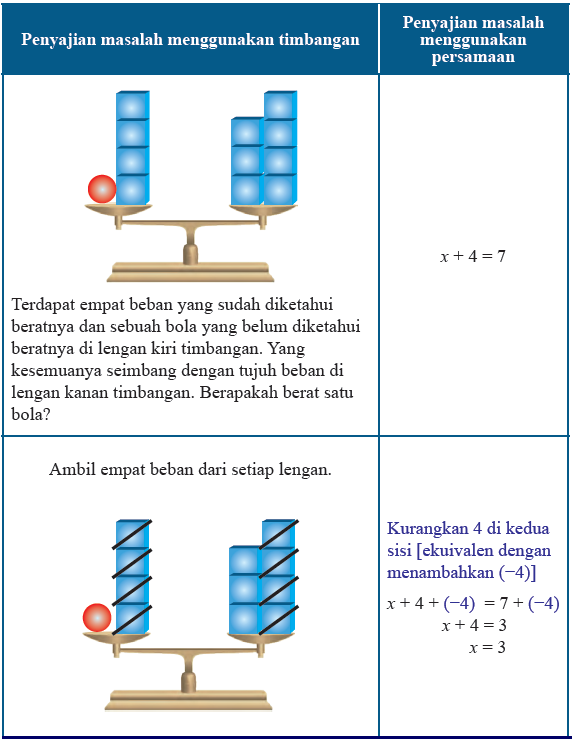
b. 8 = x - 7
2. 12 + x = 40
12 - 12 + x = 40 - 12
x = 28
Periksa
12 + x = 40
12 + (28) = 40
40 = 40 (benar)
Jadi, himpunan Penyelesaiannya adalah {28}.
3. Kata-kata Banyak kue semula dikurangi banyak kue yang dimakan Andi dikurangi banyak kue yang dimakan Nyoman sama dengan
banyak kue yang tersisa.
Variabel Misalkan b adalah banyak kue dalam kemasan semula
Persamaan b - 8 - 11 = 23
b - 8 - 11 = 23
b - 19 = 23
b - 19 + 19 = 23 + 19
b = 42
Jadi, banyak kue dalam kemasan semula adalah 42 kue.
Menyelesaikan Persamaan Menggunakan Perkalian atau Pembagian
Pada kegiatan sebelumnya kalian telah menerapkan operasi penjumlahan dan pengurangan pada persamaan yang ekuivalen untuk menyelesaikan suatu persamaan. Pada kegiatan ini akan diperluas lagi dengan menggunakan operasi perkalian dan pembagian untuk menyelesaikan persamaan.
Agar lebih memahami mari Sobat Pintar pelajari contoh soal dibawah ini
Contoh Soal :
Tentukan selesaian dari persamaan 2(x - 4) + 5x = 34
Penyelesaian :
Sebelum menyelesaikannya, kita harus menyederhanakan bentuk aljabar di sisi kiri.
2(x - 4) + 5x = 34
2x - 8 + 5x = 34
7x - 8 = 34
7x - 8 + 8 = 34 + 8
7x = 42
7/42 = 7/7
x = 42/7
x = 6
Jadi, himpunan selesaian dari persamaan adalah {6}.
Contoh Soal :
Tentukan ukuran setiap sudut pada segitiga di samping. Gunakan busur derajat untuk memeriksa kebenaran jawaban.
Penyelesaian :
Jumlah ketiga sudut segitiga adalah 180o. Sehingga persamaan yang dapat terbentuk adalah sebagai berikut.
m + 2 m + (m + 10) = 180
m + 2 m + m + 10 = 180
4 m + 10 = 180
4m = 180 - 10
4m = 170
m = 170/4
m = 42,5
Jadi, besar ketiga sudut segitiga antara lain 42 1/2o , 85o, dan 52 1/2o .
1.
Kerjakanlah Soal berikut ini dengan benar!
Tentukan himpunan penyelesaian dari 2x - 1 = 5
A. x = { }
B. x = {3}
C. x = {5}
D. x = {2}
JAWABAN BENAR
B.
x = {3}
PEMBAHASAN
2x - 1 = 5
2x = 5 + 1
2x = 6
x = 3
Sehingga himpunan x = {3}
2.
Kerjakanlah Soal berikut ini dengan benar!
Tentukan nilai 5x – 2 jika x merupakan penyelesaian dari 3x + 6 = 12 !
A. 0
B. 2
C. 4
D. 8
JAWABAN BENAR
D.
8
PEMBAHASAN
Menentukan nilai x terlebih dahulu.
3x + 6 = 12
3x + 6 – 6 = 12 – 6
3x = 6
x = 6 : 3
x = 2
Subtitusi x = 2 pada 5x – 2
5(2) – 2 = 10 – 2 = 8
3.
Kerjakanlah Soal berikut ini dengan benar!
Himpunan penyelesaian dari 6x+14 = 68 adalah…..
A. x = {8 }
B. x = {5}
C. x = {9}
D. x = {7}
JAWABAN BENAR
C.
x = {9}
PEMBAHASAN
6x+14 = 68
6x = 68-14
6x = 54
x = 54/6
x = 9
4.
Kerjakanlah Soal berikut ini dengan benar!
Tentukan nilai 7x+4 jika x merupakan penyelesaian dari 4x-5=23 !
A. x = {58 }
B. x = {52}
C. x = {53}
D. x = {49}
JAWABAN BENAR
C.
x = {53}
PEMBAHASAN
Menentukan nilai x terlebih dahulu.
4x – 5 = 23
4x – 5 + 5 = 23 + 5
4x = 28
x = 28/4
x = 7
Subtitusi x = 7 pada 7x+4
7(7) + 4 = 49 + 4 = 53
5.
Kerjakanlah Soal berikut ini dengan benar!
Tentukan nilai x dari
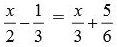
A. 4
B. 7
C. 9
D. 14
JAWABAN BENAR
B.
7
PEMBAHASAN
Untuk menyelesaikan persamaan, kalian bisa mengalikan setiap sisi dengan 6, yakni KPK dari 2, 3, dan 6.
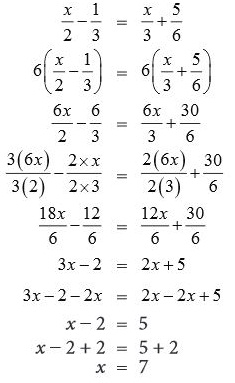
Jadi, himpunan selesaiannya adalah {7}.
Untuk lebih meyakinkan, ganti variabel x pada persamaan semula dengan 7.
6.
Kerjakanlah Soal berikut ini dengan benar!
Tentukan nilai x dari persamaan 2(5x – 6) = 3(4x – 5) – 3 !
A. 2
B. 3
C. 5
D. 7
JAWABAN BENAR
B.
3
PEMBAHASAN
2(5x – 6) = 3(4x – 5) – 3
2(5x) + 2(-6) = 3(4x) + 3(-5) – 3
10x – 12 = 12x – 15 – 3
10x – 12 = 12x – 18
10x – 12 + 12 = 12x – 18 + 12
10x = 12x – 6
10x -12x = 12x – 6 – 12x
-2x = -6
x = -6 : (-2)
x = 3
7.
Kerjakanlah Soal berikut ini dengan benar!
Tentukan Penyelesaian dari persamaan 5(x + 2) + 12x = 61 !
A. 14
B. 17
C. 19
D. 18
JAWABAN BENAR
B.
17
PEMBAHASAN
Sebelum menyelesaikannya, kita harus menyederhanakan bentuk aljabar di sisi kiri.
5(x + 2) + 12x = 61
5x + 10 + 12x = 61
17x + 10 = 61
17x + 10 - 10 = 61 - 10
17x = 51
17/17 x = 51/17
x = 51/7
x = 3
Jadi, himpunan Penyelesaian dari persamaan adalah {17}.
8.
Kerjakanlah Soal berikut ini dengan benar!
Tentukan Penyelesaian dari persamaan 2(5 - x) = 4(2x - 5)!
A. 4
B. 7
C. 3
D. 8
JAWABAN BENAR
C.
3
PEMBAHASAN
2(5 - x) = 4(2x - 5)
10 – 2x = 8x – 20
10 + 20= 8x + 2x
30 = 10x
30/10 = 10/10 x
3 = x
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
Ikuti Kami
Download Aku Pintar
