Belajar Pintar Materi SMP, SMA, SMK
BelajarPintarV3
Matematika
Persamaan dan Pertidaksamaan Linear Satu Variabel
MATERI
Menyelesaikan Masalah Pertidaksamaan Linear Satu Variabel

Perbedaan penting antara persamaan linear satu variabel dengan pertidaksamaan linear satu variabel ditunjukkan ketika kita mengali atau membagi kedua sisi pertidaksamaan dengan bilangan bukan nol.
a. Ketika kalian mengalikan atau membagi kedua sisi dengan bilangan positif, maka tanda ketidaksamaan tidak berubah. Perhatikan tabel berikut.

Sifat ini juga berlaku untuk < dan >
b. Ketika kalian mengalikan atau membagi kedua sisi dengan bilangan negatif, maka tanda ketidaksamaan berubah. Perhatikan tabel berikut..

Sifat ini juga berlaku untuk < dan >
Untuk lebih memahami tentang masalah pertidaksamaan linear satu variabel mari kita simak contoh soal dibawah ini
Contoh Soal :
Selesaikan pertidaksamaan x - 4 < - 2. Gambar selesaiannya dalam garis bilangan dan tuliskan selesaiannya dalam notasi interval.
Penyelesaian :
x - 4 < - 2
x - 4 + 4 < - 2 + 4
x < 2
Jadi, selesaiannya adalah x < 2 atau (- , 2).
, 2).

Contoh Soal :
Tentukan himpunan selesaian dari peridaksamaan linear berikut dengan x adalah bilangan bulat.
-6(x - 3) > 2 - 2 (x - 8)
Penyelesaian :
-6(x - 3) > 2 - 2 (x - 8)
-6x + 18 > 2 - 2x + 16
-6x + 18 > 18 - 2x
-6x + 2x + 18 > 18 - 2x + 2x
-4x + 18 > 18
-4x + 18 -18 > 18 -18
-4x > 0
-4x/-4 < 0/-4
x < 0
Jadi, himpunan selesaian dari pertidaksamaan -6(x - 3) > 2 - 2 (x - 8) adalah
Contoh Soal :
Pak Ferdy memiliki sebuah mobil box pengangkut barang dengan daya angkut tidak lebih dari 800 kg. Berat Pak Fredy adalah 60 kg dan dia akan mengangkut kotak barang yang setiap kotak beratnya 20 kg. Tentukan pertidaksamaan dari situasi di atas. Tentukan banyak kotak paling banyak yang dapat diangkut oleh Pak Fredy dalam sekali pengangkutan.
Penyelesaian :
a. Misalkan: x = banyaknya kotak barang yang diangkut dalam mobil box. Sehingga, pertidaksamaan dari situasi tersebut adalah sebagai berikut.
Banyak kotak dikali berat tiap kotak ditambah berat Pak Ferdy tidak lebih dari daya angkut mobil.
x x 20 + 60 < 800
Jadi, pertidaksamaan dari situasi Pak Ferdy adalah 20 x + 60 < 800
b. Untuk menentukan banyak kotak paling banyak yang dapat diangkut oleh mobil box Pak Ferdy adalah dengan menentukan selesaian pertidaksamaan.
20 x + 60 < 800
20 x + 60 - 60 < 800 - 60
20 x < 740
x < 37
x paling besar yang memenuhi pertidaksamaan x < 37 adalah 37.
Jadi, banyak kotak yang dapat diangkut Pak Fredy dalam sekali pengangkutan paling banyak 37 kotak.
1.
Kerjakanlah Soal berikut ini dengan benar!
Selesaikan pertidaksamaan berikut ini!
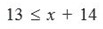
A. x > 1
B. x > -1
C. x < 1
D. x < -1
JAWABAN BENAR
B.
x > -1
PEMBAHASAN

2.
Kerjakanlah Soal berikut ini dengan benar!
Nilai x yang memenuhi pertidaksamaan 5x – 4 > 7x + 12 adalah...
A. x > -8
B. x < -8
C. x > -4
D. x < -4
JAWABAN BENAR
B.
x < -8
PEMBAHASAN
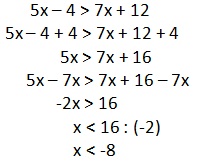
3.
Kerjakanlah Soal berikut ini dengan benar!
Nilai x yang memenuhi pertidaksamaan x – 9 > 7x + 45 adalah...
A. x > 6
B. x > -6
C. x < 6
D. x < -6
JAWABAN BENAR
D.
x < -6
PEMBAHASAN
x + 9 > 7x + 45
x-7x > 45-9
-6x > 36
x < 36/-6
x < -6
4.
Kerjakanlah Soal berikut ini dengan benar!
Nilai x yang memenuhi pertidaksamaan -2x > 7x +81 adalah...
A. x > -9
B. x < -9
C. x < 9
D. x > 9
JAWABAN BENAR
B.
x < -9
PEMBAHASAN
-2x > 7x +81
-2x-7x > 81
-9x > 81
-9/-9 x < 81/-9
x < -9

Oops!!!
Yah, jawaban kamu meleset nih. Ingin melihat pembahasan soal ini?

BENAR!!!
Selamat!
Jawaban kamu benar. Ingin lihat pembahasan soal ini?
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved

