Belajar Pintar Materi SMP, SMA, SMK
BelajarPintarV3
Matematika
Persamaan Garis Lurus
MATERI
Grafik Persamaan Garis Lurus

Apa yang Sobat Pintar tahu tentang persamaan garis lurus?
Berikut penjelasan tentang grafik persamaan garis lurus beserta sifat-sifatnya.
Salah satu manfaat koordinat Kartesius adalah untuk menggambar garis lurus. Untuk membuat garis lurus dengan persamaan tertentu, misal y = 2x dapat dinyatakan dalam persamaan linear dua variabel yaitu 2x - y = 0. Bagaimana cara menentukan dua selesaian dari persamaan linear dua variabel tersebut?
Bentuk umum persamaan y = 2x + 1 dapat dituliskan sebagai y = mx + c dengan x dan y variabel, c konstanta dan m adalah koefisien arah atau kemiringan.
Mari kita perhatikan contoh soal dibawah ini
Contoh Soal :
Lengkapi tabel berikut dan gambar grafik persamaan 4x - y = 5.

Penyelesaian :
Untuk x = -1, kita peroleh 4x - y = 5
4 (-1) - y = 5 substitusi x = -1
-4 - y = 5 sederhanakan
-4 + 4 -y = 5 + 4 tambahkan kedua ruas oleh 4
y = -9 kalikan kedua ruas oleh -1
Untuk y = 0, kita peroleh 4x - y = 5 tulis persamaan
4x - 0 = 5 substitusi y = 0
4x = 5 sederhanakan
x = 5/4 bagi kedua ruas oleh 4
Tabel setelah dilengkapi adalah
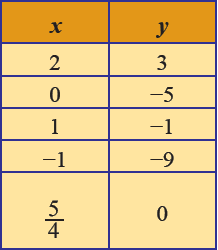
Dari tabel di atas, diperoleh pasangan berurutan (2, 3), (0, -5), (1, -1), (-1, -9), dan (5/4, 0) yang merupakan titik-titik pada koordinat Kartesius yang membentuk garis lurus. Setiap pasangan berurutan tersebut adalah selesaian persamaan 4x - y = 5.
Titik-titik selesaian tersebut jika dihubungkan akan membentuk garis lurus. Gambar garis yang melalui titik-titik adalah sebagai berikut.
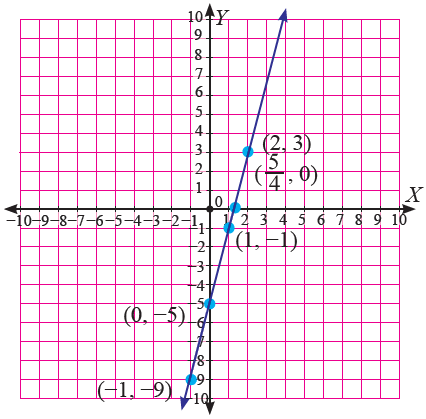
Gambar Garis lurus pada koordinat Kartesius
Garis lurus tersebut menunjukkan semua selesaian persamaan 4x - y = 5. Setiap titik pada garis merupakan selesaian persamaan.
Sifat-sifat Persamaan Garis Lurus

Untuk mengetahui sifat-sifat persamaan garis lurus perlu kalian ketahui kembali bentuk umum dari persamaan garis lurus, yaitu y = mx + c. Pada kegiatan pertama ini kalian akan mengetahui sifat-sifat persamaan garis lurus dilihat dari persamaannya dan dilihat dari perubahan nilai salah satu koefisen atau konstanta.
Tabel Sifat-sifat persamaan garis lurus
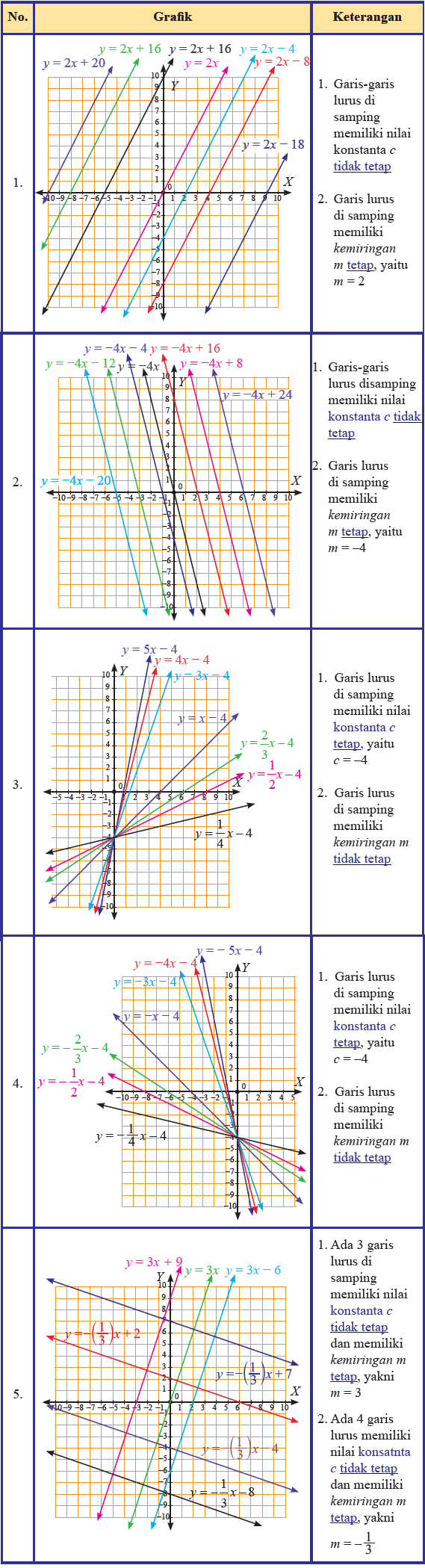
1.
Kerjakan soal dibawah ini dengan benar!
Grafik fungsi yang menyatakan f(x) = 3x - 2, x merupakan anggota bagian bilangan real (R) adalah...
A.
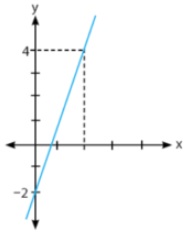
B.
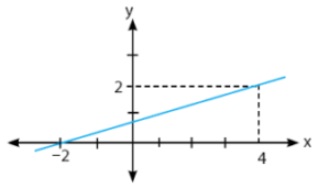
C.
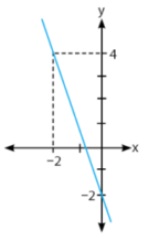
D.
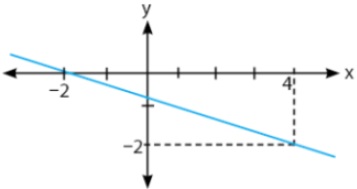
JAWABAN BENAR
A.

PEMBAHASAN
f(x) = 3x - 2
Menentukan titik
| x | 0 | 1 | 2 |
| y | -2 | 1 | 4 |
2.
Perhatikan gambar di bawah ini!
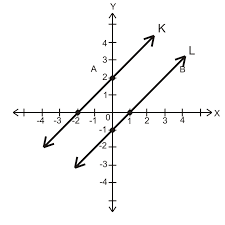
Pernyataan di bawah ini yang benar mengenai persamaan dua garis adalah ...
A. Garis-garis lurus tersebut memiliki nilai konstanta c tetap dan kemiringan m tetap
B. Garis-garis lurus tersebut memiliki nilai konstanta c berubah dan kemiringan m berubah
C. Garis-garis lurus tersebut memiliki nilai konstanta c berubah tetapi kemiringan m tetap
D. Garis-garis lurus tersebut memiliki nilai konstanta c tetap tetapi kemiringan m berubah
JAWABAN BENAR
C.
Garis-garis lurus tersebut memiliki nilai konstanta c berubah tetapi kemiringan m tetap
PEMBAHASAN
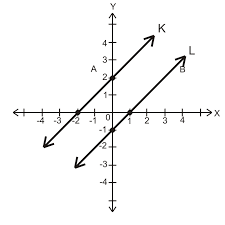
Berdasarkan gambar di atas merupakan dua garis yang sejajar sehingga garis-garis lurus tersebut memiliki nilai konstanta c berubah tetapi kemiringan m tetap.
3.
Kerjakan soal dibawah ini dengan benar!
Jika sebuah garis memiliki persamaan 2y + 4x – 20 = 0. Maka koordinat titik potong terhadap sumbu x adalah ...
A. (-1, -2)
B. (2, 0)
C. (3, 1)
D. (5, 0)
JAWABAN BENAR
D.
(5, 0)
PEMBAHASAN
Agar mendapatkan titik potong terhadap sumbu x maka syaratnya y=0, maka
2y + 4x – 20 = 0
2.0 + 4x – 20 = 0
4x – 20 = 0
4x = 20
x = 20/4
x = 5
maka koordinat titik potong terhadap sumbu x adalah ( 5, 0)
4.
Kerjakan soal dibawah ini dengan benar!
Grafik garis dengan persamaan 4x – 3y =12 adalah.....
A.

B.

C.

D.

JAWABAN BENAR
D.

PEMBAHASAN
Mencari titik potong terhadap sumbu x maka syaratnya y=0, maka
4x – 3y =12
4x – 3.0 =12
4x = 12
x = 12/4
x = 3
maka koordinat titik potong terhadap sumbu x adalah ( 3, 0)
Mencari titik potong terhadap sumbu y maka syaratnya x=0, maka
4x – 3y =12
4 . 0 – 3y =12
-3y = 12
y = 12/-3
x = -4
maka koordinat titik potong terhadap sumbu x adalah ( 0, -4)
dari pilihan diatas gambar yang memiliki titik potong (3, 0 ) dan (0, -4) adalah Opsi D

Oops!!!
Yah, jawaban kamu meleset nih. Ingin melihat pembahasan soal ini?

BENAR!!!
Selamat!
Jawaban kamu benar. Ingin lihat pembahasan soal ini?
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved

