Belajar Pintar Materi SMP, SMA, SMK
BelajarPintarV3
Matematika
Persamaan Garis Lurus
MATERI
Kemiringan Persamaan Garis Lurus

Tangga untuk tempat tidur tingkat seperti tampak pada gambar di samping merupakan salah satu contoh penerapan garis lurus dalam kehidupan sehari-hari. Agar tangga aman, nyaman, dan tidak berbahaya jika dinaiki, maka harus ditentukan dengan tepat kemiringan tangga tersebut.
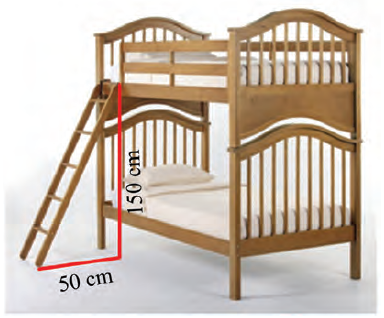
Gambar Tempat tidur dengan tangga
Persamaan berikut menyatakan pengertian gradien (kemiringan garis).
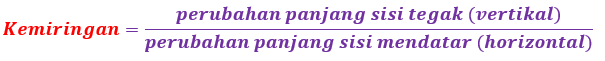
Untuk memahami lebih jelas tentang kemiringan suatu garis coba amati beberapa garis lurus berikut.
Tabel Kemiringan persamaan garis lurus yang melalui titik (0, 0)
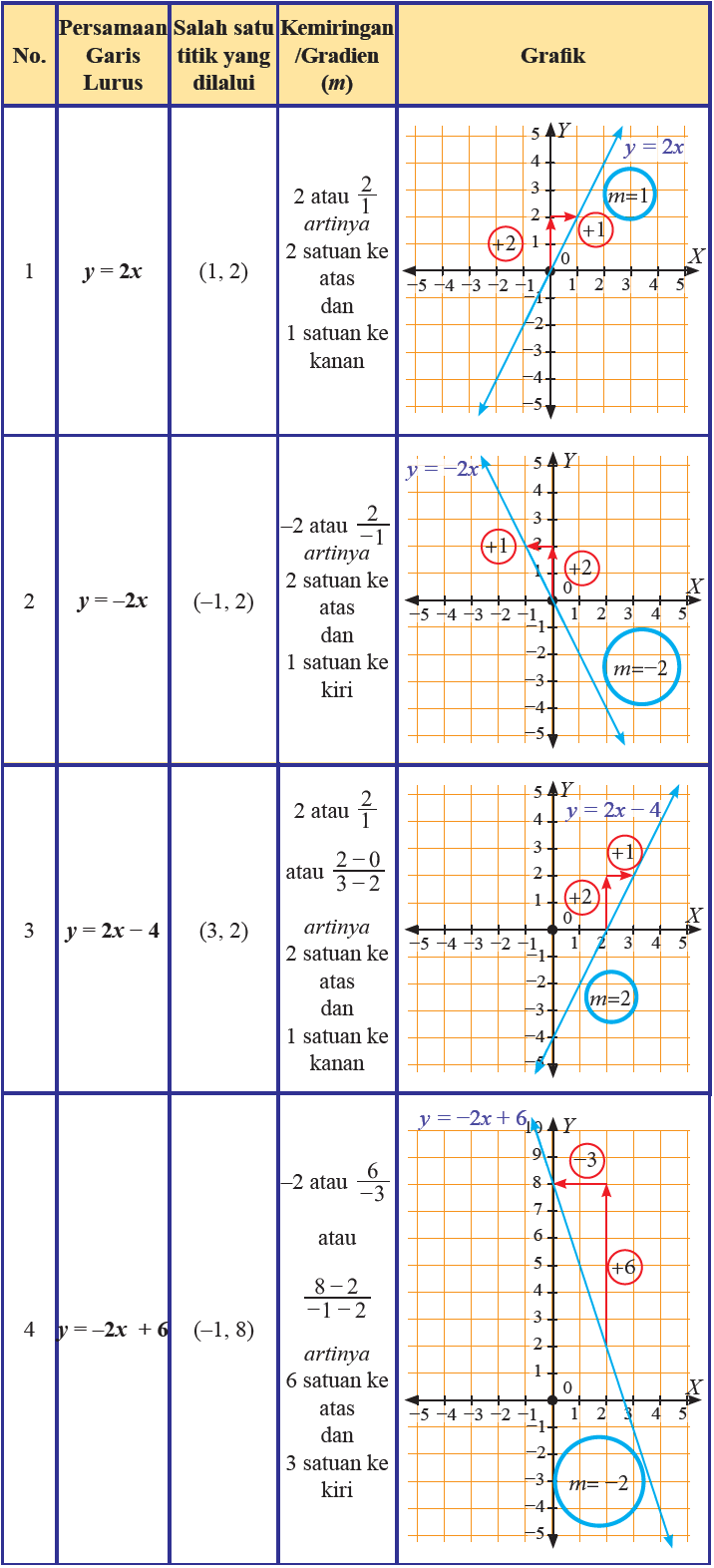
Persamaan garis yang melalui sembarang titik (x1, y1) dan bergradien m adalah y - y1 = m(x – x1)
Bentuk Persamaan Garis Lurus dengan Kemiringan m dan Melalui Titik (x1, y1)

Ayo amati beberapa bentuk persamaan garis lurus yang melalui dua titik dengan kemiringan tertentu pada tabel berikut.
Tabel Bentuk persamaan garis lurus
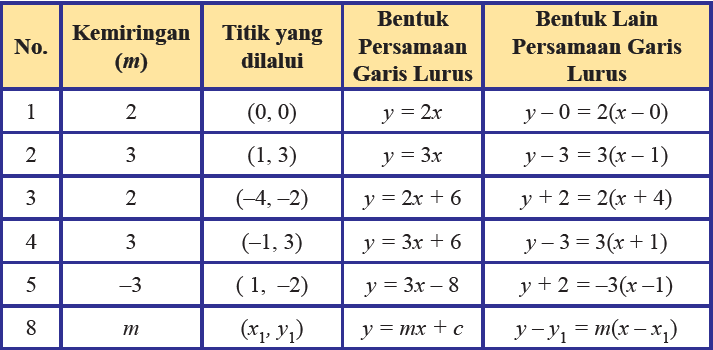
Untuk lebih memahami tentang bentuk persamaan garis lurus dengan kemiringan m dan melalui titik (x1, y1), mari kita simak contoh soal dibawah ini
Contoh Soal :
Tentukan kemiringan garis yang melalui titik A(2, 1) dan B(4, 5).
Penyelesaian :
Misal (2, 1) adalah (x1, y1) dan (4, 5)adalah (x2, y2).
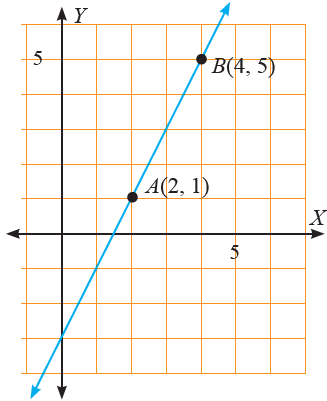
Gambar Garis yang kemiringannya bernilai positif

Perhatikan bahwa kemiringan garis yang bernilai positif, bentuk garisnya naik (selalu miring ke kanan).
1.
Kerjakan soal dibawah ini dengan benar!
Gradien garis dengan persamaan 3x-5y+15 =0 yaitu ...
A. 5/3
B. 3/5
C. -3/5
D. -5/3
JAWABAN BENAR
B.
3/5
PEMBAHASAN
3x-5y+15 = 0
– 5y = -3x – 15 dikali (-1)
5y = 3x + 15
y = 3/5 x + 3
Gradien (m) = 3/5
2.
Kerjakan soal dibawah ini dengan benar!
Persamaan garis yang sejajar dengan garis 2x+3y+6 = 0 serta melalui titik (-2,5) adalah …
A. 2x+3y-4 = 0
B. 2x-2y+16 = 0
C. 3y+2x-11 = 0
D. 3y-2x-19 = 0
JAWABAN BENAR
C.
3y+2x-11 = 0
PEMBAHASAN
Persamaan garis yang sejajar dengan 2x+3y+6 = 0 artinya gradien garisnya sama. Maka kita tentukan dahulu gradiennya sebagai berikut.
2x+3y+6 = 0
3y = -2x – 6
y = -2/3 x – 2
maka gradiennya = -2/3
sehingga persamaan garis tersebut secara umum adalah y = -2/3x+c
Karena garis tersebut melalui titik (-2,5), maka titik tersebut kita substitusikan pada persamaan untuk mendapat nilai c.
y = -2/3x + c
5 = -2/3 (-2) + c
5 = 4/3 + c
c = 5 – 4/3
c = 15/3 -4/3
c = 11/3
Jadi persamaan garisnya adalah
y = -2/3x + c
y = -2/3 x + 11/3
3y = -2x + 11
3y + 2x – 11 = 0
3.
Kerjakan soal dibawah ini dengan benar!
Gradien dari garis 2y + 4x = 8 adalah......
A. -2
B. 1
C. 2
D. 3
JAWABAN BENAR
A.
-2
PEMBAHASAN
Persamaan garis 2y + 4x = 8 diubah bentuk ke persamaan y= mx+c, maka
y = mx + c
2y + 4x = 8
2y = -4x + 8
y = -4x/2 + 8/2
y = -2x + 4
jadi gradien nya adalah -2 ( A )
4.
Kerjakan soal dibawah ini dengan benar!
Gradien dari persamaan garis yang melalui titik (3, 6) dan (6, 9) adalah.......
A. -2
B. 1
C. 2
D. 3
JAWABAN BENAR
D.
3
PEMBAHASAN
Gradien garis yang melalui titik (x1, y1) dan (x2, y2) , menggunakan rumus :
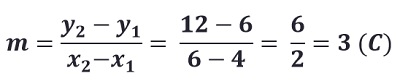

Oops!!!
Yah, jawaban kamu meleset nih. Ingin melihat pembahasan soal ini?

BENAR!!!
Selamat!
Jawaban kamu benar. Ingin lihat pembahasan soal ini?
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved

