APSiswaNavbarV2

redesain-navbar Portlet

BelajarPintarV3

Matematika IPA

Turunan

Daftar Materi

MATERI

Garis Singgung

Amati gambar tersebut, misalkan A adalah suatu titik tetap pada grafik y = f(x) dan B adalah sebuah titik berdekatan yang dapat dipindah-pindahkan sepanjang grafik y = f(x). Misalkan, titik A berkoordinat (a, f(a)) maka titik B berkoordinat (a + x, f(a + 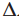x)). Garis yang melalui A dan B mempunyai gradien (kemiringan) . Garis ini memotong grafik di dua titik A dan B yang berbeda.

Jika titik B bergerak sepanjang kurva y = f(x) mendekati titik A maka nilai 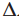x semakin kecil. Jika nilai 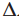x mendekati nol maka titik B akan berimpit dengan titik A. Akibatnya, garis singgung (jika tidak tegak lurus pada sumbu-x) adalah garis yang melalui A(a, f(a)) dengan gradien.

Contoh

Perhatikan gambar berikut !

Tentukan gradien garis singgung pada kurva f(x) = x2 di titik dengan absis 2

Jawab : 

Jadi, gradien garis singgung kurva f(x) = x2 di titik dengan absis x = 2 adalah m = 4.

Turunan fungsi di x = a

Jika fungsi y = f(x) terdefinisi di sekitar x = a maka:

 

Jika  ada maka nilainya disebut turunan fungsi f(x) di x = a. Turunan fungsi f ialah suatu fungsi juga, yaitu fungsi turunan yang dilambangkan dengan f '(x). Untuk menyatakan turunan di x = a dinyatakan dengan f '(a). Jadi,

Contoh

Gunakan konsep limit untuk menyelesaikan soal berikut ini.

Jika f (x) = x2 – x , tentukan f'(5) ! 

Jawab :

 

Jadi sudah paham kan kalau materi turunan sebenarnya berasal dari konsep limit pada materi sebelumnya 

Yuk, lanjut lagi ke materi konsep turunan berikutnya ..

Mengenal Notasi Leibnitz

Sobat pintar telah mempelajari bahwa turunan fungsi f(x) dinotasikan dengan f '(x). Nilai 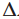x menyatakan perubahan nilai x, yaitu 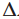x = x2 - x1. Adapun perubahan f(x + 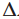x) - f(x) menyatakan perubahan nilai fungsi f(x) dinotasikan dengan 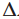f. 

Selanjutnya, bentuk limit tersebut dapat dituliskan menjadi 

Selain itu, terdapat notasi lain untuk menyatakan turunan fungsi, yaitu . Diketahui fungsi 

............... (1) 

Sehingga turunan fungsi (1) menjadi 

Notasi tersebut diperkenalkan oleh seorang ahli matematika Jerman, yaitu Gottfried Wilhelm Leibnitz (1646–1716) sehingga dinamakan notasi Leibnitz, tepatnya notasi Double d Leibnitz.

Contoh 

Misalkan f(x) = x3, tentukanlah .

Jawab :

 

Nah, bagaimana sobat pintar .. sudah paham kan mengenai konsep turunan ? 

Lanjut lagi ya belajarnya 

 

redesain-navbar Portlet