Matematika IPA

Menentukan Turunan Fungsi f(x)=axn dengan n Bilangan Rasional

Misalkan, fungsi f(x) = x^1/2, maka turunan fungsi f(x) adalah 

Dari uraian tersebut dapatkah sobat pintar menduga bentuk umum turunan fungsi f(x) = axⁿ?

Cobalah nyatakan bentuk tersebut dengan kata-kata sobat sendiri. Konsep turunan fungsi f(x) = axⁿ yang telah sobat pelajari tersebut memperjelas kesimpulan berikut :

Contoh

Tentukan Turunan Fungsi-fungsi Berikut !

a. 

b. 

Jawab :

a. 

b. 

Yuk, lanjut ke materi berikutnya...

Turunan Fungsi Berbentuk y = u + v

Diketahui, fungsi y = f(x) dengan f(x) = u(x) + v(x), dalam hal ini u(x) dan v(x) fungsi yang dapat diturunkan di x = a untuk a bilangan real. Dengan demikian, 

Dari uraian tersebut, dapatkah sobat pintar menduga bentuk umum turunan fungsi y = u  v ?

Cobalah nyatakan bentuk tersebut dengan kata-kata sobat sendiri. Konsep turunan fungsi y = u  v yang telah sobat pelajari tersebut memperjelas kesimpulan berikut :

Contoh

Tentukan turunan fungsi berikut !

a. f (x) = x³ – 3x²

b. 

Jawab :

a. f(x) = x³ – 3x² maka f '(x) = 3x² – 6x

b. 3 - 

Turunan Fungsi y = c.u

Jika diketahui, fungsi y = f(x) dengan f(x) = c . u(x), dalam hal ini c konstanta dan u(x) fungsi yang dapat diturunkan di x = a untuk a bilangan real sehingga ,

Misalkan, a adalah sebarang bilangan real sehingga untuk y = f(a) = c . u(a) berlaku f '(a) = c . u'(a). Akibatnya, dari y = cu berlaku y' = c . u'

Contoh 

Tentukan Turunan Fungsi Berikut !

a. f(x) = 3x²

b. 

Jawab :

a. f(x) = 3x² maka f '(x) = 6x

b. 

Bagaimana sobat pintar.. masih semangat kan belajarnya,

yuk lanjut lagi!

Turunan Fungsi y = uv

Diketahui, fungsi y = f(x) dengan f(x) = u(x) · v(x), dengan u(x) dan v(x) adalah fungsi yang dapat diturunkan di x = a, untuk a bilangan real. Oleh karena itu, 

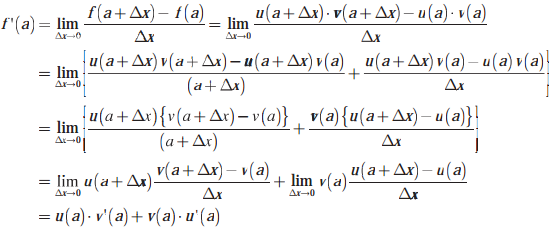
Oleh karena itu, jika y = f(x) = u(x) · v(x) dengan a bilangan real sebarang berlaku f '(a) = u(a) · v'(a) + v(a) · u'(a).

Sehingga,

Untuk y = u · v, maka y' = uv' + vu'.

Contoh

Tentukan turunan fungsi berikut !

a. f(x) = (5x² – 1) (3x – 2)

Jawab :

a. f(x) = (5x² – 1) (3x – 2)

Misalkan, u = 5x² – 1 maka u' = 10x dan v = 3x – 2 maka v' = 3

sehingga

f '(x) = u (x) . v' (x) + v (x) . u' (x) = (5x² – 1) . 3 + (3x – 2) . 10x

= 30x² – 20x + 15x² – 3 = 45x² – 20x – 3

Turunan Fungsi y = u pangkat n

Diketahui y = f(u) dengan f(u) = un dan u = g(x). Jika fungsi u = g(x) dapat diturunkan di x = a, untuk a bilangan real maka 

Oleh karena a bilangan real sebarang maka, 

Dengan cara yang sama, dapatkah sobat pintar memperoleh  ? 

Untuk 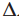x mendekati nol maka 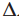u mendekati nol, sehingga 

f(f u) = un, f '(u) = nu^{n – 1} sehingga y'(x) = nu^{n – 1} u'(x).

Jadi, disimpulkan bahwa Untuk y = un maka y' = nu^{n – 1} u'(x).

Contoh

Tentukan Turunan Fungsi Berikut !

a. f(x) = (2 + 3x²)⁹

Jawab :

a. f(x) = (2 + 3x²)⁹

Misalkan, u = 2 + 3x² maka u’(x) = 6x sehingga

f (x) = u⁹

f ‘(x) = 9u⁸ .u’(x) = 9(2 + 3x²)8.6x = 54x(2 + 3x²)⁸

Aturan Rantai

Coba sibat pintar perhatikan kembali uraian materi tentang fungsi y = uⁿ . Dari uraian tersebut, diperoleh bahwa untuk y = f(u) = uⁿ dengan u = g(x) maka turunannya y' = nu^n–1 u'(x). Hasil tersebut menggambarkan aturan rantai.

Amati contoh soal berikut

Contoh

Tentukan Turunan Fungsi 

Jawab :

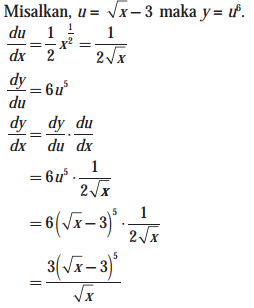
Ayo lanjut lagi ke materi berikutnya..,

Turunan Fungsi y = u/v

Diketahui, fungsi y = f(x) dengan , dalam hal ini u(x) dan v(x) fungsi yang dapat diturunkan di x = a untuk a bilangan real maka, 

Oleh karena itu, jika y =  dengan a sebarang bilangan real sehingga berlaku 

maka . 

Kesimpulan :

Untuk , berlaku 

Contoh

Tentukan Turunan Fungsi f(x) = tan x

Jawab :

f(x) = tan x = 

Misalkan u = sin x maka u' = cos x dan v = cos x maka v' = – sin x.

= sec²x

Nah, bagaimana sobat pintar apakah sudah paham semua materi tentang cara menentukan turunan fungsi ?

Jika masih bingung bisa mengunakan fitur diskusi ya..,

Selamat balajar